什么是AMC

AMC(American Mathematics Competition) 是美国的数学竞赛，分为AMC8、AMC10/12、AIME、USAMO等等级别

AMC8每年10-1月报名，1月举行，每次40分钟，一共25道选择题，每题1分，不答或答错不得分；

AMC10/12每年6-11月报名，11月举行，每次75分钟，也是25道选择题，每题6分，不答得1.5分，答错0分。

AMC中国赛区采用的是中英文双语试题。

今年AMC8中国区的比赛不接受个人报名，只能通过所在国际学校统一报名或通过机构报名，报名费120元。AMC8的报名要求是八年级以下(年龄限制)，国内现状是一般四年级就可以参加了。我也是最近才接触到，因此找了今年AMC8的真题给四年级的Oscar同学试一下，40分钟做了13题，对了10题。（文末「阅读原文」可下载）。

2023年AMC8真题解析

第一题非常简单，基本的运算：

(8×4+2)-(8+4×2)=34-16=18，选D

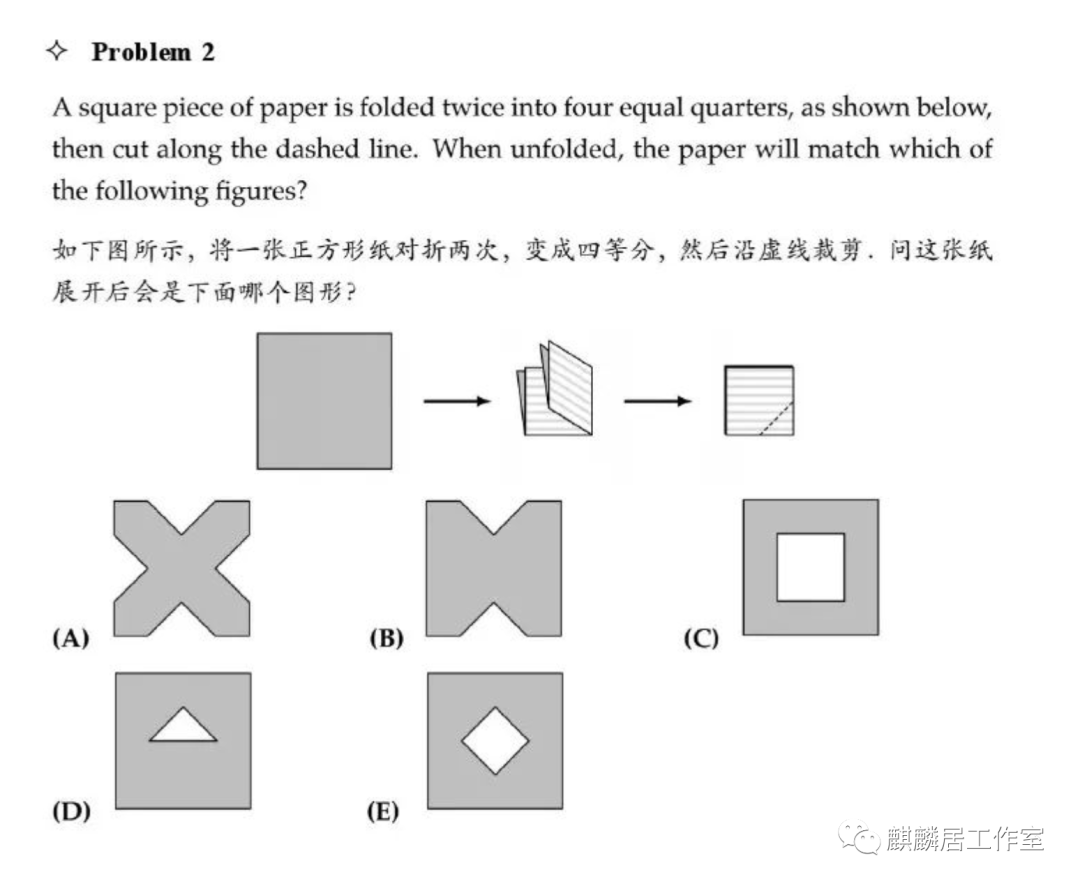
第二题也不难，根据折叠方向，裁剪掉的图形应该在正方形中心，且与正方形的边成45度角，选E

第三题看着很长一段，但其实仔细看就是一个公式的应用，直接把数据代入进去36-0.7×18=36-12.6=23.4，选B

第四题有两种方法，一种是直接沿着格子把数字一格格填进去，可以得到阴影方格的四个数；

另一种是进行一些计算：首先根据规律知道2下方的数字应该是9=3×3；而9右下方的格子应该是5×5=25，因此1下方的阴影格子就是23，而4左上方的格子是4×4=16，于是6左边的阴影格子是19；同理，9右下方的格子是7×7=49，2下方的阴影就是47；而16左上方的格子是6×6=36，所以5左边的阴影就是39；

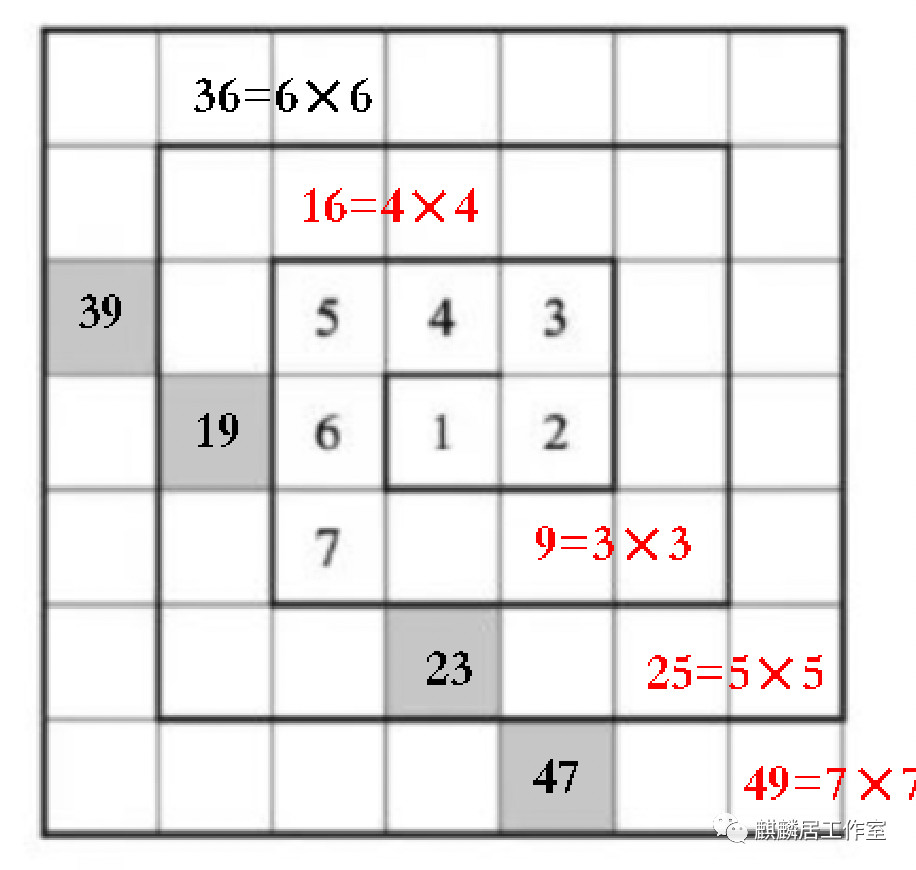
因此四个数就是19，23，39，47，其中39是合数，其他三个都是质数，选D。（建议把100以内的质数都熟悉一下）

第五题主要考察采样统计的思路，如果没有接触过这方面可能有点陌生，但只要接触过我相信也不难。因为180条鱼中有30条是鳟鱼，所以可以认为鳟鱼占全部鱼的1/6，或者全部鱼是鳟鱼数量的6倍。

250*(180/30)=250*6=1500条。选B。

第六题涉及幂运算，需要提前了解这个知识点。

解题的关键点在于有一个0，0如果在底数上，则无论指数(>0时)是多少，结果都是0；而如果乘数有一个0，积就为0；所以0必须放在指数上。

当0在指数上时，底数只要不为0，结果都是1，于是底数上的数就被“浪费”掉了，当然用比较小的2放在底数，这样剩下2和3最大的是3²=9。

即2⁰×3²=9，因此选C。

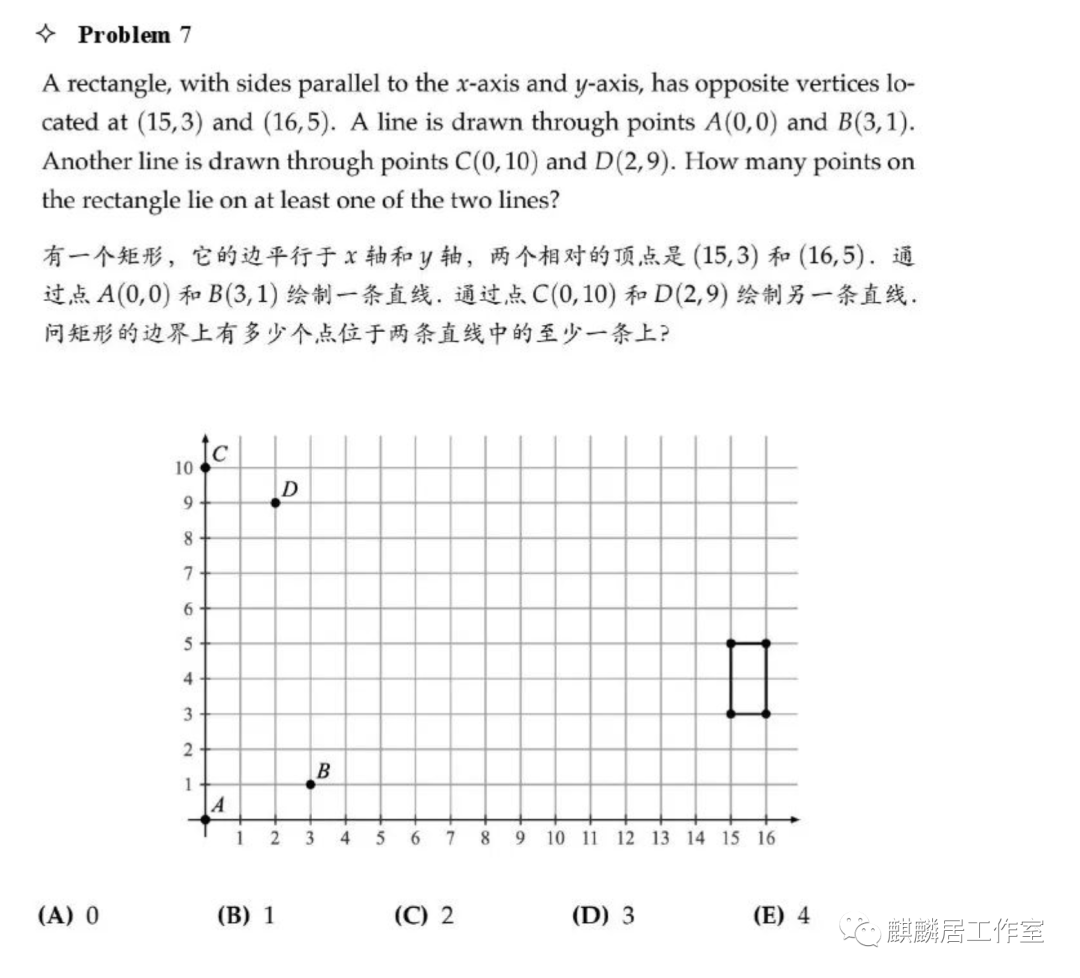
第七题也可以用直接画线来看图的方式快速解，

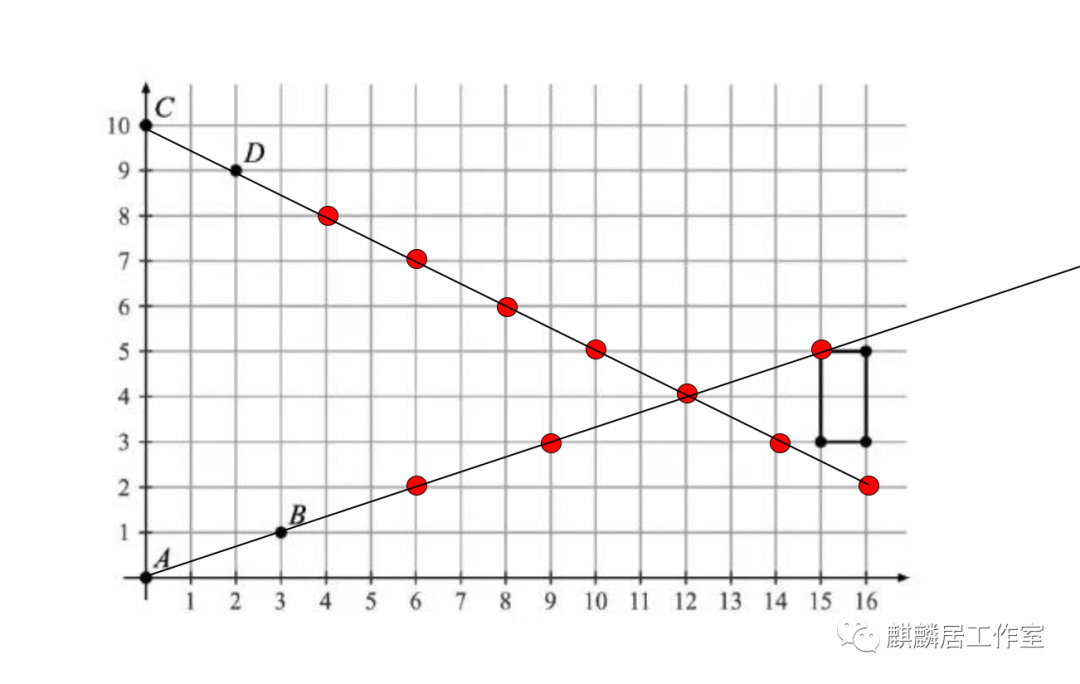
根据规律，沿AB直线每横向移动3格纵向会移动1格，沿CD直线每横向移动2格纵向会移动1格，因此红点的位置就是直线上的点，可以清楚看到只有一个点会出现在AB和CD上，选B。

第八题只要意识到每一场球赛一方胜一方负，于是每一列都是2个1、2个0，直接可以得出Tiyo的结果是000101，选A。

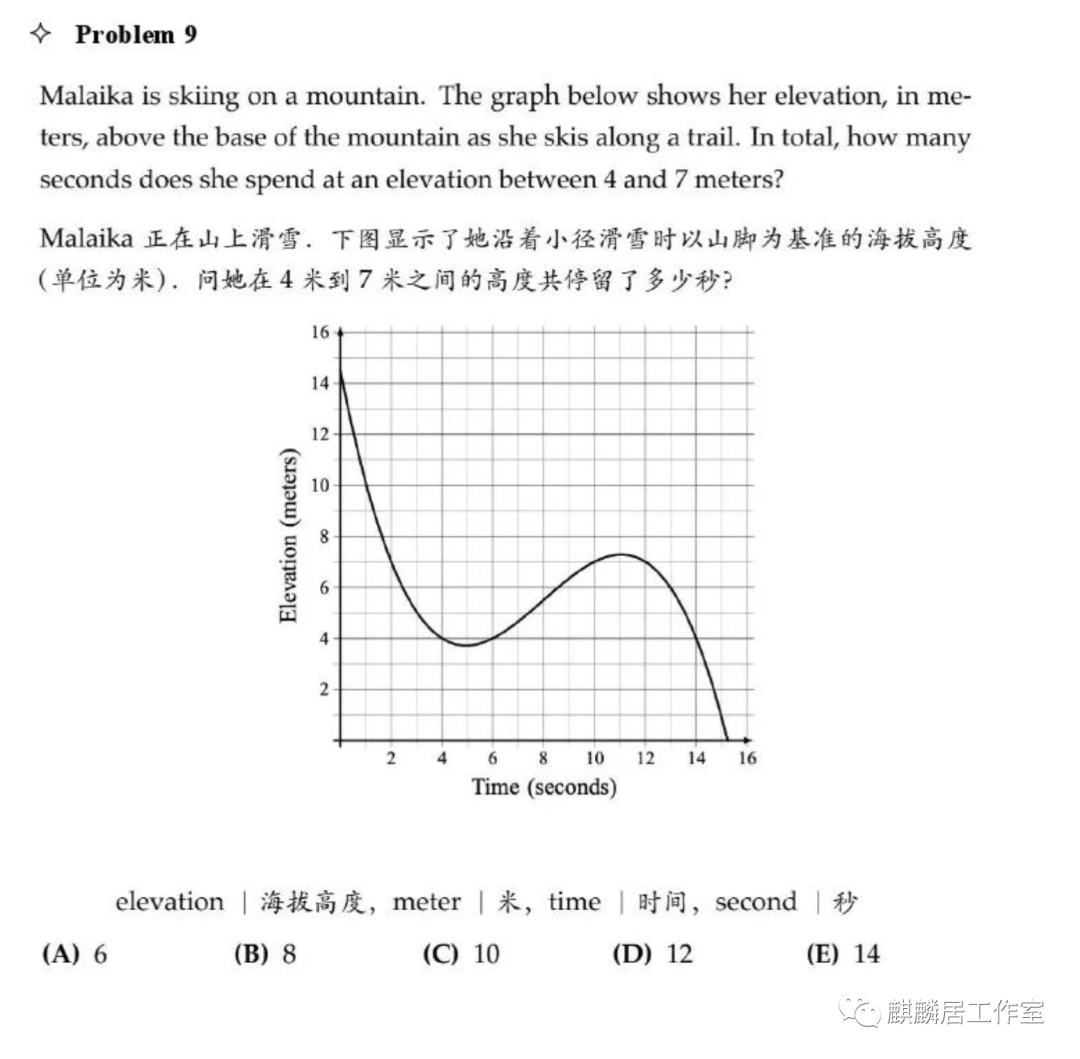
第九题主要是看图和理解“停留”的含义，第一次到7米是第2秒，第一次到4米是第4秒；第4-6秒间在4米以下了，不应该算入停留时间；第6秒又回到了4米，直到第10秒回到了7米；第10-12秒超过7米了，也不应该算入停留时间；第12-14秒再次回到了4-7米的区间。

因此(4-2)+(10-6)+(14-12)=2+4+2=8秒，选B。

第10题通过画流程图就可以轻松得到

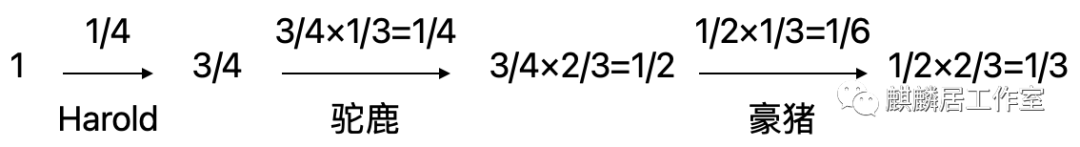
所以剩下1/3，选D。

第11题是一个单位换算，6.5个月大约为6.5*30*24=4800小时，292526838/4800≈300000000/4800=62500英里每小时，选C。

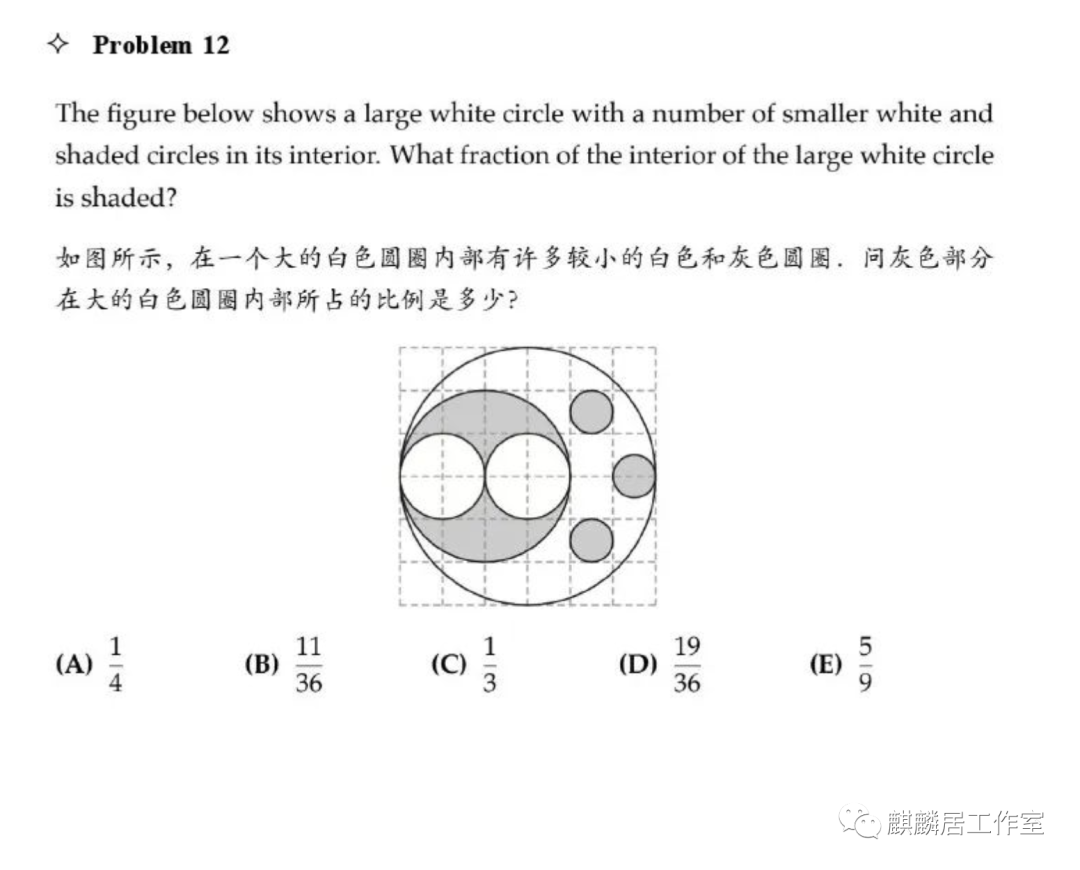
第12题我们可以看出大白色圆圈的直径是6格，大灰色圆圈的直接是4格，小白色圆圈的直径是2格，小灰色圆圈的直径是1格。

我们知道圆的面积是和直径成平方关系的(不知道具体公式πr²也没关系)，因为这里要求的是面积的比例，因此面积之比就等于直径的平方之比。

于是我们直接可以使用直接的平方来代替面积进行计算，大圆的面积是6²=36，阴影部分的面积是4²-2×2²+3×1²=16-8+3=11，所以答案为11/36，选B。

第13题的重点是均匀分布，即7个饮用水补给站将全程平均分为8段，2个维修站将全程平均分为3段。

那么第三个饮用水的位置在3/8全程处，第一个维修站的位置在1/3全程处。

第三个饮用水补给站在第一个维修站后2英里，也就是3/8全程比1/3全程要多2英里，2/(3/8-1/3)=48英里，选D

第14题要求使用的邮票最多，那么尽量用面值小的邮票。$7.10=710美分。

先用5美分的，一共5×20=100美分，剩余610美分

再用10美分的，一共10×20=200美分，剩余410美分

最后再用25美分的，可用410/25=16......10美分，此时一共用了56张邮票，但是金额还差10美分，因为我们把5美分和10美分都用完了，我们需要腾出一张10美分的来：

拿1张25美分换回2张10美分和1张5美分，然后再把10美分的贴上，于是我们使用了56+1-3+1=55张。验算一下：

5×19+10×19+25×17=710美分，19+19+17=55张，选E。

第15题，他绕行时已经走了5个街区，还需要走5个街区，即时间是5分钟。现在他需要多走3-1=2个街区，即一共需要走7个街区，所以每个街区需要用5/7分钟。10个街区一共半英里，即每个街区1/20英里，速度=(1/20)/(5/7)*60=21/5=4.2英里/小时，选B。

第16题，通过观察，最下面一行是按照PQR的顺序，由于20÷3=6......2，因此最下面一行会有7个P、7个Q、6个R

同理倒数第二行会有7个Q、7个R、6个P，倒数第三行会有7个R、7个P、6个Q；三行一共有20个P、20个Q、20个R；以三行为一组，20行其实是重复了6次再多出最后两行。即P的个数为20×6+7+6=133，Q的个数为20×6+7+7=134，R的个数为20×6+6+7=133，选C。

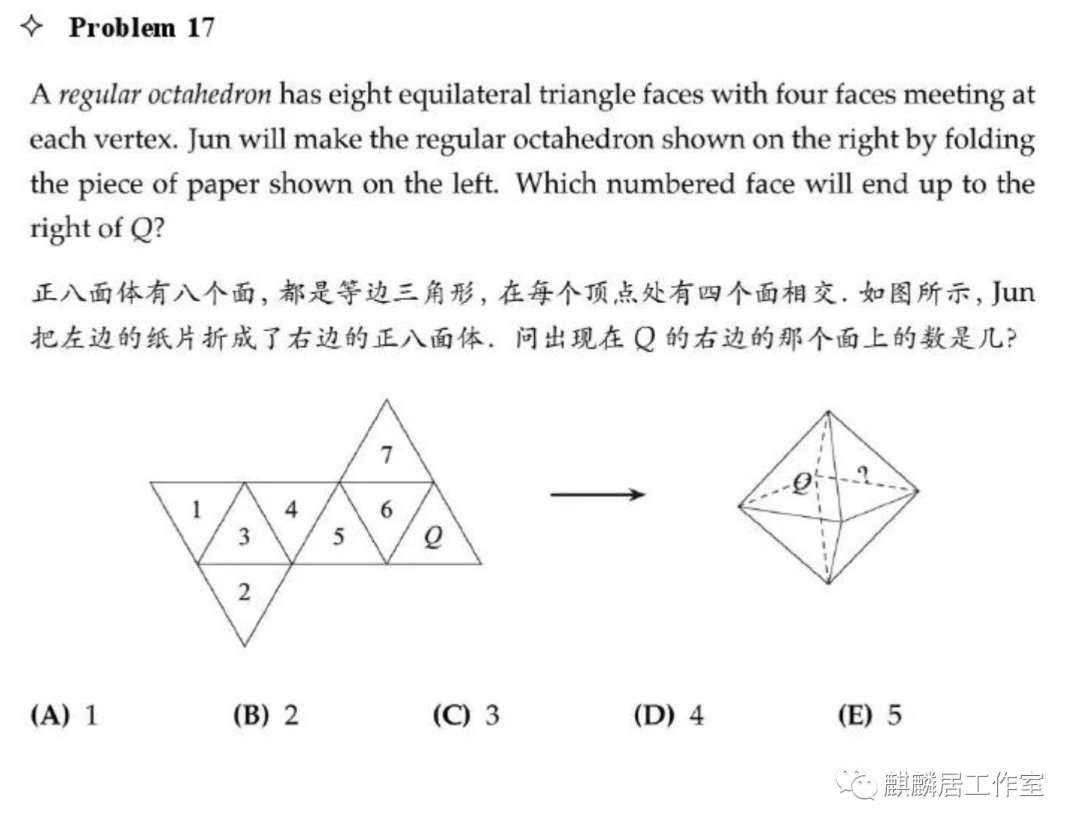
第17题考察空间想象能力

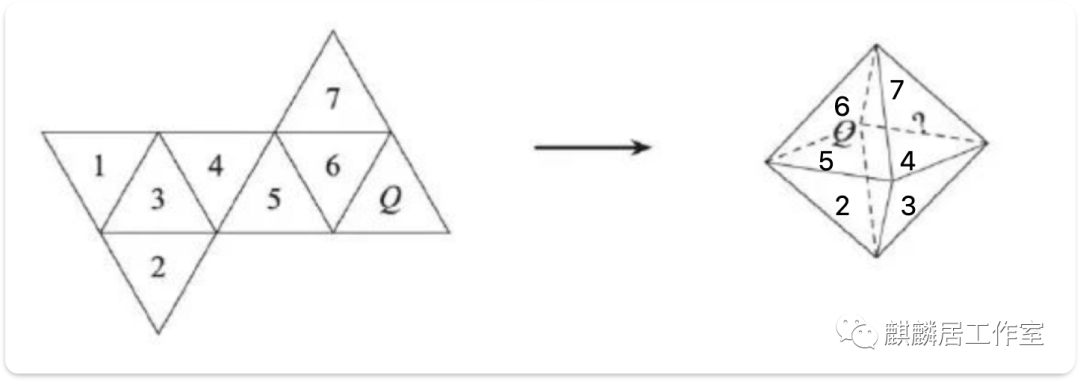
问号处应为1，选A。

第18题求最少跳多少次，因此应该尽量先向右跳，2020/5=404次跳到第2020片的位置，

此时可以直接硬算：第405次再往右跳就超过了2023片到达了2025片，这时第406次再往回跳到达2022片，第407次再往右跳达到了2027片，第408次往左到2024片，第409次再往左到2021片，第410次再往右到2026片，第411次再往左到2023片，因此选D。

也可以思考：向右1次向左1次是+2，向右1次向左2次是-1；我们需要用+2和-1来凑出一个3 (2023-2020=3)，那么很明显2×2-1=3，所以我们进行两次（向右1次向左1次）和1次（向右1次向左2次），即404+2×2+1×3=411，选D

第19题，也是一个面积和边长的比例关系，面积比=边长比的平方。内部三角形边长是2/3，面积就是4/9，那么三个梯形的面积之和就是5/9，一个梯形就是5/27，(5/27)/(4/9)=5/12，选C。

第20题涉及到几个统计学的概念，如果没有接触过可能没法做。极差=最大值-最小值，众数表示出现次数最多的数，中位数表示在最中间的数。

目前的5个数极差=28-3=25，众数是3，中位数是8。

要使极差变为25×2=50，众数和中位数不便，很显然要在8的左边和右边各加上一个数，并且不能是8、11、28中的一个。

为了和最大，我们应该尽量加较大的数，因此8右边的数应该用3+25×2=53，保证极差=50；而8左边应该尽可能靠近8，选择7

所以53+7=60，选D。

第21题，我们先求出数字总和为1+2+…+9=45，每组的卡片数字和为15，

我们再列出三个1-9之间不同数相加得到15的方案：

1+5+9、1+6+8

2+4+9、2+5+8、2+6+7

3+4+8、3+5+7

4+5+6

一共10组；1的分组方案只在第一行，因此第一行必选1个；而2的分组方案只在第二行，第二行也必选1个：

如果第一行选1+5+9，则第二行只能选2+6+7，剩下3+4+8

如果第一行选1+6+8，则第二行只能选2+4+9，剩下3+5+7

因此只有2种分组，选C。

第22题，我们假设第一项为a，第二项为b，那么第三项是a×b，第四项是a×b²，第五项是a²×b³，第六项是a³×b⁵。

我们把4000进行质因数分解：4000=2⁵×5³，很明显a=5，b=2，选D。

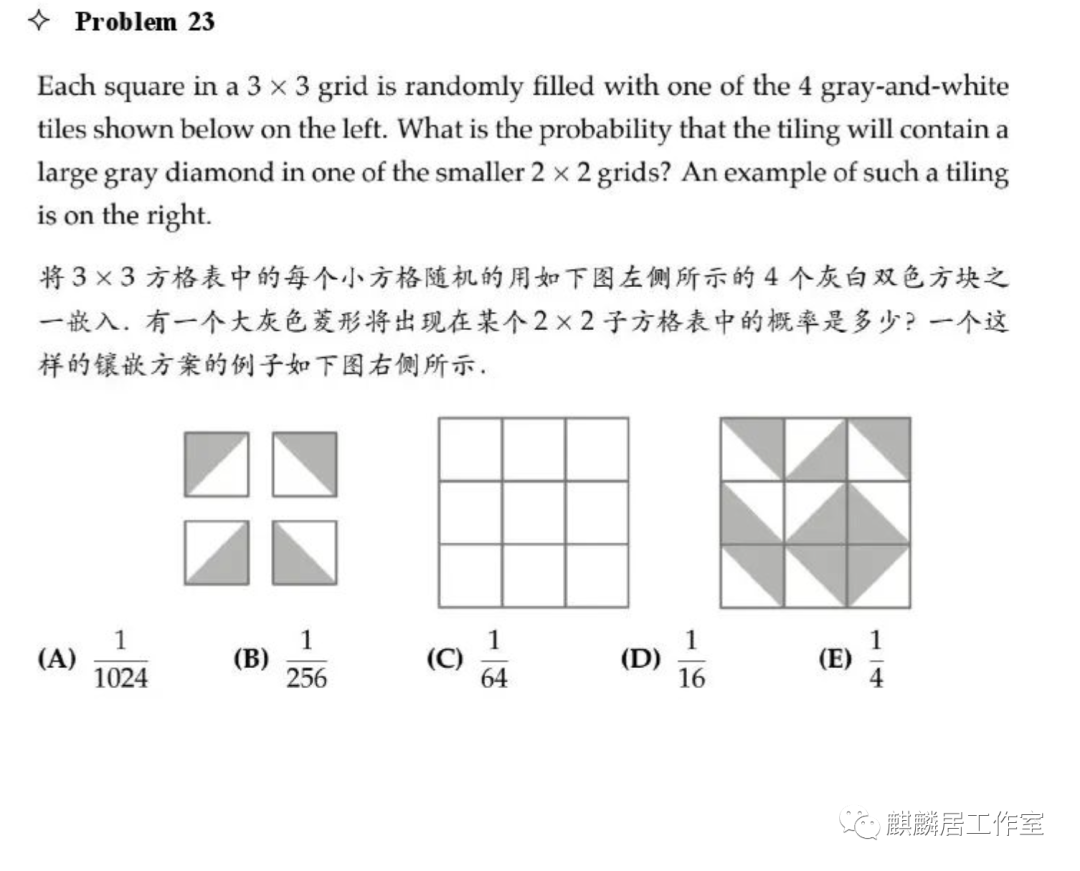
第23题有两种方法：第一种方法，我们考虑到有四种可能的灰色菱形，即左上左下右上右下，每一种出现的概率都是1/4×1/4×1/4×1/4=1/256，因此一共4×1/256=1/64。

第二种方法，我们先考虑中间的格子，无论中间格子的方向是怎样，我们都可以确定一个角落来组成灰色菱形，并且其他三个角落都无法组成灰色菱形。

因此当中间格子确定之后，目标角落的剩余三个概率为1/4×1/4×1/4=1/64，选C。

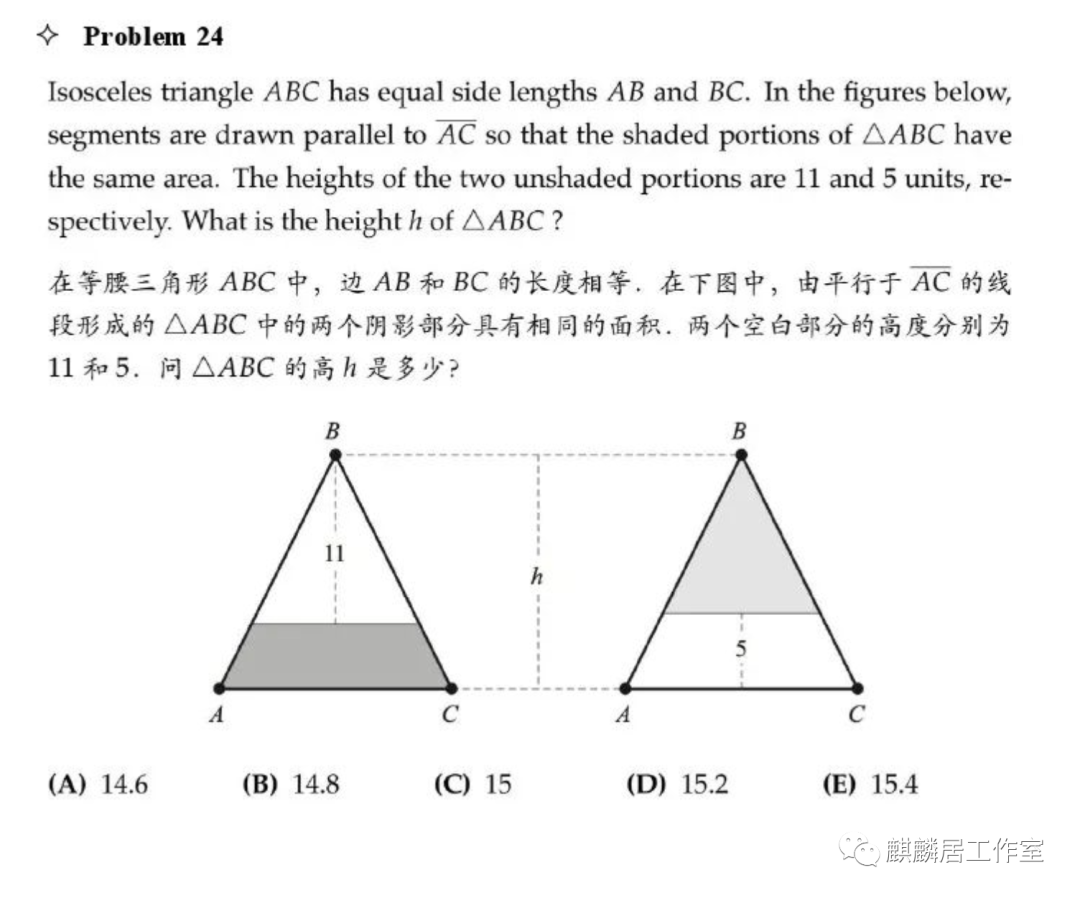
第24题还是一个面积比=边长比的平方的问题，

左边图阴影/△ABC=1-(11/h)²，右边图阴影/△ABC=((h-5)/h)²

1-(11/h)²=(h-5/h)²，解方程，这里是一个一元二次方程，比较复杂：

两边打开1-121/h²=(h-5)²/h²，两边同时乘上h²：h²-121=h²-10h+25，

整理得到10h=146，h=14.6，选A

最后一题，是一个等差数列，

1<=a₁<=10，13<=a₁+d<=20，241<=a₁+14d<=250

由1式、3式得到231<=14d<=249，16.5<=d<=17.7，即d=17

所以241<=a₁+238<=250，这就要求3<=a₁<=10；

而13<=a₁+17<=20要求a₁<=3，所以a₁=3，a₁₄=3+13×17=224，2+2+4=8，选A。

答案汇总：

DEBDB CBABD CBDEB CADCD CDCAA