第一部分：试题

1、少年+科技+创新+能力=314，其中不同的汉字表示不同的非0数字，则分数（少+科+创+能）/（年+技+新+力）的值是多少？

2、把一笔奖金分给甲乙两个组，平均每人可得到600元；如果只分给甲组，平均每人可得到1000元；如果只分给乙组，平均每人可得多少元？

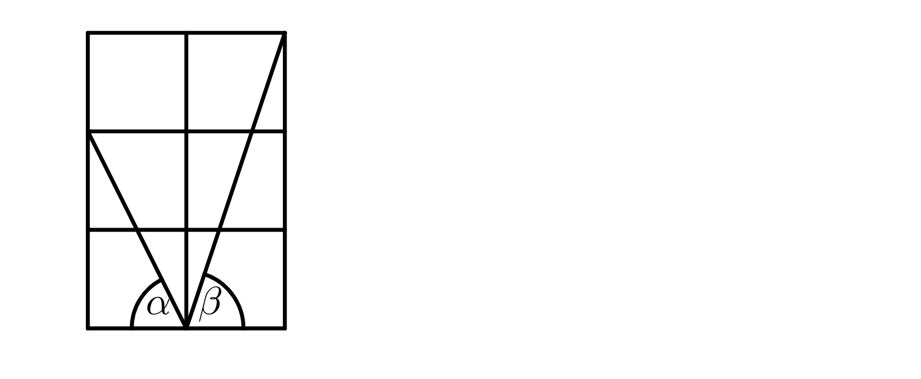
3、如图所示的6个单位正方形组成的2×3矩形中，标示出两个角α和β，则α+β的度数是？

4、从十个数1、2、3、4、5、6、7、8、9、10中去掉一个数，使得剩下的九个数可分为两组，且这两组数的乘积相等．则去掉的数是？

5、五个不同的自然数，两两之和依次等于3、4、5、6、7、8、11、12、13、15这10个值，则这五个自然数的平均数是？

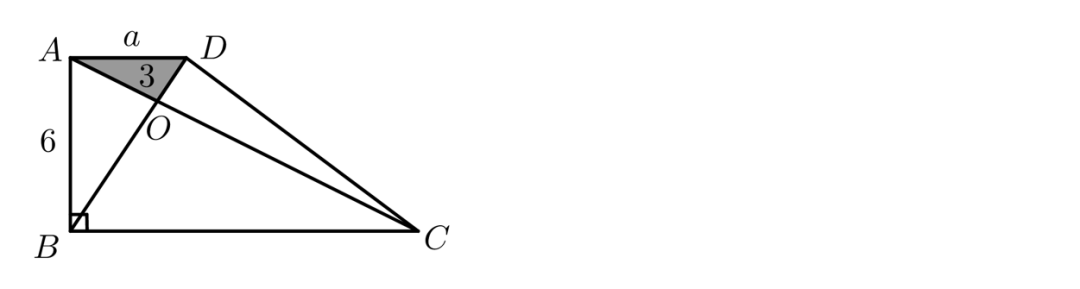
6、梯形ABCD中，AD∥BC，∠ABC=90°。对角线AC与BD相交于O点，且AB=6厘米，BO=3DO，三角形AOD的面积为3平方厘米。则梯形ABCD的周长为多少厘米？

7、从28个自然数1、2、3、…、28中任取n个数，使得其中必有2个数的差是7，则n的最小值是？

8、核研所每天按时出车沿规定路线定时到达A站，接上同时到达A站的专家准时到达核研所．有一天，该专家提前55分钟到达A站，因接他的车还没来，他就步行向核研所走去．在途中遇到接他的汽车，立即乘上车，这样比通常提前10分钟到达核研所．则汽车速度是专家步行速度的多少倍？

9、一个长方体的棱长都是质数，其中相邻的两个表面长方形的面积之和是209平方厘米，则这个长方体的体积是多少立方厘米？

10、设a、b、c、d是1-9之间的四个不同数字，用这四个数字（不能重复）可以组成很多不同的四位数，小明把所有可能组成的四位数加起来，但他不小心把其中一个四位数多加了一遍，结果为128313，那么，正确的结果应该是？

二、解答题（满分60分，11-13题各10分，14/15题各15分）

11、计算：(43/9－0.8＋29/9)×[(37/5＋2.6) ×1.25]

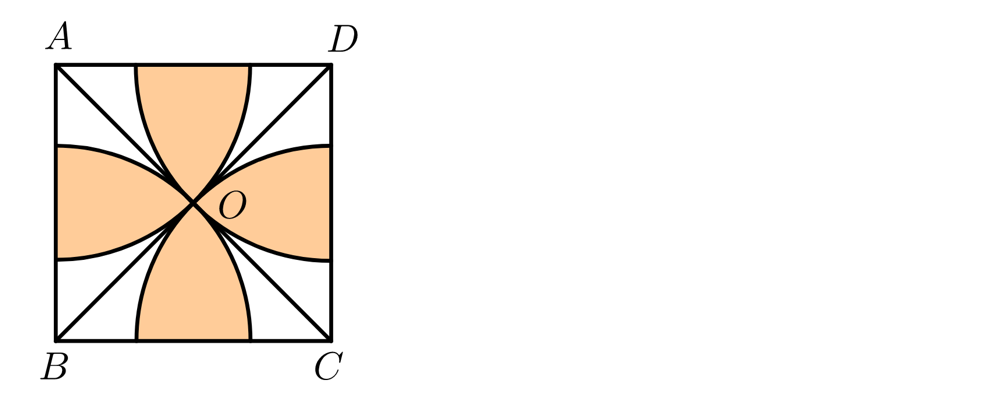
12、正方形ABCD的面积等于8平方厘米，它的对角线交点为O，分别以A、B、C、D为圆心画过O点的四条圆弧，如图所示，图中四个花瓣形（阴影部分）的总面积是多少平方厘米？（圆周率=3.14）。

13、如图是一个边长为100米的正方形跑道ABCD，甲、乙两人同时分别从A、C两点出发，沿着跑道顺时针方向出发，甲的速度为每秒7米，乙的速度为每秒5米，他们每到转弯处都要停留5秒钟，请问，当甲第一次追上乙时，要用多少时间？

14、四只容量相同且有刻度的玻璃杯，其中三只分别装满三种不同的果汁，另外一只为空杯。你可以利用这只空杯，怎样操作得到三杯成分相同的混合果汁？如果增加一个同容量，而且装满与以上三种不相同的饮料的玻璃杯，你又怎样操作得到四杯成分相同的混合果汁？

15、阅读以下材料：如图所示，长方形ABCD中，AB=a，AD=b，分割成四个小长方形，其中AG=a-1，AE=b-1。由于S(ABCD)=S(AEPG)+ S(EFCD)+S(BCHG)-S(PFCH)，即ab=(a-1)(b-1)+a+b-1,(a-1)(b-1)=ab-a-b+1。

运用上述公式，解决以下问题：

一个数，其所有位数上的非零数字之积恰好等于这些数字之和，这样的数称为“鹏程数”，例如:80000、11125都是五位数的“鹏程数”。

特别地，我们把各个数字均不为零的“鹏程数”叫作“真鹏程数”。

(1)求出所有三位“鹏程数”之和

(2)求出四位“真鹏程数”的四个数字

第二部分：解析

同2018年第一题。考虑十位取9+8+7+6=30，个位取5+4+3+2=14，可以满足题意且为唯一情况，算式值为15/7。

列方程解题，设甲组x人，乙组y人。有600(x+y)=1000x，x/y=3/2，1000x/y=1500（元）。

3、如图所示的6个单位正方形组成的2×3矩形中，标示出两个角α和β，则α+β的度数是？

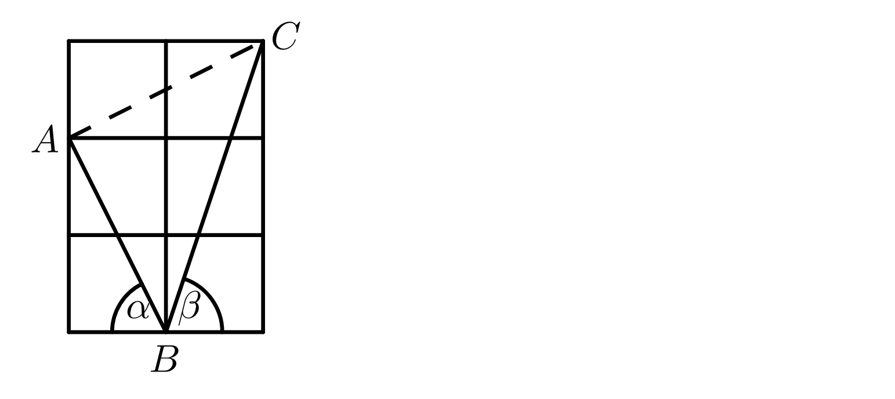
将1-10分解质因数后，发现仅有7为单独的质因数，去掉的数是7。

五个不同自然数两两相加，每个数用到4次，即3+4+5+6+7+8+11+12+13+15=84=五数和的4倍。这五个自然数的平均数=84÷4÷5=4.2。

6、梯形ABCD中，AD∥BC，∠ABC=90°。对角线AC与BD相交于O点，且AB=6厘米，BO=3DO，三角形AOD的面积为3平方厘米。则梯形ABCD的周长为多少厘米？

根据共边定理，S△ABD=4S△AOD=12，解得a=4；另根据风筝模型，知道S△BCD=3S△ABD=36，S△DHC=24，HC=8，根据勾股定理可知DC=10，梯形ABCD的周长为6+4+10+4+8=32厘米。

汽车比平时提前10分钟到达核研所，因为它没有走A站到与专家相遇点的路程。可知，A站到相遇点汽车单程用5分钟。也就是说，汽车比平时早5分钟接到专家，专家共走了55-5=50分钟。汽车速度是步行速度的10倍。

10、设a、b、c、d是1-9之间的四个不同数字，用这四个数字（不能重复）可以组成很多不同的四位数，小明把所有可能组成的四位数加起来，但他不小心把其中一个四位数多加了一遍，结果为128313，那么，正确的结果应该是？

用a、b、c、d这四个数字可以组成24（4×3×2×1）个不同的四位数，并且a、b、c、d在个位、十位、百位、千位各出现6次．所以这24个不同的四位数的和为：

代入检验，当a+b+c+d=19时，余数1659各位相加=21，不符合题意。当a+b+c+d=18时，余数8325各位相加=18。得正确结果是18×6666=119988。

二、解答题（满分60分，11-13题各10分，14/15题各15分）

11、计算：(43/9－0.8＋29/9)×[(37/5＋2.6) ×1.25]

12、正方形ABCD的面积等于8平方厘米，它的对角线交点为O，分别以A、B、C、D为圆心画过O点的四条圆弧，如图所示，图中四个花瓣形（阴影部分）的总面积是多少平方厘米？（圆周率=3.14）。

13、如图是一个边长为100米的正方形跑道ABCD，甲、乙两人同时分别从A、C两点出发，沿着跑道顺时针方向出发，甲的速度为每秒7米，乙的速度为每秒5米，他们每到转弯处都要停留5秒钟，请问，当甲第一次追上乙时，要用多少时间？

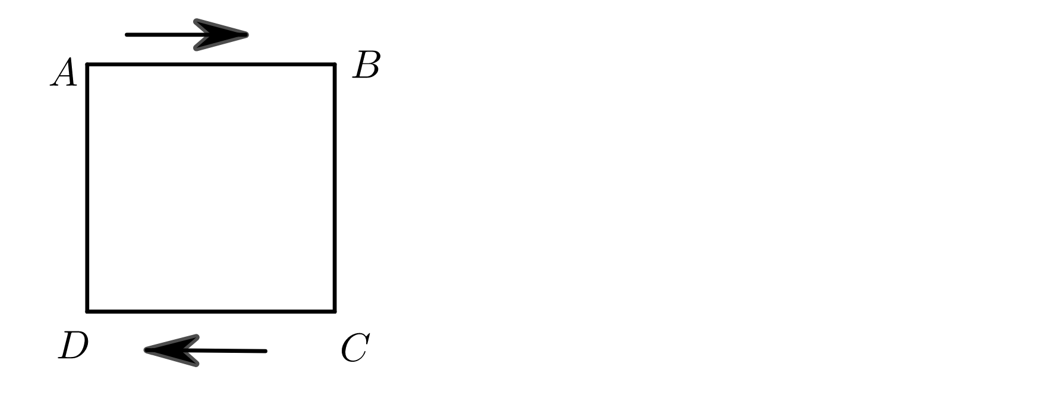
n=8时，甲刚好跑了800米，即2圈，刚好回到A点，这时甲共用800/7+5×7=149+2/7(秒)，而乙经过一圈半到达A点的时间是600/5+5×5=145秒，与甲到达A的时间相差不到5秒，即甲到达A点时，乙还未离开，甲第一次追上乙，用了149+2/7(秒)。

(1)

(2)

15、阅读以下材料：如图所示，长方形ABCD中，AB=a，AD=b，分割成四个小长方形，其中AG=a-1，AE=b-1。由于S(ABCD)=S(AEPG) +S(EFCD)+S(BCHG)-S(PFCH)，即ab=(a-1)(b-1)+a+b-1,(a-1)(b-1)=ab-a-b+1。

运用上述公式，解决以下问题：

一个数，其所有位数上的非零数字之积恰好等于这些数字之和，这样的数称为“鹏程数”，例如:80000、11125都是五位数的“鹏程数”。

特别地，我们把各个数字均不为零的“鹏程数”叫作“真鹏程数”。

(1)求出所有三位“鹏程数”之和

(2)求出四位“真鹏程数”的四个数字

含有2个0的数，即100、200、……、900，共9个，和为4500；

含有1个0的数，即a0b或ab0，需要满足ab=a+b，即（a-1）（b-1）=1，只能是a=b=2。含有1个0的鹏程数即为202或220，和为422；

真鹏程数，abc=a+b+c，设a≥b≥c，且c等于1，即ab=a+b+1，由公式可知(a-1)(b-1)=ab-a-b+1=2，可知a、b为3和2。当c等于2或更大数时，无解，即真鹏程数有321、312、231、213、132、123这6个，和为1332。

综上，所有三位“鹏程数”的和为4500+422+1332=6254。

(2)设四位“真鹏程数”的四个数字分别为a、b、c、d，且a≥b≥c≥d，可知如d≥2或d等于1，c大于等于2时均无解，可求得c=d=1，代入得ab=a+b+2，a=4，b=2。四位“真鹏程数”的四个数字分别为4、2、1、1。

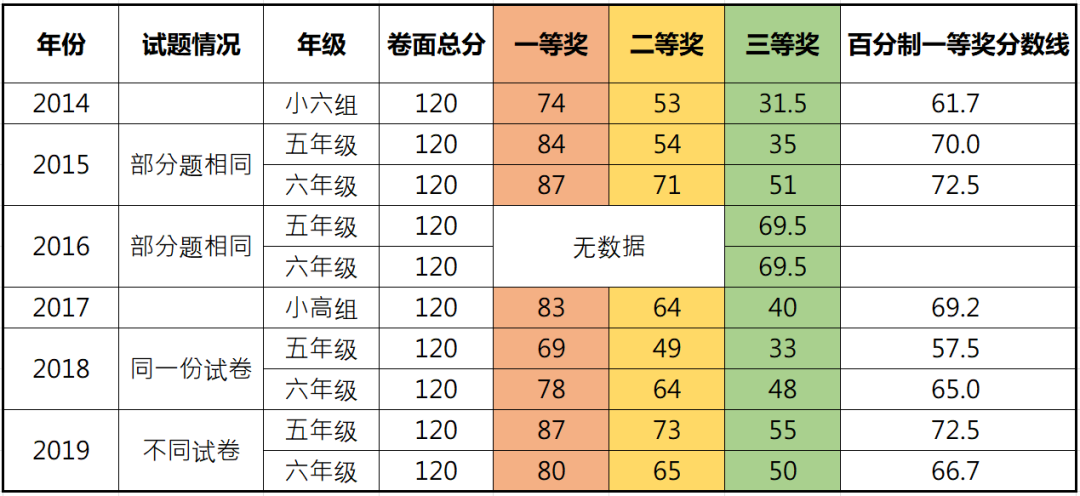
2019年六年级一、二、三等奖分数为80分、65分、50分。