“数学花园探秘”(ACM)全面深度剖析
试卷结构及知识点
1、题目组成、知识点分析
ACM比赛的题目构成:
一档题:4道,每道8分,共32分
涉及知识点:计算,几何计数,应用题,数字谜;
二档题:4道,每道10分,共40分
涉及知识点:组合(计数、逻辑推理),数论(整除,因数倍数);
三档题:3道,每道题12分,共36分
涉及知识点:数论、几何、行程,或逻辑推理与其他模块结合;
2、试卷难度
难度值
迎春杯模拟赛难度值大概为0.3(平均分÷总分=难度值),本次模考平均分40,正好是0.3。
所以说,这次的分数基本能够代表如果你“今天”去考迎春杯所能拿到的分数!
3、四大考点的重点难点剖析+学习思路
这个部分将从“知识点模块”、“每题得分率”、“每题平均用时”、“标准错误答案”等几项数据,简要分析迎春杯的考试重点、难点,给出复习思路,分享一些解题技巧。
本次考试的每题得分率
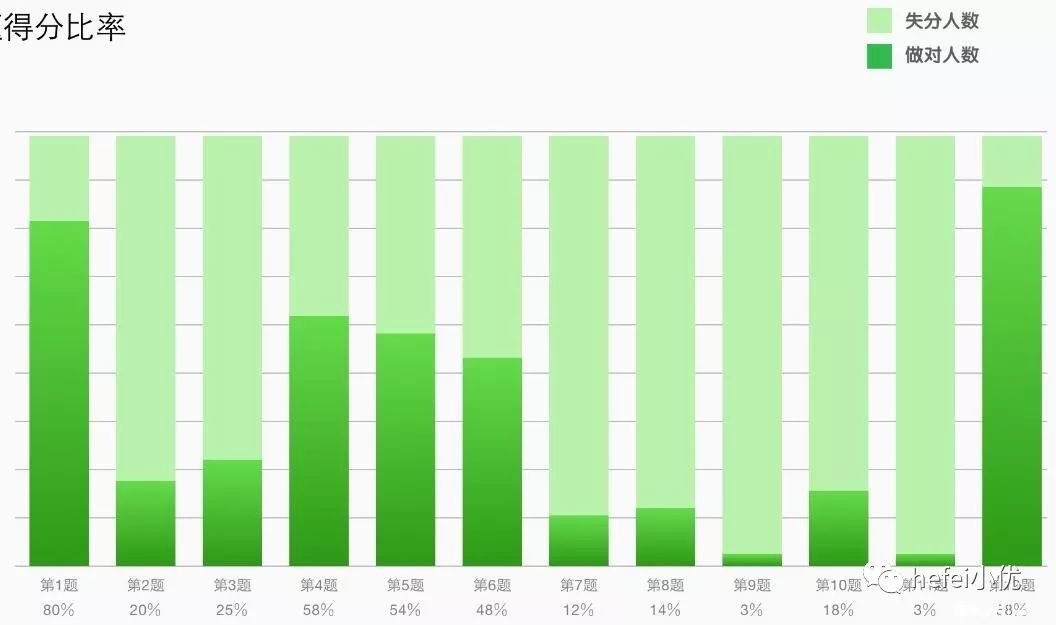
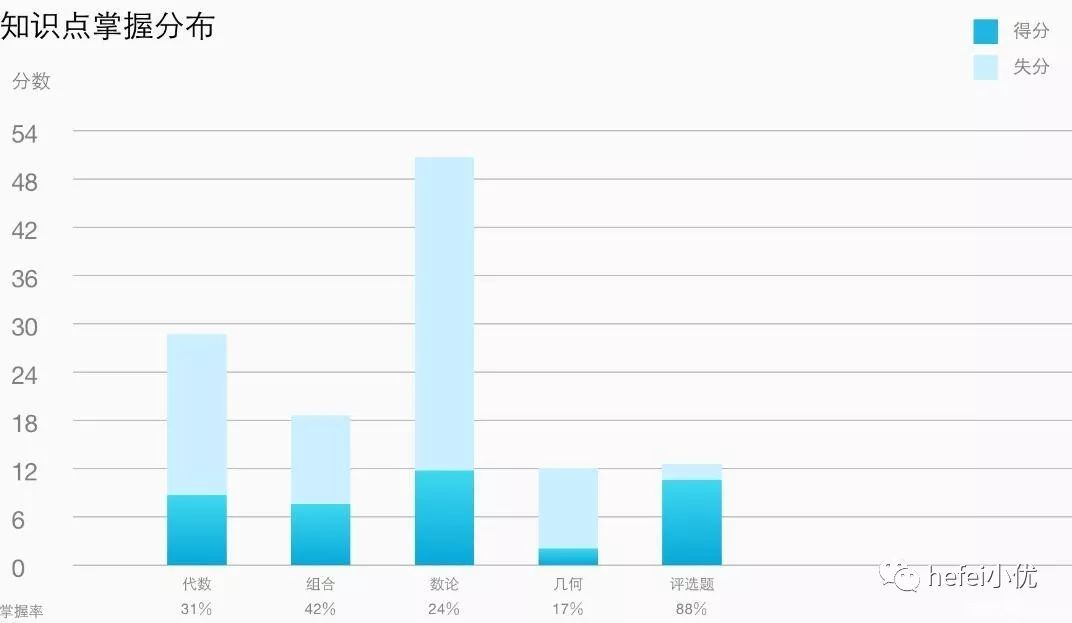
按知识点划分的得分率
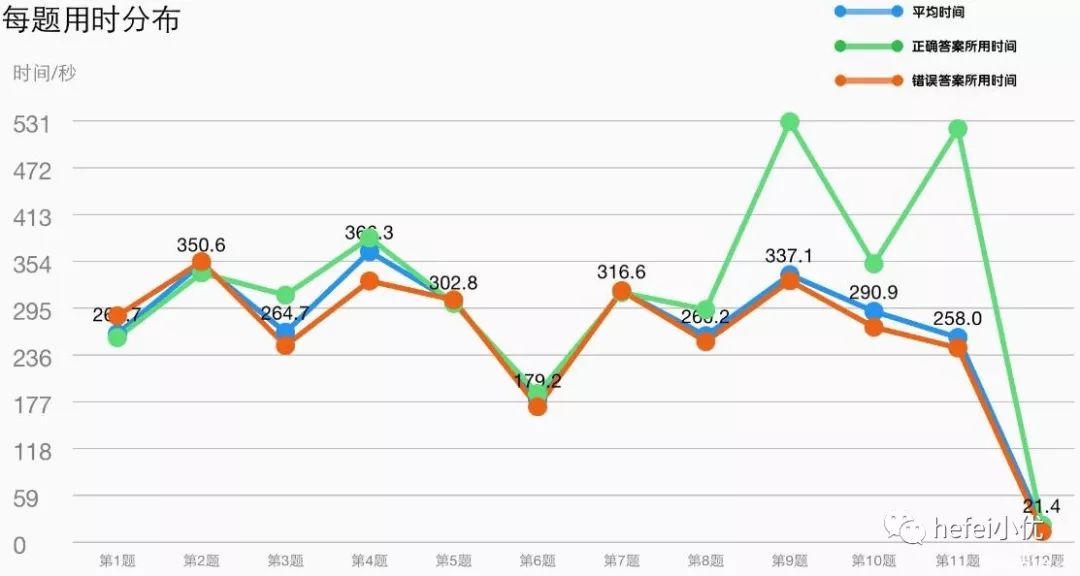
每题平均用时
(全体平均用时、正确答案平均用时、错误答案平均用时)
一档“送分”题
(计算、数字谜、几何计数、简单几何、应用题)
1)下面算式的计算结果
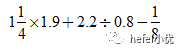
知识点 | 分数计算 | 难度 | ★ |
正确答案 | 5 | 得分率 | 80% |
典型错误答案 | 5.25 | 全体平均用时 | 260秒 |
优才支招:
1、迎春杯第一题必考分数计算,题目特点为:可猛算,可巧算
2、得分率让人大跌眼镜,这道题如果做错了,建议找一些习题集,集中做练习,如果能每天练习就更好了,习题集的选择随意,反正都是计算。
3、典型错误答案中,有人答小数,有人答分数。在迎春杯的所有题目中,答案均为整数,如果你得出的是小数,一定就是做错了!
2)右图中,共有__________个三角形
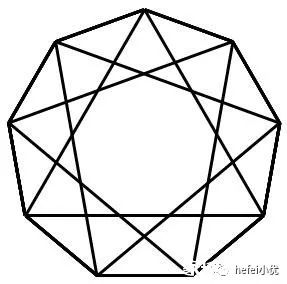
知识点 | 几何计数 | 难度 | ★★ |
正确答案 | 57 | 得分率 | 20% |
典型错误答案 | 54、48 | 全体平均用时 | 350秒 |
优才支招:
1、一档题中,“几何计数”或“简单几何计算”会二选其一,而几何计数从来都是“送不出分的送分题”,作为必考内容必须搞定它!
2、解题技巧:1)按块数分类之后,有序枚举 2)利用对称图形的特点解题。
3)6个同学约好周六上午8:00—11:30去体育馆打乒乓球,他们租了两个球桌进行单打比赛,每段时间都有4个人打球,另外两人当裁判,如此轮换到最后,发现每人都打了相同的时间,请问:每人打__________分钟。
知识点 | 应用题 | 难度 | ★★ |
正确答案 | 140 | 得分率 | 25% |
典型错误答案 | 35、70 | 全体平均用时 | 260秒 |
优才支招:
1、迎春杯的一档题应用题很有特点,绝不会考“和差倍、年龄问题、牛吃草”之类的典型应用题,而是突出“创新”,用新的情景、新的背景让孩子们利用平时所学的知识解决问题,对孩子的阅读能力要求很高;另一种考法是应用题与数论相结合。
2、这道题目的阅读难度并不高,但很多孩子不能理解题意,所以这题得分率低也是情理之内的事情。
3、复习建议:做学而思白皮中的应用题,尤其是找题干长的做(注意,学而思白皮其他的模块别做)。
4)右图乘法算式中,两个乘数的和是_______
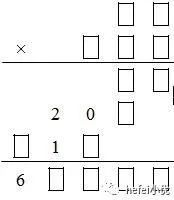
知识点 | 数论(数字谜) | 难度 | ★★ |
正确答案 | 999 | 得分率 | 58% |
典型错误答案 | 63308、998 | 全体平均用时 | 360秒 |
优才支招:
1、一档题中,数字谜必考,以竖式数字谜为主,这道题就是典型题型,题干中大概率出现年份相关的条件,但答案不会是年份,蒙也别蒙年份!
2、知识点:首尾分析大小范围、末尾分析个位数字,重复位也是突破口,进位分析会涉及。
二档核心题
(数论和组合的天下)
5)一个五位数,各位数字互不相同,并且这个五位数能同时被20、16、11、18都整除,那么这样的五位数中,最小的是__________.
知识点 | 数论(整除) | 难度 | ★★ |
正确答案 | 15840 | 得分率 | 54% |
典型错误答案 | 7920、63360 | 全体平均用时 | 302秒 |
优才支招:
1、二档题数论一般会有两道,知识点为整除、因倍。
2、这道题难度有些低,迎春杯数论不会这么简单。
3、典型错误答案中,7920体现了孩子的审题问题,一看会做就开始嗨……而63360就是不会求多个数的最小公倍数。
6)甲、乙、丙、丁4个人聚在一起,甲说:“我们之中至少有1个人说的是对的”;乙说:“我们之中至少有2人说的是对的”;丙说:“我们之中至少有1个人说的是错的”;丁说:“我们之中至少有2个人说的是错的”.
那么,这4个人中,说对的人有人.
知识点 | 组合(逻辑推理) | 难度 | ★★ |
正确答案 | 3 | 得分率 | 48% |
典型错误答案 | 2 | 全体平均用时 | 179秒 |
优才支招:1、二档题组合,如果出现逻辑推理,有两个出题方向:1)类似这道题的纯逻辑推理,利用假设法解决,难度较低;2)与其他模块结合,一般为应用题,稍有难度。
2、除此之外,还有可能考到“体育比赛”、“数独”、“简单的操作类题目”,这些题目可替换逻辑推理。
7)将1、2、3、4、5、6、7填入右图的小六边形中,要求每个数和相邻的数都是互质的,那么满足要求的填法共有__________种.

知识点 | 组合(计数) | 难度 | ★★★ |
正确答案 | 72 | 得分率 | 12% |
典型错误答案 | 36、12 | 全体平均用时 | 316秒 |
优才支招:
1、二档组合题,必有一道计数,绝不会考单纯的“插空法、插板法、捆绑法”之类的技巧,做题的时候千万别想偏了,应该对题目中的“特殊元素”进行分类枚举,然后才是排列。迎春杯计数题目的重点是枚举法,不是排列组合!
2、这道题出的非常漂亮,放在模考着实有些“浪费了”,做错了的孩子,一定要把这道题吃透,不光是能“听明白”解析,而是要求能吃透其中的道理!
8)我们把用1、2、7、8各一个组成的24个不同四位数称作如意数,神奇在于其中五个不同的如意数的和也是如意数,那么这五个如意数的和是_______
知识点 | 数论+组合 | 难度 | ★★★★★ |
正确答案 | 8712 | 得分率 | 14% |
典型错误答案 | 8721 | 全体平均用时 | 266秒 |
优才支招:
1、这是二档题的第二道数论,正常应该考察因倍的相关知识,而这道题是一道数字谜,用上了弃九法的进位分析和枚举,过程分析之复杂,绝对超越了第8题应有的难度。
2、全体平均用时是266秒,而回答正确的平均用时是295秒,这说明孩子做数字谜,还是靠感觉多于靠分析,这反而省下了很多时间。给大家的建议是:如果遇到这种题目,简单分析之后发现情况太多,就选择性放弃,先看后面的题,已经到第八题了,别在那死磕!
三档欣赏题
(数论、几何、行程,还有可能是组合结合这三个模块的逻辑推理)
9)大圣和小龙的钱包里都只有1元、10元、100元的纸币,而且两人的每种纸币都不到10张。两人惊奇的发现,大圣钱包里的钱数是小龙的两倍,但张数只有小龙的一半,那么大圣钱包里最多有__________元钱。
知识点 | 数论 | 难度 | ★★★★ |
正确答案 | 510 | 得分率 | 3% |
典型错误答案 | 300 | 全体平均用时 | 337秒 |
优才支招:
1、欣赏题的数论就没法给大家说知识点了,什么知识都有可能出到这一档中,这道题用到了弃九法的知识点,很多孩子都没有学过,或者不太了解,做对的也基本用的枚举法。
2、弃九法非常重要,在有关数字和的数论题目中,都是关键的分析步骤,一定要会。
3、这道题“包装”的非常精巧,把一道有关弃九法的数论题目包装成了一个现实生活中的情景,非常精彩!
4、典型错误答案中的300,其实是个很靠谱的答案,只不过由于题目稍有些绕,做着做着就把条件想成“大圣的钱数和张数都是小龙的一半”了。
10)右图中,大六边形的面积为2016,A、B、C、D、E、F分别为各边中点,那么,阴影部分的面积是__________.
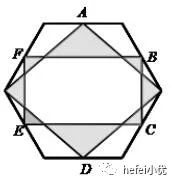
知识点 | 几何 | 难度 | ★★★★ |
正确答案 | 504 | 得分率 | 18% |
典型错误答案 | 672 | 全体平均用时 | 290秒 |
优才支招:
1、一道标准的迎春杯几何题目,具备“对称”、“美观”的特点,可以用很多方法解决,核心都是:割补、对称、旋转等。
2、强调一点:迎春杯几何题,只要是对称图形,都可以用分割的方法来做;至于所谓的五大模型,什么鸟头、燕尾的都不考,当然你非用那些方法解答也是可以的,但并不是什么题都适用,而格点图是无敌的!
3、这题放模考也是浪费了,哎,又一个图形被出过了,已经没几个图可出了……
11)甲、乙两人同时开车从A地出发,在AB之间往返.甲调头后,在距离。B地2千米的C点与乙相遇,相遇后,甲的速度降低了1/6,乙保持原速,调头后,在经过C点后,速度提升了1/4,结果在距离A地5千米的地方追上甲。那么,AB两地相距__________千米.
知识点 | 行程 | 难度 | ★★★★ |
正确答案 | 25 | 得分率 | 3% |
典型错误答案 | 12、2016 | 全体平均用时 | 258秒 |
优才支招:
1、行程问题考点:多人多次,走走停停(结合数论),变速问题等,还有一个最关键的,在题目中一般会用到比例行程的知识!
2、行程是个老大难问题,出再简单的行程得分率也不会超过20%,除非你是有“行程特长”不然不建议在初赛阶段在行程上花太大功夫。
3、这道题也出的很漂亮,除了常规的比例行程方程方法,还可以用很巧妙的算数方法解决。




全部 0条评论