2015年小高组决赛A卷

2. 一张边长为10厘米的正方形纸片，如图对折两次，再沿两边的中点连线剪掉一个角之后，那么把余下部分展开为单层纸片的面积是__________平方厘米．

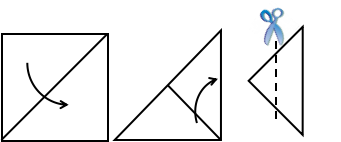
〖答案〗75

8. 右图的图案由1个圆和2个大小相同的正方形组成（2个正方形的公共部分为正八边形）．如果圆的半径为60厘米，那么阴影部分的面积是_________平方厘米．（π取3.14）

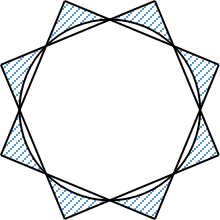
〖答案〗3096

2016年小高组决赛A卷

8. 如图，正十二边形的面积是2016平方厘米，那么图中阴影部分的面积是          平方厘米．

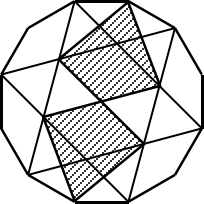
〖答案〗672

11. 如图，直角三角形ABC中，AB的长度是12厘米，AC的长度是24厘米，D、E分别在AC、BC上．那么等腰直角三角形BDE的面积是__________平方厘米．

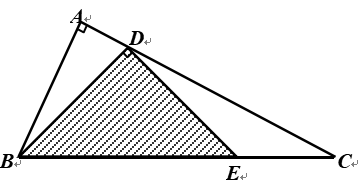
〖答案〗80

2017年小高组决赛A卷

2. 一个边长为100厘米的正五边形和五个扇形拼成如图的“海螺”，那么这个图形的周长是________厘米（π取3.14）．

〖答案〗2384

10. 如图，P为四边形ABCD内部的点，AB:BC:DA=3:1:2，∠DAB=∠CBA=60°．图中所有三角形的面积都是整数．如果三角形PAD和三角形PBC的面积分别为20和17，那么四边形ABCD的面积最大是________．

〖答案〗147

2018年小高组决赛A卷

2. 老师在黑板上画了两个相同大小的等腰直角三角形；小红在一个三角形内画了一个最大的四分之一圆，小权在另一个三角形内画了一个最大的半圆（如图所示）．已知小红画出的四分之一圆面积为60，那么小权画出的半圆面积为________．（Π取3.14）

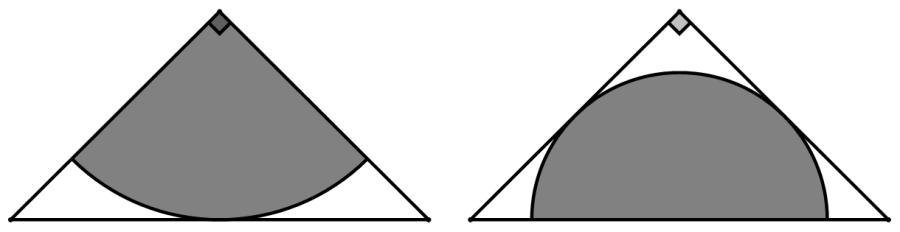
〖答案〗60

13. 如图，菱形ABCD的边长是18．如果三角形CDE是等腰直角三角形，求四边形ABEF的面积．

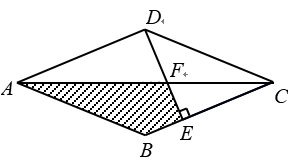
〖答案〗81

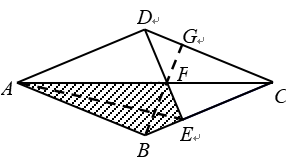
〖解析〗如图，根据对称性，BG和DE关于AC对称，△DGF和△BEF关于AC对称．

因为△DGF是等腰直角三角形，所以△BEF也是等腰直角三角形，从而BE=EF．

（1）因为AD和EC平行，所以S_△AEF=S_△DFC．

（2）比较△ABE与△EFC，分别以BE和EF为底，那么它们的底相等，高也相等．所以S_△ABE=S_△EFC．由（1）（2），

S_ABEF=S_△DEC=DC²÷4=18×18÷4=81．

2019年小高组决赛A卷

3.右图中的正八边形边长为200，以正八边形八个顶点为圆心裁掉8个半径为100的扇形，那么剩余部分（图中阴影所示）的周长是________．（圆周率取3.14）

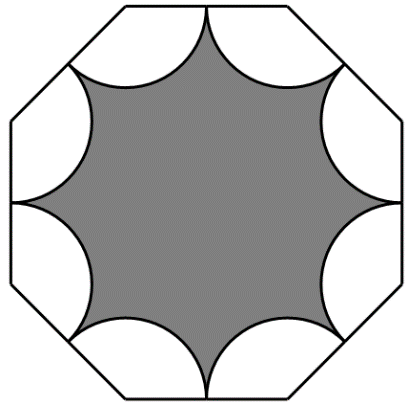
〖答案〗1884

10.如图，四边形ABCD中，∠ABC=90°，∠BAC=30°，∠CDA=120°，且AD=BC+CD，三角形ABC面积为30，则三角形CDA的面积为___________．

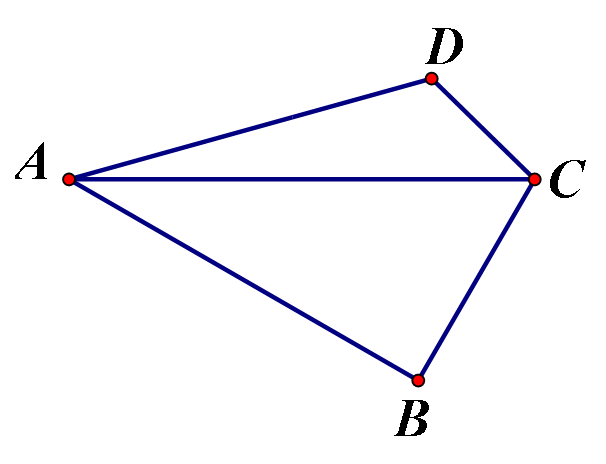
〖答案〗15

点评：几何一直都是所有数学比赛的必考题型，数学花园探秘近些年小高决赛一般都是放两道几何题，一道题在一档，以圆与扇形的计算为主的简单题，另外一道在二档后面或三档前面的位置，以考察正多边形和五大模型为主的难题。

对于前面的简单题同学们需要注意两点，一是计算方法是否简便，二是运算结果是否正确，做好这两点，前面的这道8分题就到手了。对于后面的难题，首先需要同学们记住一些结论和常见辅助线的构造方法，其次就是看各位同学平时的做题功底了。如果实在实在没办法，试一试“度量找关系”大法，没准有一些奇效。综上，对于几何部分，前面的一题是必保的，后面的要尽量争取。