一、选择题

1、中国共产党成立于（）年

A. 1919年             B. 1921年             

C. 1927年             D. 1949年

【答案】B

【解析】好像这部分题都不用解析，都是孩子们应该知道的.1921年7月1日是共产党成立纪念日，2021年7月1日在天安门召开了隆重的建党100周年庆典，仿佛还在今年……

2、中国共产党党徽为（）和锤头组成的图案，是中国共产党的象征和标志

A. 镰刀                B. 锤头                

C. 斧头                D. 齿轮

【答案】A

【解析】中国共产党党徽为镰刀和锤头组成的图案，图案为金黄色.锤子、镰刀代表工人和农民的劳动工具，象征着中国共产党是中国工人阶级的先锋队，代表着工人阶级和广大人民群众的根本利益.黄色象征光明.

3、中国少年先锋队队旗是（）加火炬的红旗.队旗中央的五角星，代表中国共产党的领导，火炬象征光明，红旗象征革命胜利.

A. 三角形             B. 四角形             

C. 五角星             D. 六芒星

【答案】C

【解析】题目里写了五角星...这题答错还挺难的

4、中国少年先锋队队歌《我们是社会主义接班人》的发源地是（）

A. 井冈山             B. 瑞金                 

C. 延安                D. 厦门

【答案】D

【解析】原为电影《英雄小八路》的主题歌.电影记载了金门炮战时期，厦门禾山区第四小学学生成立“前线少年支前活动大队”支援解放军的故事.后学生被评为“英雄小八路”，根据真实事迹改编的同名电影也于1960年在厦门拍摄，主题歌定为周郁辉作词、寄明作曲的《我们是共产主义接班人》.1978年该歌曲被定为中国少年先锋队队歌.

5、1949年10月1日，（）在北京天安门城楼升起五星红旗，向全世界宣布中华人民共和国成立了.新中国的成立解决了国家统一和民族独立这两个关系中华民族伟大复兴的关键性问题.

A. 毛泽东             B. 周恩来             

C. 刘少奇             D. 朱德

【答案】A

【解析】常识吧，不解释了...就是凑齐了第4套人民币100元的四大领袖组合~小朋友们估计都没见过这张人民币了

6、1964年10月，中国第一颗（）爆炸成功.

A. 导弹                B. 原子弹             

C. 氢弹                D. 中子弹

【答案】B

【解析】我国第一枚导弹“1059”导弹（后称为东风一号）于1960年11月5日发射成功.

我国第一枚原子弹于1964年10月16日爆炸成功.我国第一枚氢弹于1967年6月17日空爆成功.我国第一枚中子弹于1984年12月19日实验成功.

7、被誉为“杂交水稻研究的开创者”的中国工程院院士是（）

A. 童第周             B. 李振声             

C. 袁隆平             D. 赵振东

【答案】C

【解析】童第周（1902-1979）是我国著名的生物学家，中国海洋科学研究奠基人，中国实验胚胎学主要创始人，被誉为中国克隆之父.小学语文课文有一篇写的就是童第周研究金鱼尾巴的，印象很深.李振声（1931-）是我国著名的遗传学家，中国小麦远缘杂交之父.前不久刚刚去世的袁隆平（1930-2021）是我国著名的农业科学家，杂交水稻之父.袁李二人研究方向一稻一麦，有“南袁北李”之称.赵振东（1966-2020）是我国著名的病原生物学和免疫学家.

8、1997年7月1日，（）回归祖国.

A. 香港                B. 澳门                 

C. 台湾                D. 黑瞎子岛

【答案】A

【解析】香港于1842年割让于英国殖民统治，1997年7月1日回归，成为我国特别行政区.澳门于1887年割让于葡萄牙殖民统治，1999年12月20日回归，成为我国特别行政区.中国历代政府对台湾实行管辖权.2004年中俄划定位于黑龙江、乌苏里江交汇处的黑瞎子岛主权范围，约定西半部归中华人民共和国管理，东半部为俄罗斯联邦管理，解决了几十年以来的领土争议.

9、2009年被评为“100位新中国成立以来感动中国人物”的“人民数学家”是（）.

A. 苏步青             B. 华罗庚            

 C. 陈建功             D. 吴文俊

【答案】B

【解析】这几位都是数学家、中科院院士

录100位新中国成立以来感动中国人物：

丁晓兵、马万水、马永顺、马恒昌、马海德、中国女排五连冠群体、孔祥瑞、孔繁森、文花枝、方永刚、方红霄、毛岸英、王杰、王选、王瑛、王乐义、王有德、王启民、王进喜、王顺友、邓平寿、邓建军、邓稼先、丛飞、包起帆、史光柱、史来贺、叶欣、甘远志、申纪兰、白芳礼、任长霞、刘文学、刘英俊、华罗庚、向秀丽、廷·巴特尔、许振超、达吾提·阿西木、邢燕子、吴大观、吴仁宝、吴天祥、吴金印、吴登云、宋鱼水、张华、张云泉、张秉贵、张海迪、时传祥、李四光、李春燕、李桂林和陆建芬夫妇、李素芝、李梦桃、李登海、杨利伟、杨怀远、杨根思、苏宁、谷文昌、邰丽华、邱少云、邱光华、邱娥国、陈景润、麦贤得、孟泰、孟二冬、林浩、林巧稚、林秀贞、欧阳海、罗映珍、罗健夫、罗盛教、草原英雄小姐妹、赵梦桃、钟南山、唐山十三农民、容国团、徐虎、秦文贵、袁隆平、钱学森、常香玉、黄继光、彭加木、焦裕禄、蒋筑英、谢延信、韩素云、窦铁成、赖宁、雷锋、谭彦、谭千秋、谭竹青、樊锦诗.

10、2022年冬季奥林匹克运动会主办城市是（），该城市成为第一个举办过夏季奥林匹克运动会和冬季奥林匹克运动会以及亚洲运动会三项国际赛事的城市.

A. 上海                B. 东京                 

C. 北京                D. 西安

【答案】C

【解析】北京于1990年承办第11届亚运会、2008年承办第29届夏季奥运会、2022年承办第24届冬季奥运会.上海和西安未曾承办.

广州和杭州分别与2010年和2022年承办亚运会.上海和西安未曾承办.

东京于1958年承办亚运会，1940年承办夏季奥运会（取消），1964年承办夏季奥运会，2020年承办夏季奥运会（延期至2021年举办）

二、填空题

1、2020年中国政府在第七十五届联合国大会上提出，中国力争于2030年前二氧化碳排放达到峰值不再增长，达到峰值之后再慢慢减下去；争取2060年前实现碳中和，就是通过植树和节能减排等方式，将排放二氧化碳全部抵消掉.关于碳排放有以下数据：

一辆汽车每行驶2万千米，排放二氧化碳2吨.飞机每运输1吨物品飞行1万干米，排放二氧化碳3.2吨.一个人每天呼吸释放二氧化碳1140克.一棵中等大小的植物每年吸收二氧化碳6干克.一台电脑每年排放二氧化碳10.5千克.一个电暖器每年排放二氧化碳600千克.一台洗衣机每年间接排放二氧化碳7.75千克.一台冰箱每年间接排放二氧化碳6.3千克.

假设某中等城市里的一个六口之家，每年购买国外商品：水果50千克、鱼肉乳品100千克、饮料酒水50千克（为方便计算，国外商品均空运，距离均以1万千米计）；2台汽车每年用于城市交通和旅游每台行驶1万千米；使用家用电器有1台电脑、4个电暖气、1台洗衣机、1台电冰箱.请回答要达到碳中和，这家人每年（365天）平均每人要至少种（）棵中等大小的植物，若这些中等大小的植物每棵需要4平方米土地生存，这个家庭每年至少需要（）平方米土地（结果取整数）

【答案】211,5041

【解析】想起来一句至理名言——胆大心细脸皮厚.胆大——不能被题目字数吓怕；心细——不要出错，尤其换算单位；脸皮厚——这么难受的题就别花时间检查了，有检查的工夫又做两道了——当然除非其他题做完了，这道题还是需要检查的，毕竟这题难度并不大

以下拿好计算器，并分步书写

全家全年碳排量包含①6人呼吸②飞机空运③汽车④电器

①6人×1140克×365天：6×1.14×365=2496.6（kg）

②200千克货物×3.2吨二氧化碳/吨货物：0.2×3200=640（kg）

③2台×1万千米×2吨二氧化碳/2万千米：2000（kg）

④10.5+600×4+7.75+6.3=2424.55（kg）

2496.6+6400+2000+2424.55=7561.15（kg）

每人植树：7561.15÷（6×6）≈210.04，向上取整为211棵

需要种树：7561.15÷6≈1260.21，向上取整为1261棵（感谢小杰老师等订正）

土地面积：1261×4=5044平方米

2、一个三角形，三条边长分别为整数a,b,c，并且ab+bc+ca=133，则这个三角形的周长为（）

【答案】20

【解析】我当年的师傅小胖老师说，看到题目涉及“因倍、互质、整除、乘积”的时候就要考虑能不能用分解因数的办法解决

ab+bc+ac=133

a(b+c)+bc=133

让bc也出现一个(b+c)的因数，需要把bc变为b(b+c)-b²

a(b+c)+b(b+c)-b²=133

(a+b)(b+c)=133+b²

考虑b不会太大（b若太大，而ac太小，则无法凑成三角形，ac之一太大，则ab+bc会超过133），大约在10以内，所以可以针对b进行枚举

①b=1,133+1=134=2×67

②b=2,133+4=137是质数

③b=3,133+9=142=2×71

④b=4,133+16=149是质数

⑤b=5,133+25=158=2×79

⑥b=6,133+36=169=13²，即a+b=b+c=13，即a=c=7，周长为6+7+7=20

考场上算到这里就可以了，但此处解析继续枚举结束

⑦b=7,133+49=182=2×7×13，即a+b=14，b+c=13，周长同⑥

⑧b=8,133+64=197是质数

⑨b=9,133+81=214=2×107

⑩b=10,133+100=233是质数

⑪b=11,133+121=254=2×127

⑫b=12,133+144=277是质数

当b≥12时，a+c≥13，ab+bc≥156即不再有解

3、对于自然数n，定义“阶乘”运算：n!=1×2×3×…×n，如5!=1×2×3×4×5=120.已知自然数a≥b≥c≥d≥1，且a!×b!×c!×d!=3!×16!，则a+b+c+d的最大值为（）

【答案】24

【解析】还有一句至理名言，叫“积一定差小和小”这题其实并不是abcd积一定，所以并不能直接推断出abcd越接近和越小。但可以通过这方面的印象进行思考方向上的引导

刚才那句“遇到xxx就分解因数”，咱们分解一下3!×16!

3!×16!=2¹⁶×3⁷×5³×7²×11×13

abcd中需要包含1个13，故a≥13，且a＜17

abcd中需要包含1个11，而a!包含11，则b≤10

①a=13，13!=2¹⁰×3⁵×5²×7×11×13，则b!×c!×d!=2⁶×3²×5×7，若b=7，则b!=2⁴×3²×5×7，c×d=2²，c=d=2，a+b+c+d=24，若b=8，8!=2⁷×3²×5×7＞2⁶×3²×5×7无解；

②a=14，14!=2¹¹×3⁵×5²×7²×11×13，则b!×c!×d!=2⁵×3²×5，若b=5，则b!=2³×3×5，c×d=2²×3，c=3，d=2，a+b+c+d=24；若b=6，则b!=2⁴×3²×5，c=2，d=1，a+b+c+d=23；

③a=15，14!=2¹¹×3⁶×5³×7²×11×13，则b!×c!×d!=2⁵×3，b=4，c=d=2，a+b+c+d=23;

④a=16，14!=2¹⁵×3⁶×5³×7²×11×13，则b!×c!×d!=2¹×3，b=3，c=d=1，a+b+c+d=21;

以上答案中，a+b+c+d最大为24

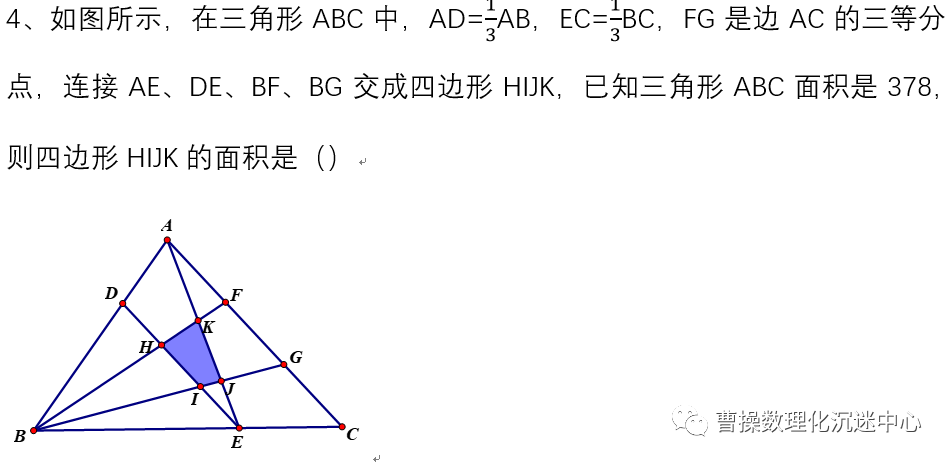
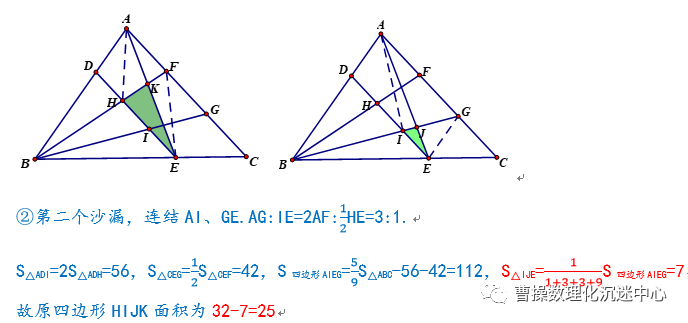
2、运动会上8支球队进行单循环比赛，求最大的正整数k，使得在任意进行k场比赛后，总能找到三支球队，使得这三支球队还未进行比赛.

【答案】11

【解析】这题的解析我写得有点啰嗦，其实是我自己做题的思考过程，解析应该更精炼一些，但我还是想把我的所有思考都放上来.感兴趣的同学肯定能看出来我的思路~

8支球队进行单循环，总共应进行28场比赛.如果已经进行k场，则还有(28-k)场没有进行.

在平面上画出任意三点不共线的8个点A、B、……、H代表8支队伍，将两个点连结实线段，代表两队已经比赛，而将两个点连结虚线段，代表两队还未比赛.

问题变为：构造一个情况，存在k条实线段，使得由上述28条线段中首尾相连的3条构成的三角形中，存在三条边都是虚线段的——虚线三角形，求k的最大值.

问题可以进一步变为：在本模型中存在m条虚线段，求m的最小值，使得虚线三角形一定会出现

包含某一条确定实线段的三角形共有6个（比如以AB为边的三角形共有ABC、ABD、……、ABH共6个），平面共存在C(8,3)=56个三角形，满足28×6÷3=56（以某线段为边的三角形共6个，28条边有6×28个，但每个三角形都被算了三次——三条边各算一次——故实际共有6×28÷3=56个）.避免出现虚线三角形，则允许56个三角形各有2条边是虚线，但每个虚线都在6个三角形中，故虚线最多添加56×2÷6=18.条.

尝试证明18条虚线一定出现虚线三角形——18条虚线会出现36个“虚端点”，将其平均分布在8个顶点，36÷8=4……4，根据抽屉原理，肯定有一个点连了5条虚线，假设为AB、AC、AD、AE、AF，而B、C、D、E、F五点之间不能再连虚线（否则直接出现虚线三角形），则至少有C(5,2)=10条实线，而此时剩余线段均为虚线，存在虚线三角形ABG等.

其实在构造的过程中发现，17条虚线出现34个“虚端点”时就存在34÷8=4……2，根据抽屉原理，AB、AC、AD、AE、AF为虚线，B、C、D、E、F五点之间为实线，在剩下的线中只存在1条实线（假设最后一条实线连结H），则G出发的线段皆为虚线，存在虚线三角形ABG等.

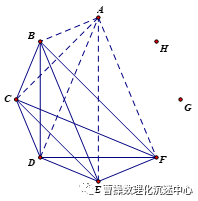
构造16条虚线不出现虚线三角形的情况：第一组四个点ABCD之间互相以实线连结，第二组EFGH之间互相以实线连结，而第一组和第二组连线为虚线.如图

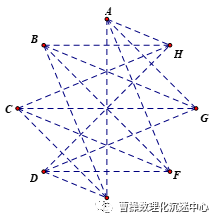
故k=12无法保证出现虚线三角形，k=11为最大值.

四、编程填空

1、将任意一个大于1的正整数n输入到程序中，程序将按照以下步骤执行：

步骤1：输出n的值，如果n等于1，结束整个程序；否则执行步骤2；

步骤2：令p的值等于n除以2的余数，执行步骤3；

步骤3：当p等于0时，将n的值除以2，跳转至步骤1；否则，将n的值乘以3再加上1，跳转至步骤1；

现在将正整数27输入到程序中，程序会输出若干个数，则数字161是程序输出的第（）个数

【答案】14

【解析】分析成下图流程图：中间实际是一个判断奇偶的过程

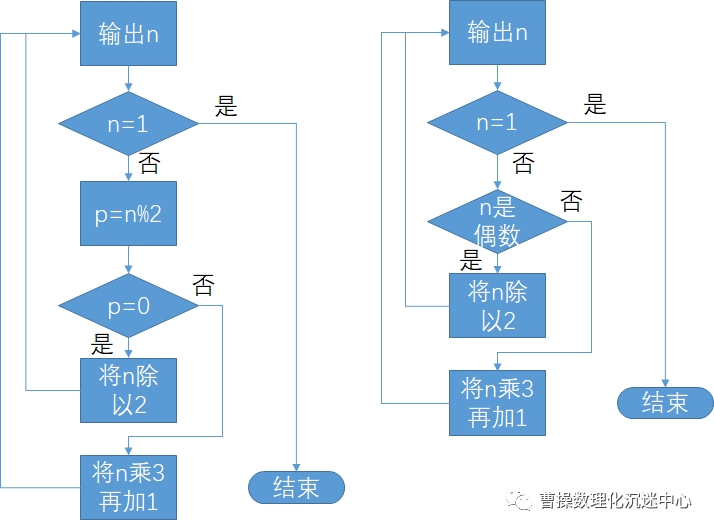
您从“乘以”这俩字也能看出本题的包浆了.

输入n=27时，第一次输出82，第二次输出41，第三次输出124，第四次输出62，第五次输出31，第六次输出94，第七次输出47，第八次输出142，第九次输出71，第十次输出214，第十一次107，第十二次322，第十三次161.慢慢算，别计算出错，不难.