试题1：有一些整数排成一列，其中第一个数是100，前两个数的平均数比100小1，前三个数的平均数比前两个数的平均数小1，前4个数的平均数比前三个数的平均数少1，前五个数的平均数比前四个数的平均数少1，……，等等。问第40个数的是多少？

武汉童老师分析：

第一个数：100；

第二个数：因为前2个数平均数100-1=99，所以前2个数和为99×2=198，第二个数是：198-100=98 ；

第三个数：因为前3个数平均数99-1=98，所以前3个数和为98×3=294，所以第3个数为：294-100-98=96；

方法1：第一个数100=2×50，第二个数96=2×49，第三个数96=2×48，所以第40个数：2×（50-10+1）=22，2的50倍到2的1倍共50个数，除了前面40倍，后面还有50-40=10，所以第40个数为倒数第10+1=11个；

方法2：前1个苹果数100，前2个平均数99，前3个平均数为98，因为1+100=101，2+99=101，3+98=101，所以前N个平均数为101-N，所以前39个数的平均数为：101-39=62，前40个数的平均数为：101-40=61，所以前39个数总和=39×62=2418，前40个数的总和=40×61=2440，所以第40个数为：2440-2418=22 。

点评：此题主要考察平均数知识，考察找规律能力。难度一般。

试题2：有若干份千克力，每一份巧克力的数目要么是4颗，要么是9颗，4颗一份的巧克力和9颗一份的巧克力都有足够多份。小恒现在从这些巧克力中取出不超过99颗，只能整份整份的取，取的总份数不受到限制。那么小于100的整数里面，有多少种数目是小恒取不到的？（例如1颗巧克力是取不到的。）

武汉童老师奥数分析：

通过枚举，在颗数1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21、22、23中，其中的1、2、3、5、6、7、10、11、14、15、19、23这12种颗数无法取到。

同时24、25、26、27都可以取到，所以接下来：24、25、26、27四种不断分别加上4颗，就可以得到28到99颗的所有情况。

所以只有12种没有办法取到。

点评：对于三四年级中年级学生来说，通过枚举，通过后边的取数（每次加4）的规律构造，是学有余力学生可以理解和做到的。

试题3：某个传染病医院有病床500张，医生20人。因疫情需要，再增加500张病床。若一个医生最多可以管理20张病床，且每个医生7天之中必须休息1天，那么这个医院还需要增加多少名医生？

武汉童老师奥数分析：

方法1：工作休息时间周期是7天一个周期；工作是6天一个周期，所以我们可以取一个时间为7也为6的倍数即最小为6×7=42天为一个大周期。

500+500=1000张

1000张床1天需要多少医生？

1000÷20=50人

把1个医生1天工作看作1份，那么每天医生工作1×50=50份。

42天共需要：42×50=2100份工作。

每个医生42天只做了几份工作？

42÷7×6=36天即1×36=36份

所以医生需要：

2100÷36=58……2，所以至少需要58+1=59个。

还需要增加：59-20=39个。

方法2：

500+500=1000张

1000÷20=50人

一个医生一天工作为1份

50人医生7天工作：50×7=350份

1个医生7天只做：1×（7-1）=6份

医生总数：350÷6=58人……2份

至少需要58+1=59人

再增加：59-20=39人。

点评：借助了1份来转化和理解。

试题4：有一个农民养了100只鸡，从今年3月1日起它们开始下蛋。第一天只有一只母鸡下了1个蛋，第二天开始又有一只母鸡下了蛋，以后每天都多了1只母鸡下蛋，直到第100天所有母鸡都下了蛋。而且每只母鸡开始下蛋后每天都会下一个蛋。农民打算从某一天开始，每天出售这些母鸡下的蛋100个。问最早可以从哪天开始出售鸡蛋？

武汉童老师奥数分析：

方法1：

鸡蛋总数：1+2+3+4+5+……+99+100=5050个

每天卖100个，可以最多卖几天？

5050÷100=50天……50个

最多可以卖50天。

最多卖最多的天数时也是农民最早开始卖的情况了。

当卖50天时，那么100-50=50，50+1=51，从第51天开始卖。

1  2  3  4  5  6  7  8  9…47  48  49  50  51  52 53…91  92  93  94  95  96 97  98  99  100。

具体操作看上面等差数列，第51天卖50+51里的100个，第52天卖49+52里的100个，第53天卖48+53里的100个，第54天卖47+54里的100个，……第100天卖1+100里的100个，所以可以卖50天，每天卖100个，最早从第51天开始卖。

点评：方法1是整体构造法，很好。方法2：是根据等差数列的前后和不变来构造。也很好。

试题5：在4×4的方格网（如图）中，任选4个小方格染成黑色，构成轴对称图形的染色方法有多少种？

武汉童老师奥数分析：

关于a对称的有：4个在一行，对应4种。分布在2行，每行2个，先从4行中选择2行，有3+2+1=6种选择，选出来的2行，每行放2个，对应有2+2=4种放法，所以有6×4=24种放法。共4+24=28种放法。

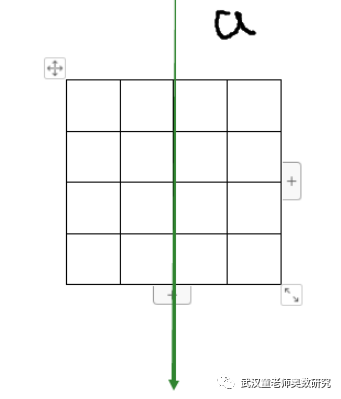
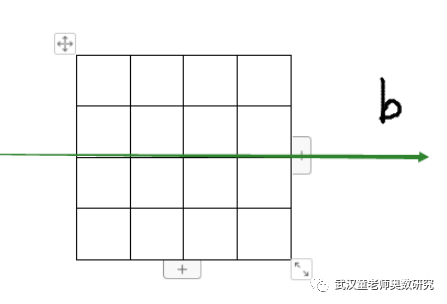
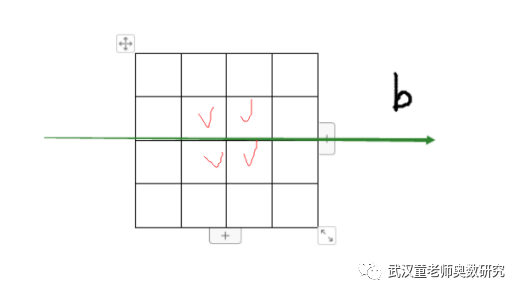
同理，关于b对称的有28种。

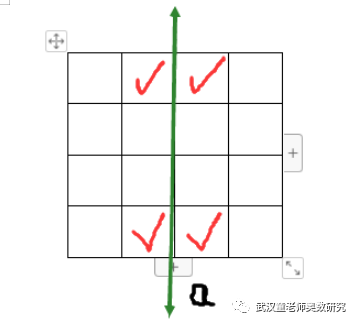
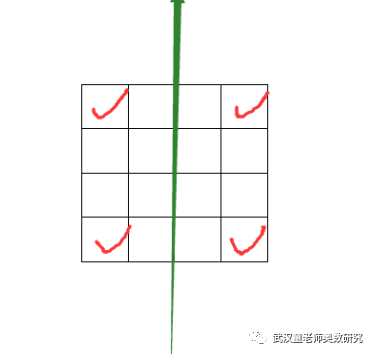
其中同时关于a和b都对称的有：4种。具体如下4种。

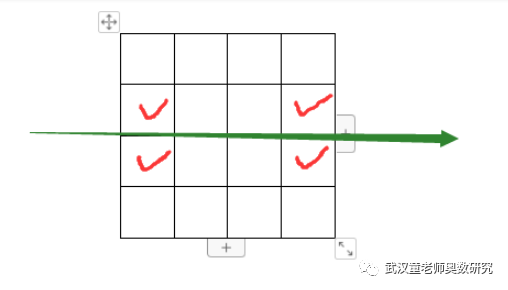
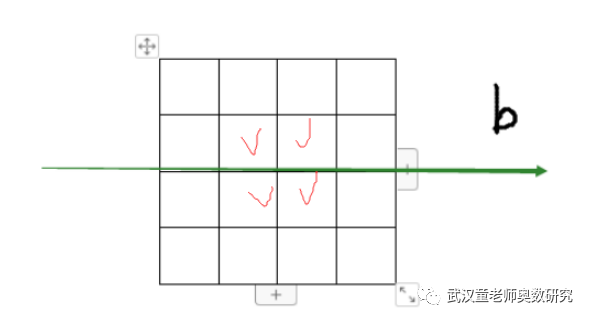
所以关于a和b对称的有28+28-4=52种。

关于c对称的有：

1、4个全在对称轴c上，1种；

2、4个中有2个在对称轴c上，另外2个在对称轴2侧，对称轴上2个有3+2+1=6种选择，两侧的2个有6种选择，所以有6×6=36种；

3、4个全都不在对称轴c上有：在c两侧有6组位置中选择2组有5+4+3+2+1=15种。

所以共有：1+36+15=52种。

关于d对称的有：同理也是52种。

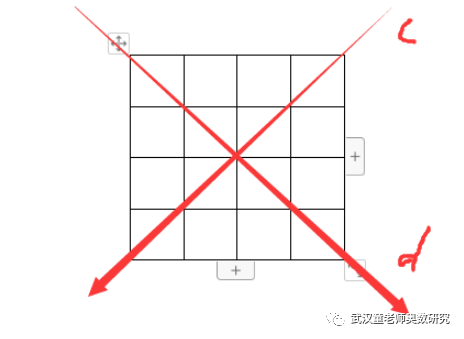
其中同时关于c和d对称的有：如下8种。

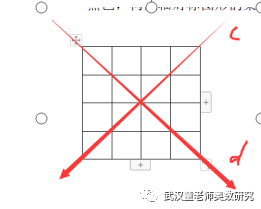
因为分成了四个区域，每个区域都有1个，在下面①和②位置对应有2种同时关于c和d对称的。

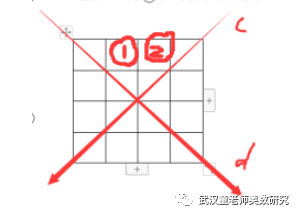
或者在下面③④⑤⑥中的任何2个位置也可以对应1种关于c和d对称的，所以有：③④、③⑤、③⑥、④⑤、④⑥，⑤⑥共3+2+1=6种。

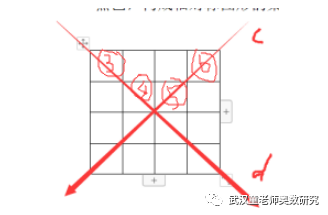
所以同时关于c和d对称的有2+6=8种。

所以关于对角线c或者d对称的共有：52+52-8=96种。

同时，关于对角线c或d且同时关于a或者b对称的有如下2种：

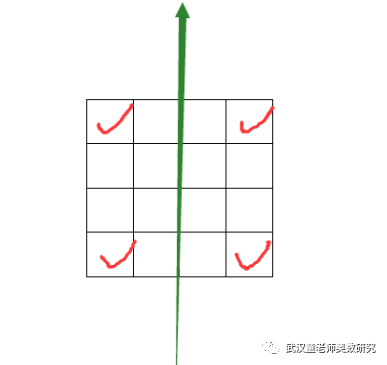
以上2种在关于a或者b对称的时候算过1次，在关于c或d的时候也算过1次，所以需要剔除掉。所以总的对称种数有：52+96-2=146种。

点评：分类计数综合题，难度很大。得全分很难。

试题6：有一个5×5的表格，其中每个小方格的变成为1（如图1）。

小华有8个1×2的“日”字形小块（如图2），小强有1块1×2的“日”字形小块。小华把8个“日”字形小块放入5×5的表格中，可以随便放，但是要求每个“日”字形小块恰好覆盖两个小正方形且互不重叠。问小强能不能把他的“日”字形小块放入表格中，且与小华放入的“日”字形小块不重叠？如果一定能，请说明理由。如果不一定能，请给出一种小华在5×5的表格中放小块的方式，使得小强一定不能把他的“日”字形小块放入表格中。

武汉童老师奥数分析：

小华把8个“日”放入5行，又因为每行最多放2个“日”字，所以8个分布在5行可以是：8=2+2+2+2+0或8=2+2+2+1+1。

接下来分类讨论：

（1）当8=2+2+2+2+0时，说明有1行空白的，小强把一个“日”放进去完全可以做到，

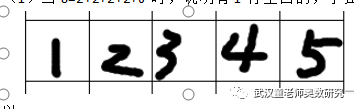
如上图可以选择在12、23、34、45位都可以；

（2）当8=2+2+2+1+1时，说明有存在某2行只有放1个（小华盖住了1个格子）。

如果盖住了1或5，小强可以放在23、34。如果盖住了2或4，小强可以对应分别放在45、12 。如果盖住了3，小强可以放在12或45 。

（3）所以小强可以把“日”字放进去，且与小华的8个“字”不重叠。

点评：构造和分类也可以理解是抽屉加分类探讨，真正竞赛题还是很需要构造能力哦。