2002年第9届“华罗庚金杯”少年数学邀请赛初赛试卷-参考答案与解析
一、解答题(共12小题,满分0分)
1.“华杯赛”是为了纪念和学习我国杰出的数学家华罗庚教授而举办的全国性大型少年数学竞赛.华罗庚教授生于1910年,现在用“华杯”代表一个两位数.已知1910与“华杯”之和等于2004,那么“华杯”代表的两位数是多少?
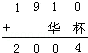
考点: | 竖式数字谜 |
专题: | 填运算符号、字母等的竖式与横式问题. |
分析: | 根据整数加法的计算方法进行推算即可. |
解答: | 解: 解法一: 个位上:0+“杯”=4,可得“杯”=4; 十位上:1+“华”的末尾是0,由1+9=10,可得“华”9,向百位上进1; 百位上:9+1=10,向千位上进1; 千位上:1+1=2; 由以上可得:
解法二: 已知1910与“华杯”之和等于2004; 那么“华杯”=2004﹣1910=94; 因此,“华杯”代表的两位数是94. |
点评: | 本题非常巧妙地考察了对整数的加法运算法则及数位的进位等知识要点的熟悉掌握程度. |
2.长方形的各边长增加10%,那么它的周长和面积分别增加百分之几?
考点: | 百分数的实际应用;长方形的周长;长方形、正方形的面积. |
专题: | 分数百分数应用题. |
分析: | 设长方形的长为a,宽为b,因此各边长增加10%时,则长为(1+10%)a=110%a,长为(1+10%)b=110%b,因此各边长增加10%时,周长增加2(1.1a+1.1b)﹣2(a+b)=2(a+b)×10%,即周长增加10%. 面积增加1.1a×1.1b﹣ab=1.21ab﹣ab=ab×21%,即面积增加21%. |
解答: | 周长增加10%,面积增加21% 解:设长方形的长为a,宽为b,边长增加10%时, 则长为(1+10%)a=110%a,长为(1+10%)b=110%b, 周长增加: 2(110%a+110%b)﹣2(a+b) =220%a+220%b﹣2a﹣2b =2(a+b)×10%; 面积增加: 110%a×110%b﹣ab =121%ab﹣ab =ab×21%; 答:周长增加了10%,面积增加了21%. |
点评: | 在求出长宽增加后的长度基础上,根据长方形的周长与面积公式计算是完成本题的关键. |
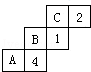
3.如图所示的是一个正方体木块的表面展开图,若在正方体的各面填上数,使其对面两数之和为7,则A、B、C处填的数各是多少?
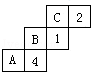
考点: | 正方体的展开图. |
专题: | 立体图形的认识与计算. |
分析: | 如图,是正方体展开图的“222”结构,把它折叠成正方体后,A面与1面相对,B面与2面相对,C面与4面相对,相使使其对面两数之和为7,A面填6,B面填5,C面填3. |
解答: | 解:如图,
折成正方体后,A面与1面相对,B面与2面相对,C面与4面相对, 要使其对面之各为7,则A面填6,B面填5,C面填3. |
点评: | 本题是考查正方体的展开图,关键是弄清把它折叠成正方体后,哪两个面相对. |
4.在一列数:1/3,3/5,5/7,7/9,9/11,11/13,…中,从哪一个数开始,1与每个数之差都小于1/1000?
考点: | 数列中的规律. |
专题: | 探索数的规律. |
分析: | 这列数的特点是每个数的分母比分子大2,分子为奇数列,要使1﹣ |
解答: | 解:这列数的特点是每个数的分母比分子大2,分子为奇数列, 1﹣ n>999.5,从n=1000开始, 即从 答:从 |
点评: | 找出这列数的规律,根据已知列出等式求解. |
5.“神舟五号”载人飞船载着航天英雄杨利伟于2003年10月16日清晨6时51分从太空返回地球,实现了中华民族的飞天梦.飞船绕地球共飞行14圈,其中后10圈沿离地面343千米的圆形轨道飞行.请计算飞船沿圆形轨道飞行了多少千米(地球半径为6371千米,圆周率π=3.14).
考点: | 有关圆的应用题. |
专题: | 平面图形的认识与计算. |
分析: | 先圆形轨道的半径,再根据圆的周长公式:C=2πr求出飞船沿圆形轨道飞行1圈的长度,再乘以10即可求出飞船沿圆形轨道飞行了多少千米. |
解答: | 解:2×3.14×(6371+343)×10 =2×3.14×6714×10 =3.14×134280 =421639.2(千米); 答:飞船沿圆形轨道飞行了421639.2千米. |
点评: | 考查了有关圆的应用题,关键是熟练掌握圆的周长公式. |
6.如图,一块圆形的纸片分成4个相同的扇形,用红、黄两种颜色分别涂满各扇形,问共有几种不同的涂法?
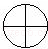
考点: | 染色问题. |
专题: | 传统应用题专题. |
分析: | 根据四个扇形中有一个红色、两个、三个、四个分类列举即可. |
解答: | 解:按逆时针方向涂染各扇形: 红红红红 红红红黄 红红黄黄 红黄红黄 红黄黄黄 黄黄黄黄 所以,共有6种. |
点评: | 本题考查了排列组合知识中的染色问题,还可以列式解答:4×(4﹣1)÷2=6(种). |
7.在9点至10点之间的某一时刻,5分钟前分针的位置与5分钟后时针的位置相同,此时刻是9点几分?
考点: | 时间与钟面. |
专题: | 时钟问题. |
分析: | 可设当前是9点x分,则5分钟前分针指向x﹣5的位置,而分针转动的速度是时针的12倍,分针5分钟后指向x+5的位置,时针指向9刻度后 |
解答: | 解:设当前时刻是9点x分.则5分钟后时针的位置为 45+ 540+x+5=12x﹣60 11x=605 x=55; 答:此时刻是9点55分. |
点评: | 本题主要考查钟表问题的实际应用,熟练掌握钟表的特征是解答本题的关键. |
8.一副扑克牌有54张,最少要抽取几张牌,方能使其中至少有2张牌有相同的点数?
考点: | 抽屉原理. |
专题: | 传统应用题专题. |
分析: | 建立抽屉:一副扑克牌有54张,大小鬼不相同,那么(54﹣2)÷4=13,所以一共有13+2=15个抽屉;分别是:1、2、3、…K、小鬼、大鬼,由此利用抽屉原理考虑最差情况,即可进行解答. |
解答: | 解:建立抽屉:54张牌,根据点数特点可以分别看做15个抽屉, 考虑最差情况:每个抽屉都摸出了1张牌,共摸出15张牌,此时再任意摸出一张,无论放到哪个抽屉,都会出现有两张牌在同一个抽屉,即两张牌点数相同, 15+1=16(张), 答:至少抽取16张扑克牌,方能使其中至少有两张牌有相同的点数. |
点评: | 此类问题关键是根据点数特点,建立抽屉,这里要注意考虑最差情况. |
9.任意写一个两位数,再将它依次重复3遍成一个8位数.将此8位数除以该两位数所得到的商再除以9,问:得到的余数是多少?
考点: | 带余除法. |
专题: | 余数问题. |
分析: | 先设这个两位数为10a+b,则可用含a、b的代数式表示将它依次重复写3遍成的一个8位数,再将此8位数除以该两位数得到商为1010101,然后将1010101除以9即可求解. |
解答: | 解:设这个两位数为10a+b,则将它依次重复3遍成的一个8位数为: 1000000(10a+b)+10000(10a+b)+100(10a+b)+10a+b=1010101(10a+b), 将此8位数除以该两位数得到的商为:1010101(10a+b)÷(10a+b)=1010101, 则1010101÷9=112233…4. 答:得到的余数是4. |
点评: | 本题考查了带余除法的定义及应用,难度中等,用含a、b的代数式正确表示将(10a+b)这个数依次重复写3遍成的一个8位数是解题的关键. |
10.一块长方形的木板,长为90厘米,宽为40厘米,将它锯成2块,然后拼成一个正方形,你能做到吗?
考点: | 图形的拆拼(切拼). |
专题: | 平面图形的认识与计算. |
分析: | 因为这块长方形木板的面积为90×40=3600(平方厘米),又因为3600=60×60,即所求的正方形的边长为60厘米,如下图所示. |
解答: | 解:因为90×40=3600,3600=60×60,所求的正方形的边长为60厘米,可以如下图拼成:
因此,能拼成一个正方形. |
点评: | 先求出总面积,看看是否能分成两个数的平方. |
11.如图,大小两个半圆,它们的直径在同一直线上,弦AB与小圆相切,且与直径平行,弦AB长12厘米.求图中阴影部分的面积(圆周率π=3.14).

考点: | 组合图形的面积. |
专题: | 平面图形的认识与计算. |
分析: | 将小圆缩小至0,则AB就是大圆直径,阴影部分就是大圆的一半,利用圆的面积公式即可求解. |
解答: | 解:将小圆缩小至0,则AB就是大圆直径,阴影部分就是大圆的一半, 所以阴影部分的面积是: ×3.14×(12÷2)2 =×3.14×36 =56.52(平方厘米); 答:图中阴影部分的面积是56.52平方厘米. |
点评: | 此题可以巧妙地利用“缩小法”,得出阴影部分的面积与直径为AB的圆的面积的关系,问题即可得解. |
12.半径为25厘米的小铁环沿着半径为50厘米的大铁环的内侧作无滑动的滚动,当小铁环沿大铁环滚动一周回到原位时,问小铁环自身转了几圈?
考点: | 有关圆的应用题. |
专题: | 平面图形的认识与计算. |
分析: | 由于小铁环的半径为25厘米,大铁环的半径为50厘米,可得小铁环的半径是大铁环半径的一半.根据周长与半径的关系可得大环周长是小环的2倍,即小环沿大环转2个周长时又回到原位,再减去公转的1圈,可得小环自身转动的圈数. |
解答: | 解:由于小铁环的半径是大铁环半径的一半, 所以大环周长是小环的2倍,即小环沿大环转2个周长时又回到原位, 其中有1个周长属于小环公转的,而另一个周长才是小环自身转动的, 因此,小环自身转动1圈. |
点评: | 本题考查了圆与圆的位置关系,小铁环运动的圈数乘以它的周长就等于大铁环的周长. |


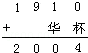
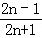 <
<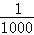 ,则n>999.5,即从n=1000开始,带入分数,即可得解.
,则n>999.5,即从n=1000开始,带入分数,即可得解.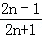 <,
<,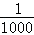
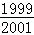 开始,满足条件.
开始,满足条件.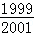 开始,1与每个数之差都小于
开始,1与每个数之差都小于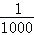 .
.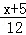 刻度处,根据题意列出方程解答即可.
刻度处,根据题意列出方程解答即可. =x﹣5
=x﹣5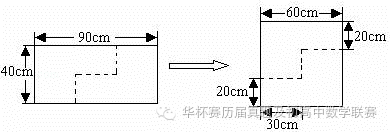


全部 0条评论