一、填空题（每小题10分，共80分）

1、在2017个自然数中至少有一个两位数，而且其中任意两个数至少有一个三位数，则这2017个数中有______个三位数。

思路分析点拨：此题考察分析能力，抓住重点语句“其中任意两个数至少有一个三位数”，即只有一个不是三位数，则三位数的个数是2017-1=2016.

2、如图[1]所示，一个棋子从A到B只能沿着横平竖直的路线在网格中行走，给定棋子的一条路线：将棋子在某一列中经过的格子数标在该列的上方，在某一行中经过的格子数在该行的左方。如图[2]中网格上方和左方的数字也是根据以上规则确定的，那么图中X代表的数字为______。

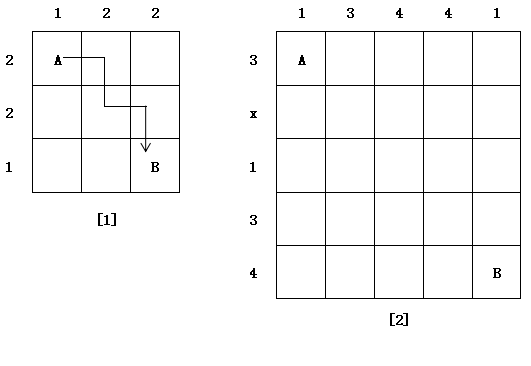
思路分析点拨：此题重点考虑第3行数字“1”，如下图，X=2.

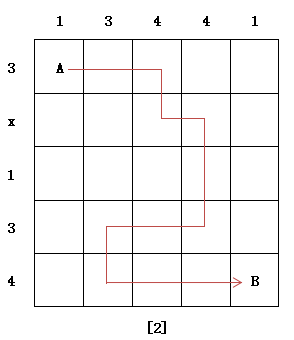
3、用[X]表示不超过X的最大整数，例如[10.2]=10。则 

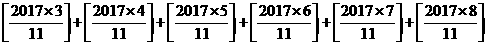
等于______。

思路分析点拨：此题可配对考虑，1和6，2和5，3和4，在不按运算“[]”时，每个配对和均为2017，而分子中2017与分母11均为质数，则每个分式都不能化成整数，则实际上每个配对的和为2017-1=2016，共3个配对组合，则原式子和为2016×3=6048.

4、盒子里有一些黑球和白球。如果将黑球数量变成原来的5倍，总球数将会变成原来的2倍。如果将白球数量变成原来的5倍，总球数将会变成原来的_____倍。

思路分析点拨：此题可用画线段图的方式，由“黑球数量变成原来的5倍，总球数将会变成原来的2倍”可知，黑球的（5-1）=4倍就等于原球数，则原白球是黑球的（4-1）=3倍，则白球扩大5倍的时候：黑球+白球×5=黑球+黑球×3×5=黑球×16，原总球数：黑球+白球=黑球×4，则16÷4=4.

5、能被自己的数字之和整除的两位数中，奇数共有_____个。

思路分析点拨：此题所求数为两位数并且是奇数，则个、十位数字和也必须为奇数，奇数中1、3、5、7、9、11、13、15、17中，首先1排除（两位数中没有数字和为1且是奇数的），其次5、11、13、15、17也不满足。在3和9中，只有21，27，45，63，81满足条件。即有5个。

6、如图，将一个正方形硬纸片的四个角分别剪去一个等腰直角三角形，最后剩下一个长方形。正方形边长和三角形直角边长都是整数。若剪去部分的总面积为40 平方厘米。则长方形面积是_______平方厘米。

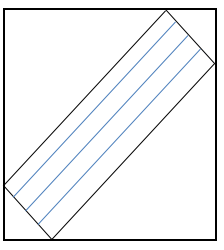
思路分析点拨：此题可将大小4个三角形分别合并组成2个正方形，则两个正方形的面积和为40.而40要分解成两个整数的平方和，只有唯一一种情况，即40=6²+2²，则原正方形的面积为（6+2）²=64，则长方形的面积为64-40=24.

7、小龙从家到学校的路上经过一个商店和一个游乐场，从家到商店距离是500米。用了7分钟；从商店到游乐场以80米/分钟的速度要走8分钟；从游乐场到学校的距离是300米。走的速度是60米/分钟。那么小龙从家到学校的平均速度是_____米/分钟。

思路分析点拨：此题考察计算能力。（500+640+300）÷（7+8+5）=72.

8、亚瑟王在王宫中召见6名骑士，这些骑士中每个骑士恰好有2名朋友。他们围着一张圆桌坐下（骑士姓名与座位如右图），结果发现这种坐法，任意相邻的两名骑士恰好都是朋友。亚瑟王想重新安排座位，那么亚瑟王有______种不同方法安排座位。使得每一个骑士都不与他的朋友相邻（旋转以后相同的，算同一种方法）。

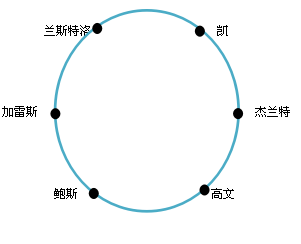
思路分析点拨：此题为方便起见可用数字替代人名，即6人分别为1-2-3-4-5-6，可假设1的朋友为2和6，2的朋友为相邻的1和3，依次类推。那么以1为基准可排的座位顺序如下：

1，3，5，2，6，4；

1，4，6.，2，5，3；

1，3，6，4，2，5；

1，5，2，4，6，3；

1，4，2，6，3，5；

1，5，3，6，2，4。

共计6种。

二、简答题(每小题15分，共60分，要求写出简要过程）

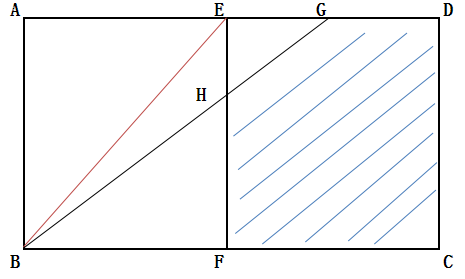
9、如图所示：两个边长为6的正方形ABFE和CDEF拼成长方形ABCD。G为DE的中点。连接BG交EF于H。求图中五边形CDGHF的面积。

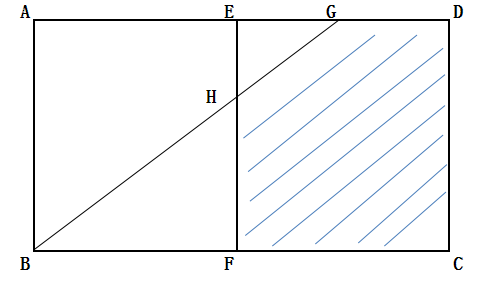
思路分析点拨：可连接B、E，在△BEG中，S△BEG=EG×AB/2=EH×（AE+EG)/2，可知EH=2，则S五边形=S正方形EFCD-S△EHG=36-3=33.

10、乌龟与兔子进行1000米赛跑，兔子速度是乌龟速度的5倍，当他们从起点同时出发后，乌龟不停地跑。兔子跑到某一地点开始睡觉，兔子醒来时乌龟已经领先它。兔子奋起直追。但乌龟到达终点时，兔子仍落后10米。求兔子睡觉期间，乌龟跑了多少米？

思路分析点拨：此题与原题库的题型一致。请点击：小学竞赛习题解析分享。1000-（1000-10）÷5=802.

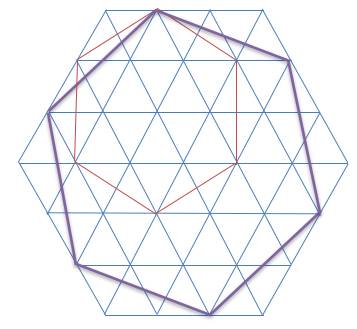
11、如图，一个边长为3的正六边形被3组平行于其边的直线分割成边长为1的54个小正三角形，那么这些小正三角形的顶点为顶点的正六边形共有多少个？

思路分析点拨：此题满足条件的正六边形可分五种情况考虑：

边长为1的正六边形有：3+4+5+4+3=19个；

边长为2的正六边形有：2+3+2=7个；

边长为3的正六边形有：1个；

边长为红线的正六边形有：2+3+2=7个；

边长为紫线的正六边形有：1+1=2个。

合计：19+7+1+7+2=36.

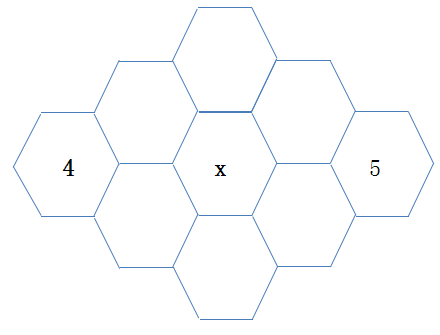
12、如图，将1至9这九个数填入网格中，要求每个格子填一个数字，不同格子填的数字不同，且每个格子周围的格子（即与该格子有公共边的格子）所填数字之和是该格子中所填数字的整数倍。已知左右格子有数字4和5，那么标有字母x的格子可以填的数字最大是多少？

思路分析点拨：此题首先考虑X周围6个格子的数与X之间的和：45-4-5=36。而X必定是36的约数，在1-9中，有1，2，3，4（舍去），6，9。分情况讨论如下：

（1）当X=9时，可从右边数字5先考虑，5左边的两个格子和可能是5，10，15，

5=1+4（舍）=2+3

10=1+9（舍去）=2+8=3+7=4+6（舍去）

15=6+9（舍去）=7+8

分析过后逐一舍去；

（2）当X=6时，数字5左边当有且只有2+8时成立。即如下图：

当然6上方3格与下方3格可对调。