什么是华杯赛？

今年是华杯赛的第23届，历经23年，它已经不单是北京的考试，早已上升为全国性的数学竞赛，华杯赛决赛的舞台上，大家将和来自全国各地的数学天赋较高的同学们同场竞技，所以华杯赛相对于其它联赛如希望杯、迎春杯、K6联赛等来说，含金量更高，更受到中小学名校的认可，尤其是在我们洛阳，一外、二外、地调等名校会提前在华杯赛获奖者中择优选拔。

相对于其它竞赛，华杯赛流程更简单一些，分为初赛，决赛，总决赛。因为今年18年是偶数年，最后会在两岸三地大陆和港澳台进行国际精英赛。

而我们洛阳小升初的选拔，主要以决赛的成绩为准，所以在决赛中拿奖，则成为参赛同学们的最主要目标了。

在初赛进行前一周，华杯赛官方网站会公布一道题，称为公开题，公开题在初赛考试中一定会出现，题干也完全相同，供考生们先睹为快。

12月9日，迎春杯后一周进行。

与迎春杯不同的是，华杯赛三四年级统一称为中年级组，五六年级统一称为高年级组，两组分别考试。

考试试卷一共10道题，每道题目10分，前6道题是选择题，后4道填空题。不论是选择也好还是填空也好，都是按结果给分，只要做对了题目分数就拿到了。

考试共60分钟，考试时间相对来说还算比较充裕，平均一道题6分钟，再加上10道题中有一道是公开题，如果这道题同学们已经掌握的话，那相当于只有9道题，60分钟考试时间，而初赛进到决赛的比例是35%，也就是三分之一的同学能够进入到3月份的决赛当中。

那究竟什么样的水平能够进入决赛呢？从往年情况来看，一般是40～50分左右能够进入决赛，也就是说我们在考试中要做对 4～5道题基本能够通过初赛进到决赛。

之前决赛只有高年级组，12年开始，中年级也加入进来。14道题，满分150分。

14道题划分为3个部分，第一部分填空题，8道题80分；第二部分简答题，要求不能光填空，必须写出简要过程，4道题40分；还剩下两道题，叫做解答题，必须一步一步写出思考过程，每道题目15分。

华杯赛规定：获决赛个人一、二、三等奖比例为本市参加决赛人数的36%。其中：一等奖为参加决赛人数的6%，二等奖为参加决赛人数的12%，三等奖为参加决赛人数的18%。

分为两部分，第一部分个人笔试，根据个人笔试成绩取得团体名次，然后进行团体考试，最后进行加分和减分。不管是偶数年精英赛也好，还是奇数年的金杯，都代表着小学数学学习最高的荣誉，不管是哪个年龄段，数学学得非常好的同学们的同场竞技，所以如果真的是获得这个奖项的话，代表着你在相应年级段已经具备全国相当高的水平。

华杯赛考什么？

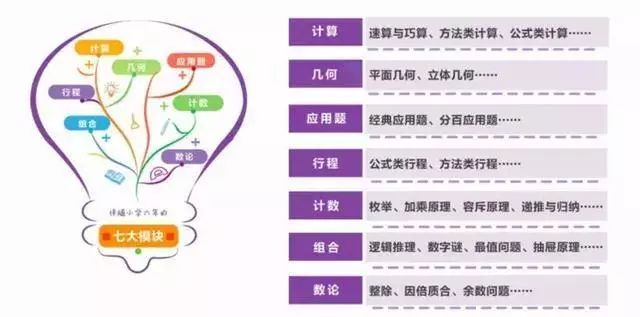
图中列出了涵盖小学数学六年知识点七大模块，分别为计算，几何，应用题，行程，计数，组合，数论。

不同年龄段涉及的知识点是不同的，但整个来说是以进阶的方式进行。同学们根据模块复习，看看自己哪个模块哪个知识点不太牢固，复习会更缜密。

小学中年级组

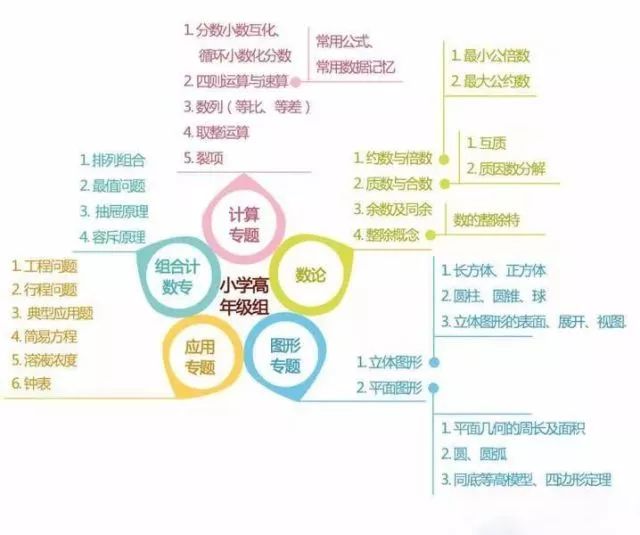
小学高年级组

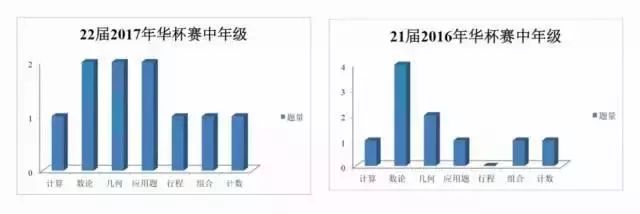
以近两年考点分布为例，分析备考方向，先看中年级，17年考的很均衡，每个知识模块都有考到，再看16年，我们会发现华杯赛是个很强调数论的比赛，甚至整个试卷一半左右的题目的会考到。虽然在17年几何和应用的比重也有所上升，但在决赛中数论依然会占到它应有的比重。

除了数论，还有几何也应该注意下。几何的题量是降不下来的，2道题已经是底线。所以在中年级准备上，备考重点一个是数论，一个是几何。所以建议大家把这两个模块当时的作业，小测等题目拿出来再看看还有哪些漏洞。

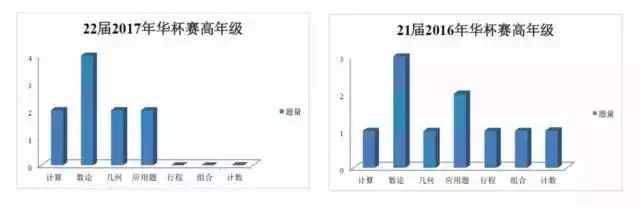
再来看高年级近两年题目考点分布。16年考点也是挺均衡的，各个考点都有考到，17年7大模块只剩下4大模块。所以凸显了计算，数论，几何，应用题这四个重点，其中数论依然是重中之重。

从近两年的试题分布可以看出，华杯赛初赛和决赛的考察重点基本都在数论、几何、组合三个模块，占据总分值的70%左右。

通常压轴题会在数论或者组合杂题中出，当然这几个模块也不会都是难题，华杯赛对于试题难度的划分非常明确，对基础题、中等题、高难度题整体比例有严格的规定。初赛中基础题、中等题、高难度题整体比例为4:4:2；决赛中三类题型的整体比重为4:6:4。

基础题、中档题比重超三分之二！如果能将基础题和中档题全部做对，或者大部分做对，在华杯赛中得奖是绝对没问题的。如果想拿一等奖，那对于数论和组合杂题这两个模块应该着重下功夫学习研究。

分析过后，我们再看一下最近五年来各模块所占比例的变化趋势：

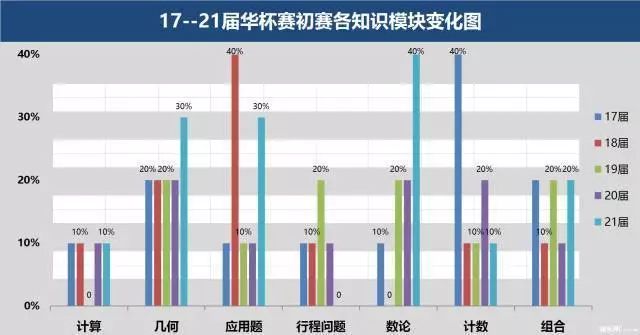
通过对近五届初赛的统计，可以看出，在初赛中，各模块所占的比例大致上处于稳定的状态，只有数论部分在持续的增多，这也反应出数论部分越来越受到出题人的青睐。所以在后面的备考中一定要抓住重点，知己知彼。

通过对近五届决赛的统计，可以看出在决赛中，计算、应用题、行程三个模块的变化不大，计数模块略有增多，而几何模块却在持续增多的状态，反而组合杂题模块越来越少，一直处于大头的数论模块略有增多的趋势。总的来说，依然是数论、几何、组合杂题三个模块所占比重最大，而且对于几何和数论的考察有增多的趋势。

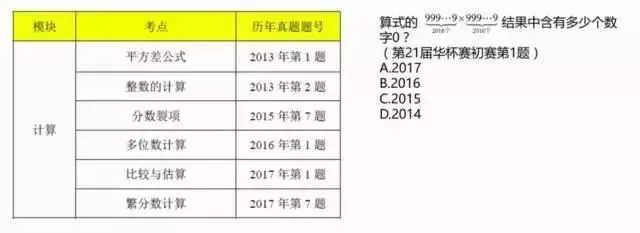
计算模块历年考情

右边例题为16年初赛第1题，大数计算。数太大，算肯定是不现实，那应该怎么办呢？如果不知道方法，我们可以试试9×9，99×99，观察下0的数量和9有什么关系。当你基础比较薄弱，知识点掌握不太好的时候，就可以通过这种方法尝试下。可能当你写出9，99，999时大概就能判断出答案了。

这种方式什么时候用的比较多呢？就是和年份相结合的时候。我们会发现但凡出现和年份结合的时候，因为数量非常多，没办法真的算出来，所以通过从小到大找规律的方法试一试，这是很实用的一种方法。

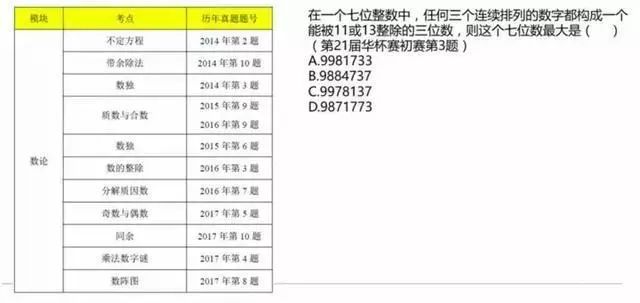
数论模块历年考情

右边例题为16年公开题。这个题考的可能是11或13的整除特征。很明显是差系。但要注意的是要求是三位数。我们会发现这个不好办，因为我们是从末尾三位数三位一个，另外一个点差系有一个数很重要，1001＝7×11×13。所以我们知道1001即是7的倍数，又是11的倍数，又是13的倍数。想找最大的7位数当然希望高位尽可能的大，最大又最接近999的话，那用1001-11=990或者1001-13=988，所以前三位要么是990，要么是988，四个选项看下发现只有B可能是对的，那我们代入验证后发现答案就是它。所以你会发现，选择题好做的原因就是答案可以根据题目条件代入验证。

数论考点很多，一定要好好回顾。高年级相对好一些，数论学的比较久。低年级尤其要注意一下。

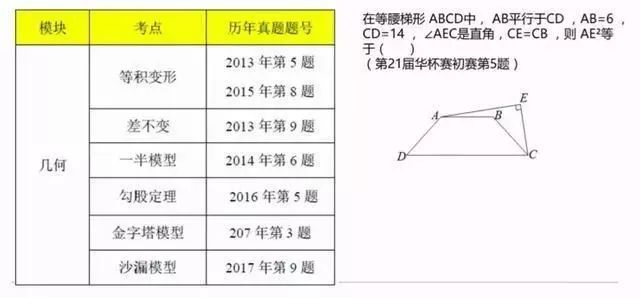
几何题模块历年考情

几何题小学阶段更多的考查的是面积，而右边例题考察的是边长的平方。延伸思考下，平方和什么有关系呢？勾股定理，那么解题思路很容易就出来了。

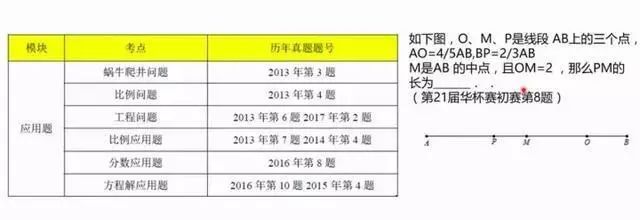
应用题模块历年考情

中年级考核会非常多，填空题不见得非常难，我们要好好想想题目对应的是哪个知识点，用以前学过的哪个方法来解。

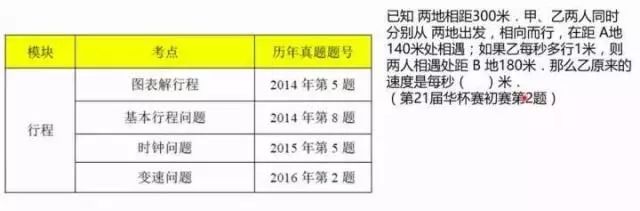
行程题模块历年考情

行程问题是公认的难度比较大的题目，我们可以发现，行程在华杯赛中考的频次不算特别高。这个题是很直接的比例行程问题。先求甲乙速度比，找到不变量，根据不变量解决问题。

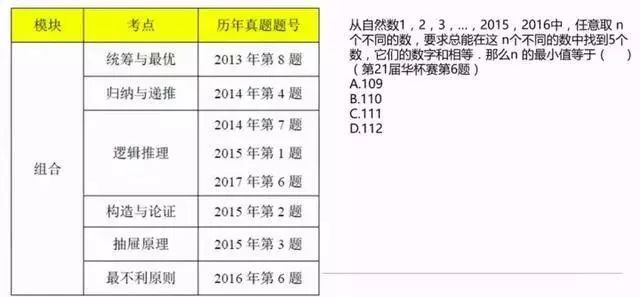
组合模块历年考情

组合题如果出现的话，难度应该偏大一点。右侧例题从“总能”我们可以看出这道题考的是最不利原则。可以先看看数字和为1的情况，数字和为2的情况，再想想数字和最大的情况呢？最不利原则一定是先找到符合情况的最大值，在加上一个，一定就是能够实现最终目标的答案。

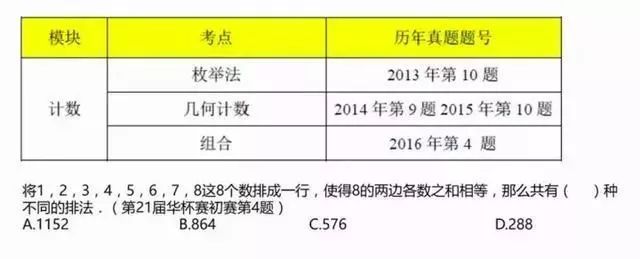
计数模块历年考情

例题很明显是加乘的问题。1-8数字和是36，1-7的数字和是28，说明8两边分别是14，先把8两边的数分成两组，分好组后会发现共有4种不同分法，再根据左右两边可以交换，得到8种分法。左边三个右边四个或者左边四个右边三个都可以排列，得到最终结果。

解题技巧来啦！

读懂题 ➜ 会做题 ➜ 算对题

❶ 先要读懂题，知道题目是什么意思

❷ 能把题目读懂后，知道用什么方法解决

❸ 不但会做还能算对，像上面计算例题，数字很大但依然能保证算对。

不管是平时数学学习，还是备战杯赛期间，这是需要同学们尽量努力提升的3个部分。

公开题 ➜ 得分题 ➜ 用方法的题

❶ 先做公开题，带着答案去做的。既然已经明明白白告诉你题目了，就一定要尽力把题目搞懂弄清楚白送的分数一定要拿到。公开题很快解决后，你会给自己建立起信心，我接下来的时间大概做对4～5道题就能很稳妥的保证进入决赛。

❷ 再做的分题，也就是看上去就很熟悉的认真想一下能够答出来的题目。

华杯赛初赛难度设置其实不高。10道题分为三档，简单题，中等题，难题，比例是4:4:2，4道简单题，4道中等题，2道难题。也就是说，除了公开题外，还有3～4道简单题是一定可以拿到分的。

所以考场上，先找到这几道简单题，看看属于哪个知识模块，好好思考解决一下。

❸ 如果时间充足，前面的两步完成较好，中档题也是可以尝试冲一下的，能够用很多方法去尝试，比如方程法，大胆推测法等。比如几何题用量，选择题答案带回题目中验证。这就是为什么说选择题更好做呢？因为它们提供了更多的条件，给的答案中一定有一个是对的，那你就可以往题里代。

根据自身选择目标

在竞赛中，针对自己的实际数学水平，可以定3种不同的目标：

1、如果平时数学学习一般，那只要参加了竞赛，尽自己最大的努力就可以了，感受竞赛的气氛，通过接触那些有挑战性的试题，使自己开阔了眼界，激发了钻研的兴趣，这是最重要的。

2、如果平时数学学习比较好，通过初试，能够进入决赛就达到目标，主要是通过竞赛看看自己的能力和掌握的知识还有什么不足。

3、数学水平较好的同学，目标就是争取夺得奖牌，通过竞赛主要是查漏补缺，总结经验教训。

不同年级，对比赛的期望也有所不同。

★ 对于5年级，主要是锻炼自己心理状态，能够不畏惧，敢于应考，为以后参加其他考试炼胆量、炼能力；

★ 对于6年级，初次参赛的应该是锻炼自己为主，第二次参赛的同学目标就要稍微高一些；只要在赛前给自己设定了预定的目标，考试时就不会紧张，更不会出现由于心理不稳定发挥失常。