华杯赛题，特别是复赛和决赛试题的含金量是很高的，其中有相当一部分题是非常好的原创题，极俱思考性。这源自华杯全国组委会有一个强大的试题原创团队，其成员组成非常丰富，有数学家，有大学数学教授，也有一线小学老师和教练。华杯赛题以思维考核著称，考量参赛者面对新问题的数学思维能力，活学活用，有独立思考独创思路的聪明孩子往往能脱颖而出。

  第二题   几何

       原题

       如图CEB三点共线，CB⊥AB，AE∥DC，AB=8，CE=5，则△AED的面积为多少？

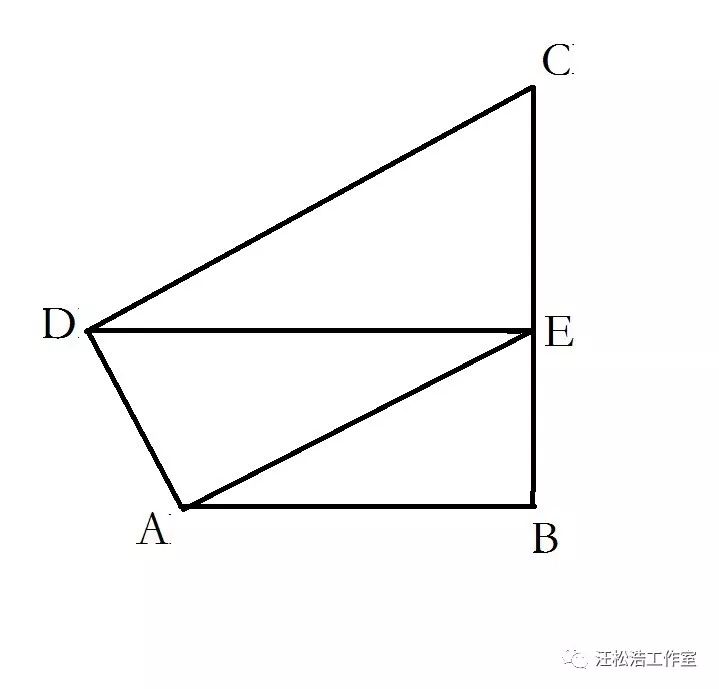
    审题：

    几何类型的审题，最好能把已知条件在图形上走一遍，能标注的标注，形成目视能及的条件综合感观。

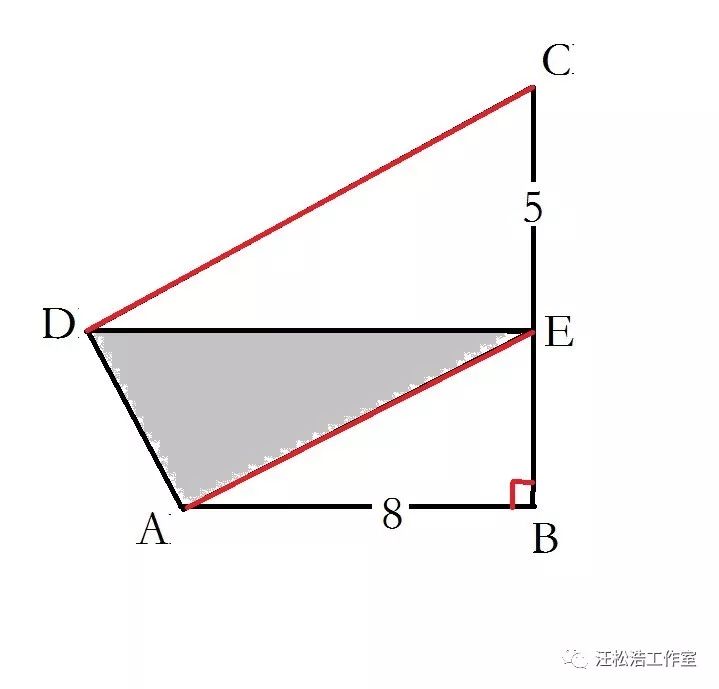
请独立思考之后再继续阅读！这很重要！

     分析:

     △AED的面积，不可直接计算，直接关联的条件显然不够。在面积不可直接求出的时候我们往往有两个思路：

      1、将图形分割或转化为等面积的其他图形求出；

      2、用总面积减去其他空白部分面积求出。

       三角形面积需要“底”和“高”两个条件，而原题条件中有“垂直”条件一个，显然跟“底”和“高”关联。可惜的是这两个条件不在同一个已知三角形内。于是我们必须拿出几何体的杀手锏--作辅助线构造一个三角形可用。

     构造：

      在求面积的几何题中我们往往用“等积变形”来构造需要的三角形。我们现在需要在△AED和条件“AB=8，CE=5”之间搭建一个“桥梁”来实现沟通。那么我们该作辅助线来构造一个新三角形，这个三角形必须跟两者都有关联（否则就不叫桥梁了），它必须是以“8和5”为高和底的三角形，同时和△AED的面积直接关联最好是面积相等的。

        于是：我们可作辅助线AC。得“桥梁”△ACE。因AE∥DC，所以S△ACE=S△ADE。

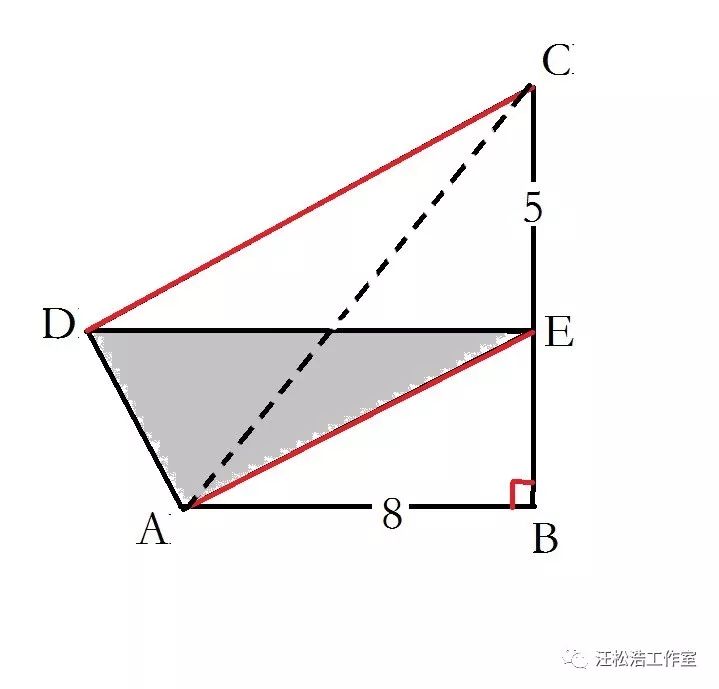
    解法：

    S△AED=S△ACE=5×8÷2=20

    附录：

    三角形等积变形：

    三角形的面积公式为：底×高÷2，故只要底和高相等的三角形面积都相等，那么不同三角形共底、等高，它们的面积都相等。等高的三角形往往可以在两条平行线中间找到，等底往往在边的平分线上找到。

     同时，若不同三角形的高和底有确定的倍数关系，面积也会有相应的乘积倍关系。

      试试在下面的图形中找到“等积”的几何图形。

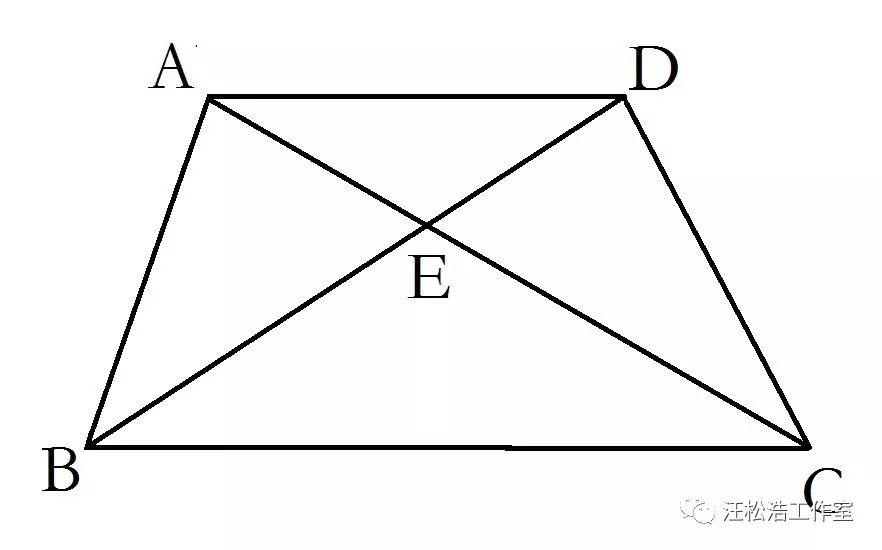
       等积变形中有经典的等积模型：燕尾模型、漏斗模型、蝴蝶模型。孩子们可以去找相应的题目解答并体会。

       自然，每一个相关的知识点的背后都是一个系统的认知做支撑的，希望孩子进行系统训练之后再做提高思考。汪师的析题，都应该是你做好了知识储备之后帮助你往更高出走的提携，希望孩子能不断突破自己的思维极限，迈向更广阔的数学天地。