【希望杯、华杯赛、迎春杯】历年真题汇编——数论篇

0 人点赞了该文章 · 249 浏览

三大杯赛简介

“迎春杯”：“迎春杯”是北京市的一项传统中小学赛事，开始于1984年。2013年更名为”数学花园探秘"科普活动。“迎春杯”数学竞赛对激发学生学习数学的兴趣，发现优秀的数学特长生，推动北京中、小学数学教学改革等方面都起了很大的作用。

“华杯赛”：华罗庚金杯少年数学邀请赛，于1986年创始，是全国性的大型少年数学竞赛活动。“华杯赛”一贯坚持普及性、趣味性、新颖性的命题原则，是全国规模最大的中小学数学比赛。

“希望杯”：“希望杯”全国数学邀请赛创始于1990年，每年一届，以激发广大中学生学习的兴趣，培养他们的自信，不断提高他们的能力和素质为宗旨。

资源介绍

虽然杯赛已经被禁止，但是往年杯赛的题目有重要的参考价值，其题目质量高、出题范围广，是众多小升初考试和分班考试的题目来源。

方田教研团队把15年到17年三大杯赛的考试题目做了综合汇编，分成七大模块陆续分享给大家，并做部分经典题目的试题讲解~

本期整理的内容是数论模块，包含30页共119个题目，涵盖了15-17年希望杯、迎春杯和华杯赛所有年级初赛和复赛所有版本的数论问题~

本期杯赛题型：短除模型

短除模型是数论模块中非常重要又常用的解题模型，主要涉及到两个数和最大公因数及最小公倍数之间的关系。

短除法是简化了除法竖式的计算方法，为了方便书写，演变为现在常见的短除符号。短除法也常用于分解质因数。

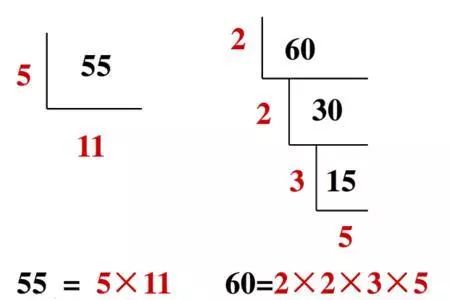
“华杯赛”真题精选

2015年华杯赛小高组A卷决赛第9题

短除模型解题技巧

短除模型如下

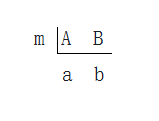
重要结论：

A=ma，B=mb，A+B=ma+mb=m(a+b)

m 为 A 和 B 的最大公因数，表示为(A,B)；mab 为 A 和 B 的最小公倍数，表示为[A,B]。

A×B=ma×mb=m×mab=(A,B)×[A,B]

题目中提到最大公因数和最小公倍数时，应首先想到短除模型解题。

试着做一做