题目评析：第一阶段题目灵活使用假设法，找矛盾对立和统一以及列表格能够完成；不需要额外更多知识点，题目逻辑性很强，同一背景，往往前面一小题对后面一小题有提示作用。

1、每组题目由易到难。1-5题，第1题，利用基本要求排除顺序和要求矛盾选项，第2、3小题给出几个表演顺序，补充剩余小狗顺序，第4、5小题涉及更多分类讨论，灵活运用给出的条件解决问题。

2、小题之间紧密联系。所谓没有无缘无故的爱，没有无怨无故的恨，也没有无缘无故的第一小问。第7题铺垫第8题小赵一定有猴子P，第8题猴子Q分给小李当做结论又是第9题的基础，环环相扣，层层递进。第12小题铺垫第13小题的循环周期。

难度：1-3星

二．填空题（本大题样题全选自迎春杯往届试题）

（第 16、17 小题各 9 分，第 18、19 小题各 12 分，第 20 小题 18 分，共 60 分）

16．如图，有编号 1～9 的 9 个小正方形狗舍，每个狗舍至多住 1 只小狗；原有 3 只小狗，它们 所在的狗舍互不相邻（相邻的小正方形有公共边）；当有新的小狗入住时，与之相邻的小狗就 会吠一声表示欢迎；现在又先后依次新入住 5 只小狗，每只小狗入住时都

恰好有 2 只小狗吠一声；已知第 1 只新入住的小狗住 2 号狗舍，第 2 只新 入住的小狗吠了 2 声，第 4 只新入住的小狗住 4 号狗舍，它没吠过；设这 5 只先后新入住小狗所住狗舍号依次为 A、B、C、D、E，那么五位数ABCDE＝_______．

1	2	3
4	5	6
7	8	9

【答案】25649   

【解析】为方便描述，原来三只称原住狗，新来的称新1狗，新2狗....新5狗,已知A=2,D=4；

①小狗入住都恰有2只小狗吠，新2号住进之前旁边有2条小狗，新2号小狗吠了两声，说明后续在它旁边进来两只小狗，所以新2号至少和4条狗相邻，只有5号狗舍，B=5；

②新1号小狗住2号狗舍，且5号狗舍是新2狗，那么1号和3号狗舍是原住狗，新2入住前有2只狗吠，6号一定不是原住狗（否则原住狗相邻），则8号是原住狗

③显然，6号狗舍是新3狗，C=6;9号狗舍是新5狗,E=9

则

 

17．陈老师告诉甲,乙,丙各一个数后，四人依次有如下对话．

陈老师说：“这三个数是 1～9 中互不相同的自然数，丙的数恰好是甲、乙的数的平均数，

你们现在都只知道自己的数，请你们猜测其他人的数．”

甲说：“我猜丙的数是 7．”

乙说：“丙的数不可能是 7，我猜丙的数是 6．”

丙说：“现在只有乙还在猜，我和甲已经全知道了．”

假设他们都足够聪明且诚实，甲,乙,丙拿的数顺次组成的三位数是__________．

 【答案】645   

【解析】数学华夏四年级7

①丙的数恰好是甲、乙的数的平均数，丙=（甲+乙）÷2，甲乙同奇偶（否则有小数）

②甲：我猜丙的数是 7。  则甲+乙=14，甲不是1,2,3,4,7，可能是5,6,8,9

乙：丙的数不可能是 7，我猜丙的数是6．  则乙不是5,6,8,9，猜丙是6，则甲+乙=12，1-9中，3+9=4+8=5+7=12，由于乙不是5,6,8,9，则乙可能是3,4,7

综合①，②，甲的数是5或9，此时乙是3或7；甲的数是6或8，此时乙是4

③丙说：“现在只有乙还在猜，我和甲已经全知道了．”甲知道了，则甲不是5或9（否则乙不确定），则确定甲是6或8，乙是4，则丙手里是5或6。

丙也知道了，若丙手里是6，则甲+乙=12=3+9=4+8=5+7，无法确定甲和乙，若丙=5，则甲+乙=3+7=4+6，显然3和7只有乙可能拿到，舍去。由此，则甲=6，乙=4，丙=5.

 

 

18．老师将写有 1~5 的 5 张卡片分别交给 1~5 号同学，每位同学聪明且诚实，拿到的卡片上的数字和自己的编号不同．如果 A 同学告诉 B 同学自己的卡片数字后，B 能够推出所有人的卡片数字，则称 A 是 B 的“线人”．老师悄悄告诉 1 号同学谁拿了 1 号卡片后，5 位同学进行了如下交谈：

1号同学说：“现在 2 号同学是我唯一的线人．”

2号同学说：“这样说来，现在 3 号同学是我唯一的线人．”

3号和4号同学异口同声地说：“那我不需要线人已经知道你们所有人的数了．”

那么，1~5 号同学拿到的卡片数字顺次组成的五位数__________．

 【答案】23514

【解析】

1号同学说：“现在 2 号同学是我唯一的线人．”1号一定知道2号的特殊信息，显然是1号手里拿到2号卡片（否则不是唯一线人）

2号同学说：“这样说来，现在 3 号同学是我唯一的线人．”显然，是2号手里拿到3号卡片；此时3,4,5号人手里卡片有3种可能：154,451,514（列表格更容易看明白）

卡片	1	2	3	4	5
人	2	3	1	5	4
			4	5	1
			5	1	4

 

3号和4号同学异口同声地说：“那我不需要线人已经知道你们所有人的数了．”3号必定拿5，否则无法判断4号，4号人手里拿1，否则无法判断3和5号人，那么5号人手里拿着4，无法判断3和4号的卡片。

综上：23514

 

19． 老师用 0 至 9 这十个数字组成了五个两位数，每个数字恰用一次；然后将这五个两位数分别

给了 A、B、C、D、E 这五名聪明且诚实的同学，每名同学只能看见自己的两位数，并依次

发生如下对话：

A 说：“我的数最小，而且是个质数．”

B 说：“我的数是一个完全平方数．”

C 说：“我的数第二小，恰有 6 个因数．”

D 说：“我的数不是最大的，我已经知道 A、B、C 三人手中的其中两个数是多少了．”

E 说：“我的数是某人的数的 3 倍．”

那么这五个两位数之和是__________.

 【答案】180

【解析】

A 说：“我的数最小，而且是个质数．” A可能是13,17,19，必定有数字1

B 说：“我的数是一个完全平方数．”25，36,49,64

C 说：“我的数第二小，恰有 6 个因数．”则可能是20,28或32；必含有2，B不是25

D 说：“我的数不是最大的，我已经知道 A、B、C 三人手中的其中两个数是多少了．” 确定自己不是最大，则十位小于等于5，

E 说：“我的数是某人的数的 3 倍．”显然可能是13,17,19,32的3倍。若E=96，则B不成立E=39,3重复使用，E=51,1重复使用

则E=57，A=19，

D知道 A、B、C 三人手中的其中两个数是多少了，BCD手中数可能为36,20,48或36,28,40，

和=19+36+28+40+57=19+36+20+48+57=180

 

 

20． 小明和 8 个好朋友去李老师家玩．李老师给每人发了一顶帽子，并在每个人的帽子上写了一个两位数，这 9 个两位数互不相同，且每个小朋友只能看见别人帽子上的数．老师在纸上又写了一个数 A，问这 9 位同学：“你知不知道自己帽子上的数能否被 A 整除？知道的请举手．” 结果有 4 人举手．老师又问：“现在你知不知道自己帽子上的数能否被 24 整除？知道的请举手．”结果有 6 人举手．已知小明两次都举手了，并且这 9 个小朋友都足够聪明且从不说谎， 那么小明看到的别人帽子上的 8 个两位数的总和是__________．

 

【答案】438

【解析】

一个人不知道自己帽子上的数是多少，却能知道自己帽子上的数能否被A整除，有两种可能：第一种可能，A的倍数中的两位数都出现在其他人帽子上，自己与其他人数不同，一定不是A的倍数。第二种可能不是A倍数都出现在其他人帽子上，判断自己一定是A倍数

①能否被A整除，有4人举手，显然5个人不可能包含所有不是A倍数的情况，因此只能是举手的人看到了5个A的倍数，5A＜100，6A≥100，则A=17,18,19

②第二轮举手，刚才没举手的5个人能够判断出自己分别是A,2A,3A,4A,5A,显然这5个人可以判断出自己的数具体是多少。

③小明第二次也能判断出自己是不是24的倍数，说明他看到了24的两位倍数：24,48,72,96有3个数出现在别人头上，显然A必然等于18，第一轮没举手的5个人分别是：18,36,54,72,90，第二轮没有举手的三人分别是24,48,96，

小明看到的8个两位数的和是:18+36+54+72+90+24+48+96=438

 

 题目评析：迎春杯真题往往需要很强的逻辑，基本考察的都是数论和逻辑的结合，涉及很多基础知识，想要做好这一部分，需要梳理好数论基本知识逻辑体系，了解因数倍数，质数合数，最大公因最小公倍基本概念，尤其是质数合数。

数论类逻辑推理本质是枚举，排除合理可能。

难度：4-5星

附一个数论思维导图

---

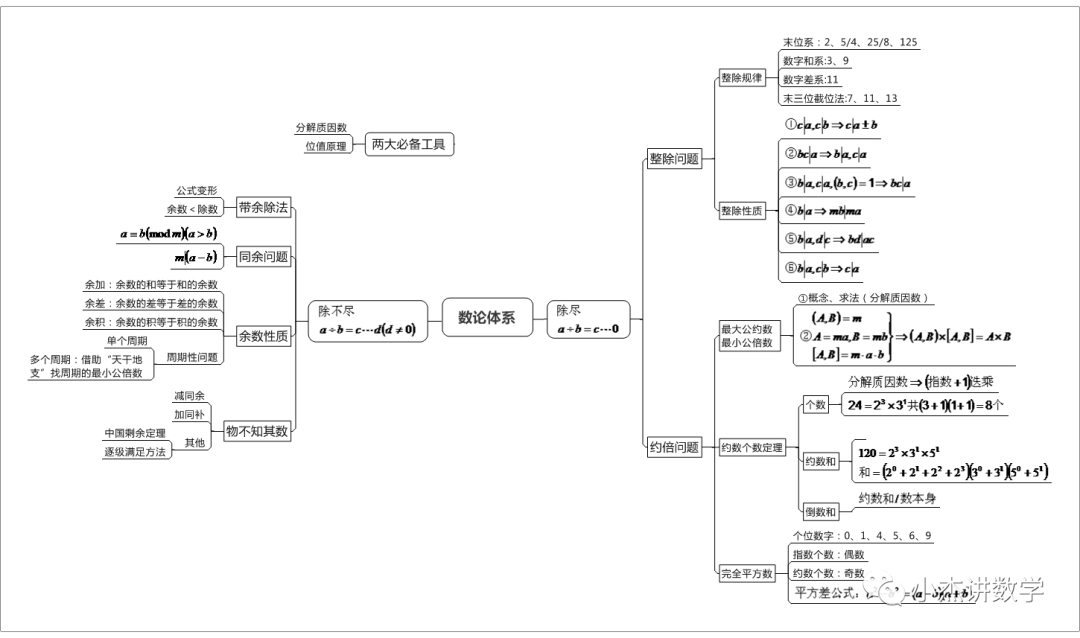
② 知名机构人大附早早培（zzp）学前集训队-数学/神测和动手

① 华杯赛/华数之星真题试卷-解析版 附详细解题过程

② 迎春杯/青少年创新能力测试-解析版 附详细解题过程

③ 希望杯/希望数学-解析版 附详细解题过程

④ YMO世界青少年奥林匹克数学竞赛-解析版 附详细解题过程

⑦ 美国数学大联盟杯-解析版 附详细解题过程

⑧ 鹏程杯-解析版 附详细解题过程

①《人大附中早培海选必刷》《八中海选训练与解析》电子版教材

② 八少八素、人大附早培神测千题（上 下册）

③ 人大附、八中海选神测万题练习册及答案解析.pdf

④ 八少八素试题分享&人大附早培班试题分享+神测复习资料

② 朗思 iESOL 备考资料

北京高中： 

① 北京高考英语听力机考模拟试卷及答案、听力原文、音频

添加 家长论坛微信