网传华数之星就是曾经鼎鼎大名的华杯赛，但事实上，教育部官方认可的数学竞赛中并没有华数之星。

根据教育部《关于公布2021—2022学年面向中小学生的全国性竞赛活动的通知》精神，从2021年9月到2022年8月全国仅有20项自然科学素养类竞赛是针对中小学生的，其中数学竞赛只有一项，叫全国中学生数学奥林匹克竞赛，这项竞赛是面向高中生的，目前已经没有面向小学和初中生的数学竞赛。

显然，华数之星并没有得到教育部的官方认可。但是，今天报名华数之星的人很多，以至于网络都卡到像春运时的12306网站，很多人用了10多分钟才登录进去。

我猜报名的大部分人都是想着能对小升初有帮助。现在许多城市的小升初已经实行全摇号了，但还有部分城市存在小升初点招的现象，华数之星的奖牌对点招有多大作用，属于仁者见仁智者见智了。 

我的观点是：如果奔着升学参加“华数之星”竞赛，那可能会大失所望。原因很简单，教育部2022年的工作要点中提出：全面落实免试就近入学全覆盖和公民同招，指导各地完善学校划片政策。“全面落实”这4个字，肯定不会是一句空话。

虽然对小升初来说，数学竞赛作用很小。但对于上大学、上名校来说，通过竞赛路线上名牌大学的路仍然很宽阔，主要有保送、特殊类型招生和强基计划等几大类，双减之后，这几条路并没有断，名校甚至更喜欢竞赛获奖的学生。

我以前曾专门写文章阐述过竞赛路线是什么，该怎么走，有什么用的问题，感兴趣的朋友请参阅文章末尾相关链接的最后一条。

竞赛必须从娃娃抓起，小奥和高联之间联系非常紧密，小奥中的数论和组合可以直接过渡到高联。从这个意义上来说，学习小奥并参加相关竞赛大有益处。

一方面，参加竞赛是对学习成果的检验，有利于查缺补漏；另一方面，参加竞赛能够帮助孩子找准自己的定位，知道自己在全国竞赛生中的大概排名。就目前的情况而言，小奥获奖不一定能在高联获奖，但小奥如果都学不明白，就说明完全不适合走竞赛路线。

但是，今年的华数之星比赛起不到这个效果，最大的原因是题目太过简单，比前几年的简单多了，甚至比不过前段时间刚结束的希望杯。考完之后，某家长群里的交流充分说明了这点：

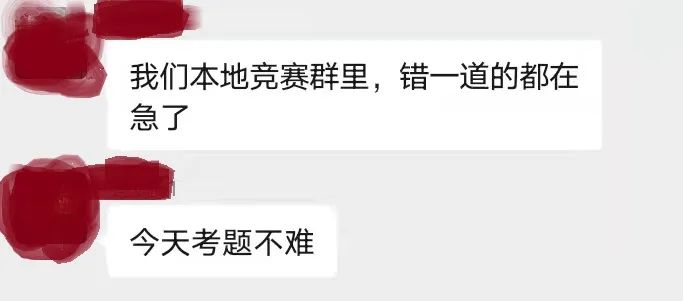
更让人大跌眼镜的是，有人发现题目居然不是新出的：

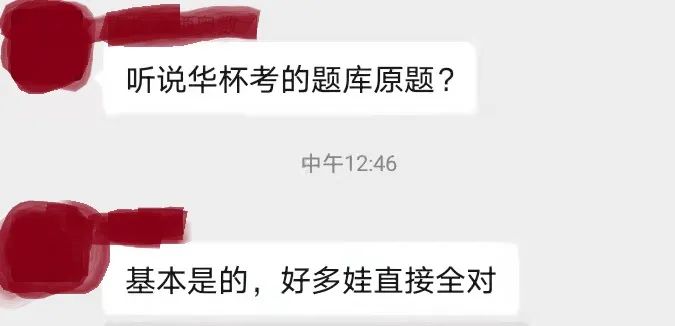
这样一个受众多家长关注的竞赛，居然出现这种问题，只能说明竞赛的组织者是在糊弄人，难道就是为了那几百块钱的报名费？

我只想对“华数之星”的组织者说一句话：想挣钱可以理解，但请先把事情干好，不能为了挣钱糊弄这么多家长。

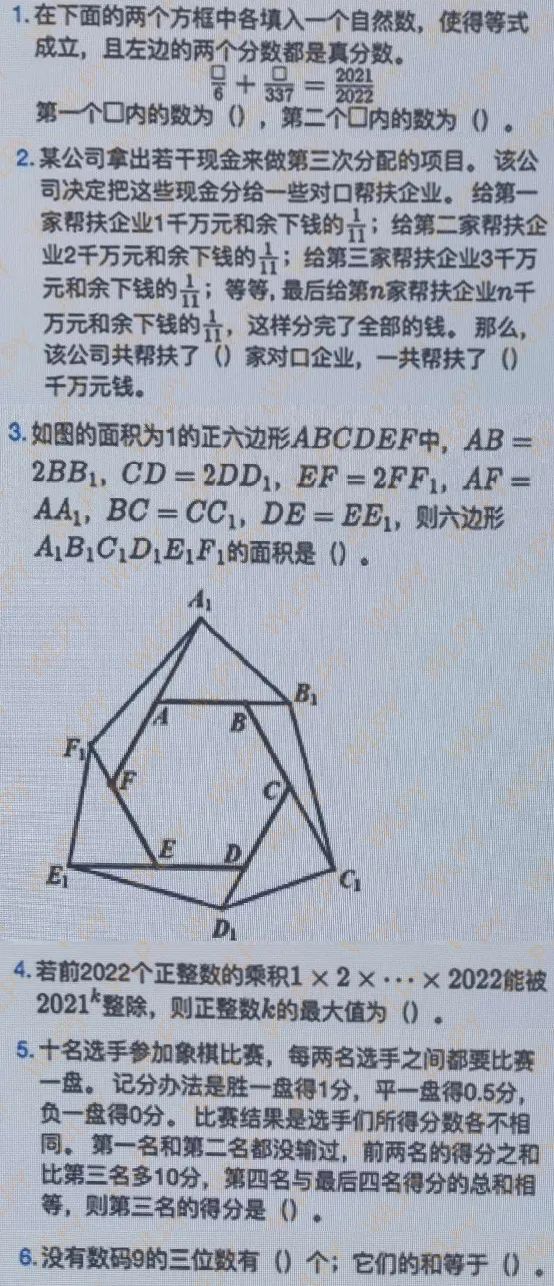
下面就是“华数之星”竞赛的小学高年级组题目，感兴趣的朋友可以自己做做，欢迎把答案写在评论区。

都看到这里了，点个赞再走吧。下面进入数学时间，先给出昨天思考题的一种解题思路。虽然在留言区“雨京”等已经给出了正确解答，我还是写一下用小学数论就能看懂的方法。

思考题（4星半难度）：

小明想找到一个自然数n，使5ⁿ中含有2022个连续相同的数字。请问小明的想法能实现吗？

解题思路：

首先一定存在一个自然数m，使2^m>10²⁰²²。

由于2和5的最大公约数是1，故存在某个正整数k,使5^k除以2^m的余数是1。

则5^k+m除以2^m的余数与5^m除以2^m的余数相同。

显然，5^m<10^m=5^m2^m<5^k+m,

假设5^m是b位数，则5^k+m从右到左数的话，第b+1,b+2,…，m位数都是0，

又因为此时5^m=10^m/2^m<10^m-2022,

则5^k+m中至少有2022个0。

所以小明的想法能实现。

下面再给出一道组合题，解题所用知识不超过初中一年级。题目只针对竞赛生，不打算参加竞赛的学生请忽略本题。

思考题（4星半难度）：

握手这个事是相互的。某次会议上共有34个人参加，结果发现任意4个人中，均有一个人与其余3人都握过手。小明说：至少有31个人，他们每一个都和参会的所有人都握过手。请问小明的说法正确吗？