今天给大家推送2022韩国数学奥林匹克决赛试题。以下内容来自于微信公众号：久霖竞赛田。

第一天

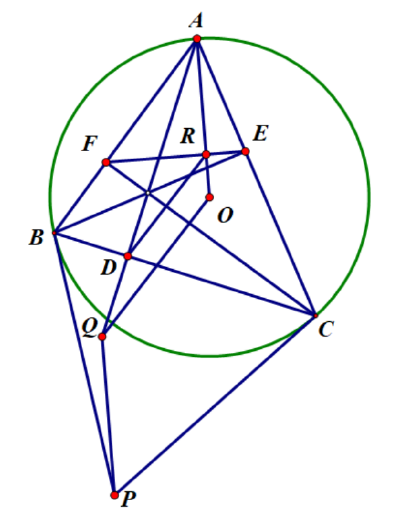
1.锐角外心为, 三条高分别为. 过分别作的切线, 两者交于点. 过作垂线与交于点. 过作于. 求证: 互相平行.

2.有个盒子  , 每个盒子中有非负个数的石子(即可以没有). 所有盒中共有个石子. 接下来, 进行如下操作:
在每一步中, 选择一个盒子, 将盒中的石子划分为个部分, 使得其中任意两个部分的石头个数的差不超过, 随后, 将这个部分逐个放入个盒子中.
一直操作, 直到只有一个盒子有石子, 其他盒子中石子个数均为为止. 此时, 设为对盒中石子个数为的盒子完成操作所需的最小步数. 求的最大值, 并求最大时, 的所有可能值.

3.给定函数, 已知它的值域为有限集. 求所有函数, 使得对任意实数, 均有

第二天

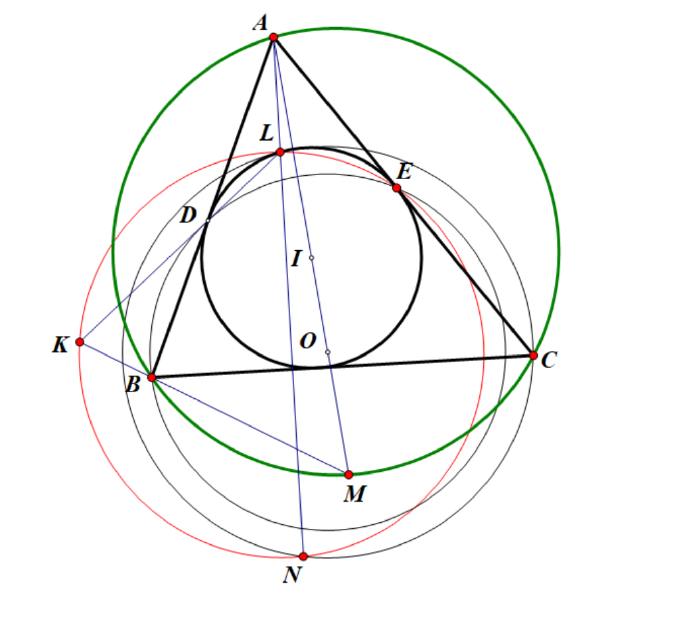
4.非等腰内心为, 与其外接圆再次交于点. 其内切圆与分别切于点. 设为外心, 过作的垂线与交于, 且在同侧. 以为圆心,为半径作圆, 直线与再次交于点. 直线交于点. 求证: 共圆.

5.求所有正整数, 使得存在整数, 满足

6.若集和满足如下条件, 就称它是"梦幻"的:
.
中所有元素都是闭区间的子集.
对任意实数中包含的元素个数不超过.
对梦幻的集合,  设表示满足以及, 的区间对的个数. 求的最大值.