全球规模校际数学思维挑战活动——澳大利亚数学思维挑战(AMC)


AMC
澳大利亚数学思维挑战活动
全球超大规模的校际数学思维挑战活动
44 年历史,总计32 个国家
1600 万名学生参与
国际权威学术机构
澳大利亚数学联合会 (AMT) 举办
5 个难度级别
适合各个年级学生参与
官方提供中英文试卷,方便中国学生参与
约60% 获奖率
你是否看过以下2幅作品?
你是否知道其中还蕴含着数学原理?

图片来源于网络《蒙娜丽莎》

图片来源于网络《最后的晚餐》
答案揭晓
这两幅画都满足了同样一个数学数列-斐波那契数列,即同样满足黄金螺旋。
斐波那契数列到底是什么呢?
斐波那契数列由十三世纪意大利数学家斐波那契发现。数列中的一系列数字常被人们称之为神奇数奇异数。具体数列为:1,1,2,3,5,8,13,21,34,55,89,144,233等等,这个数列从第三个数字开始(第三个数字是“1”),每个数字都是前两个数字之和。由于此数列是以研究兔子繁殖为例研究的数列,故又称为“兔子数列”。
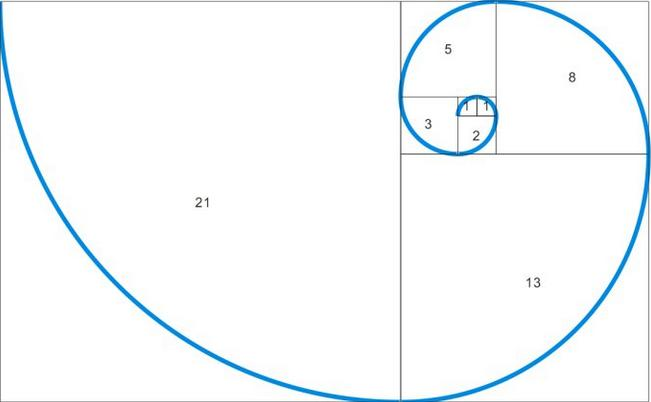
而斐波那契螺旋线,也被称为“黄金螺旋”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个90度的扇形,连起来的弧线就是斐波那契螺旋线。

自然界中,有很多满足斐波拉契数列的现象。例如,树木的生长,由于新生的枝条,往往需要一段“休息”时间,供自身生长,而后才能萌发新枝。所以,一株树苗在一段间隔,例如一年,以后长出一条新枝;第二年新枝“休息”,老枝依旧萌发;此后,老枝与“休息”过一年的枝同时萌发,当年生的新枝则次年“休息”。这样,一株树木各个年份的枝桠数,便构成斐波那契数列。
另外,观察松果、凤梨、树叶、某些花朵的花瓣数(典型的有向日葵花瓣)某些花朵的花瓣数(典型的有向日葵花瓣),蜂巢,蜻蜓翅膀等,可以发现它们都具有斐波那契数:3、5、8、13、21……
这些生物懂得斐波那契数列吗?应该并非如此,它们只是按照自然的规律才进化成这样。这似乎是生物生存的“优化方式”,它能使所有生物自身生长成为最适应生存的完美状态。

欧洲文艺复兴时期,黄金分割广泛运用于美学中,绘画、雕塑、建筑都有黄金分割的身影,因此,维纳斯的雕像、达芬奇的绘画都具有黄金分割的应用。到今天,黄金分割的应用已经不是纯数学问题,它不仅仅广泛运用于美术、建筑、设计等美学领域,还被广泛应用到生物学、音乐、物理学、经济学、心理学和预测学,甚至政治和文化,几乎遍及各个领域,对人类影响深远。
数学是充满魅力和无限可能性的,
数学是鲜活的,不是冰冷的,
它存在于生活的方方面面,与我们的生活息息相关。
想要体验初阶数学的乐趣吗?
快来参与全球极具影响力的
美国数学思维挑战活动(AMC)

② 知名机构人大附早早培(zzp)学前集训队-数学/神测和动手
① 华杯赛/华数之星真题试卷-解析版 附详细解题过程
② 迎春杯/青少年创新能力测试-解析版 附详细解题过程
③ 希望杯/希望数学-解析版 附详细解题过程
④ YMO世界青少年奥林匹克数学竞赛-解析版 附详细解题过程
⑦ 美国数学大联盟杯-解析版 附详细解题过程
⑧ 鹏程杯-解析版 附详细解题过程
①《人大附中早培海选必刷》《八中海选训练与解析》电子版教材
② 八少八素、人大附早培神测千题(上 下册)
③ 人大附、八中海选神测万题练习册及答案解析.pdf
④ 八少八素试题分享&人大附早培班试题分享+神测复习资料
② 朗思 iESOL 备考资料
北京高中:
① 北京高考英语听力机考模拟试卷及答案、听力原文、音频
添加 家长论坛微信



全部 0条评论