距离中考还剩一个月时间了，为了让初三的同学们更高效的准备中考，我对南京市近三年的中考数学做个全面的分析，并且根据卷子的特点提几点复习的重点，希望对初三的学生有所帮助。

1.近三年中考知识点结构分析

我整理了南京中考近三年的考点，然后将每个知识点对应的年级（课本位置）进行了如下图分析：

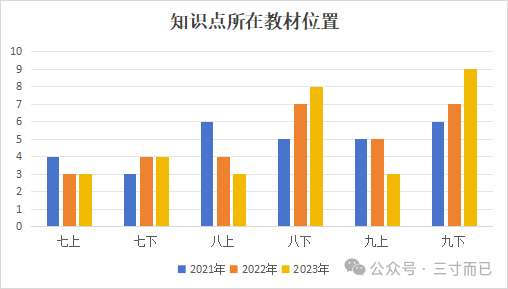
从上图看出：

（1）每年的中考对七年级（七上、七下）内容的考察基本上是一致的，根据知识点的结构，年级越低，知识点肯定是越单一，越简单的。换句话说，近三年每年中考的送分题是恒定的。

（2）相比较21年中考，22年和23年更加侧重考了八（下）和九年级的知识点，23年中考九（下）的占比是最大的。虽然这并不能说明卷子的难度越来越大了，但高年级的知识点越多，反映出卷子越来越综合了，中等以及中等偏上难度的题目增多了，这对中等偏上（108以下）的同学是致命的。举个例子：对于一个105左右，面对三份试卷，相比较21年中考，22年、23年的卷子更费时间和精力，这很有可能做到最后时间不够或者状态变差，导致分数不理想。所以说这两年越来越多的学生考出来之后叫苦连天，觉得数学卷子有点难。

2.知识点出现频率分析
每年的中考总是会出现以往的一些固定知识点，当然也会出现一些新的题型，接下来我们以23年为例去看看每个知识点出现的频数。

2023年南京中考知识点
知识点	对应题号	出现次数
幂的运算	11	3
科学记数法	1	3
分式的化简	17	3
一元一次不等式组/整数解	18	3
概率	21	3
扇形/条形/折线统计图	20	3
尺规作图/作图	24、27	3
二次根式的运算	9	3
二次函数的图像与性质	25	3
三角函数的应用	23	3
一次函数的实际应用	13	3
勾股定理的应用	5	3
三大变换-旋转相似	27	3
估算无理数的大小	2	2
圆与正多边形	15	2
反比例函数k的几何意义	14	2
分式有意义	8	2
数据的分析-中位数	12	2
平行四边形	19、27	2
相似综合	16、24、26、27	2
三角形的三边关系	3	2
代几综合 （用函数解决几何问题）	26	2
圆与相似	26	1
四边形的翻折	16	1
因式分解	10	1
一元一次方程的应用	22	1
圆与相似（最值）	24	1
有理数的计算（绝对值）	7	1
平方根和算数平方根	7	1
反比例函数的应用	4	1
相似三角形的常见模型 （三平行模型）	6	1

统计如下：

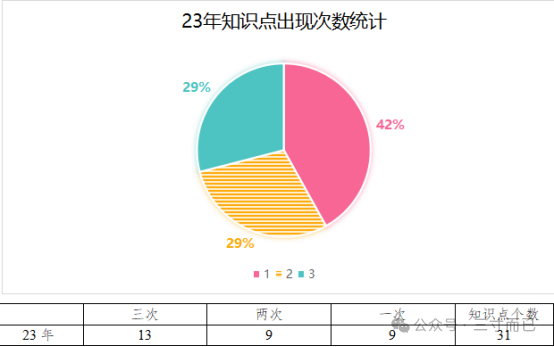
以上统计中，近三分之一的知识点是近三年连续考到的，对应的分值大概在70分左右。统计表中出现一次的标黄知识点是比较基础的，同时也是近五年中考中考到的。只要最后两个知识点题型是首次考到的。
鉴于以上分析，我觉得二模过后，大部分同学主要的精力都应该放在近五年的中考卷上，先认真刷每一份中考卷，刷完之后整理中考错题，找老师问明白，然后再打印出来，重新做一遍。不建议自己看答案，凭记忆做一遍错题。而是要清楚和理解背后的考点和逻辑。前面的都完成之后，最好再拿张白纸，自己总结一下五张卷子上所有的考点，下图是我以前让初三的学生做的，大家可以参考：

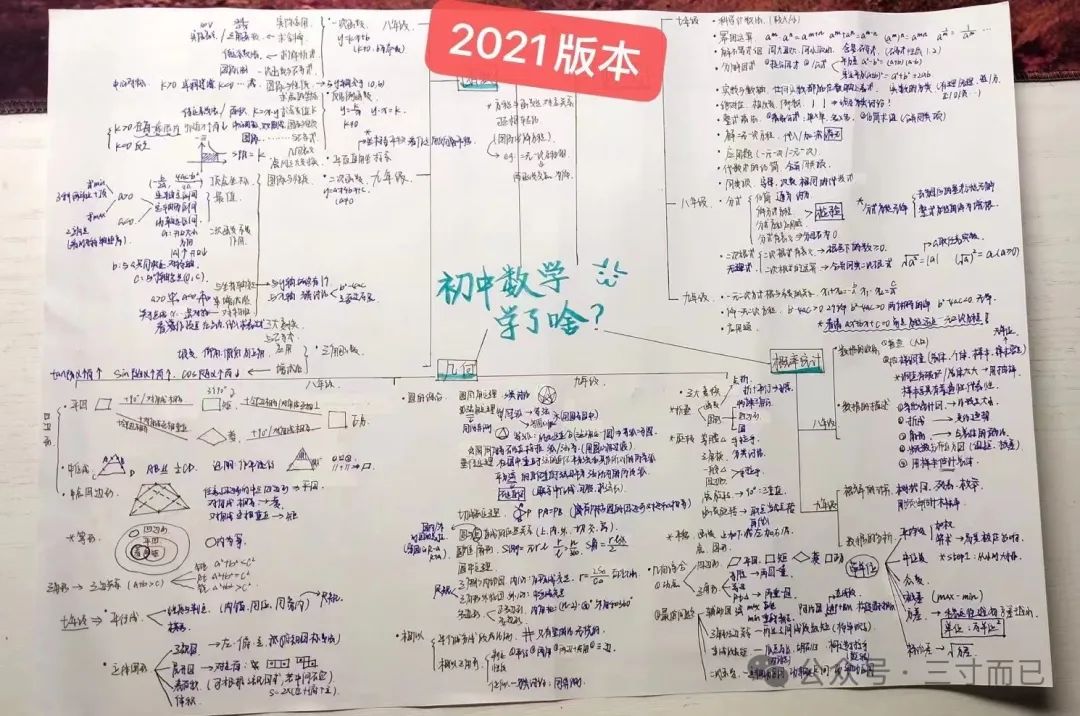
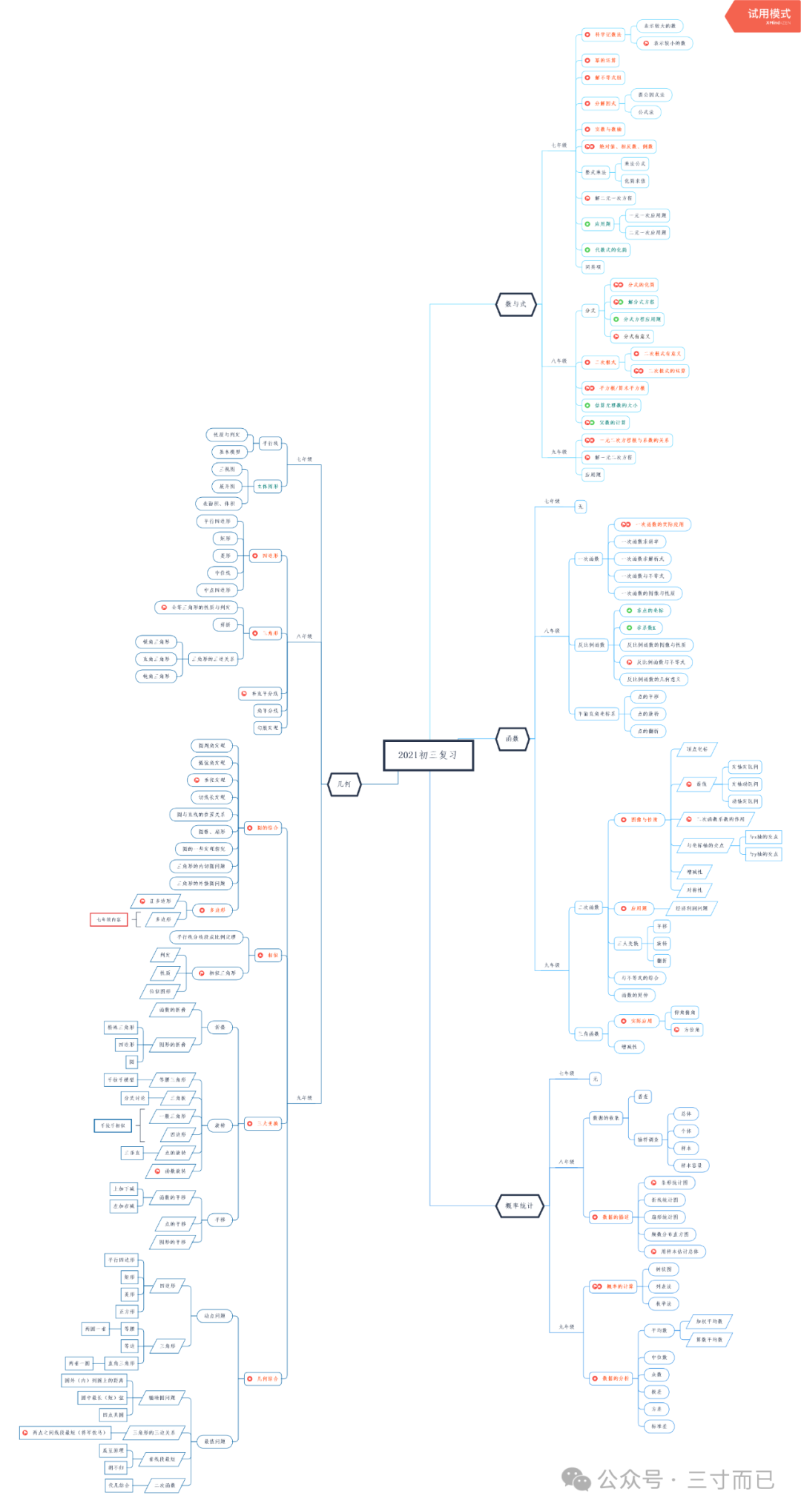
3.重点题型说明：

（1）关于压轴题

南京中考的压轴题（27题）21年前后有明显的变化，这也是22年新课标改革后的呈现。19年到21年主要是数学建模解决实际生活问题为主，最后一问偏向于开放化，提供解决问题的思路即可；21年之后连续两年都是几何旋转+相似，重点考察了学生的几何理解、推理、想象、操作等能力。

22年、23年整体的命题思路都是新定义（考察学生抽象理解能力）、通过变换的语言描述，完成尺规作图（概念理解/操作能力）、证明（推理能力），求解一系列的问题。

（2）关于代几综合（用函数解决几何问题）

22年、23年的中考还有个很大的变化是关于代几综合的考察，但不同于其它市，题目都是通过函数解决几何问题。比如22年的T26，23年的T26，这就要求学生用变化的眼光看待图形，重视图形中点、线段等各要素之间的联系，甚至是局部和整体的联系，能让学生更加直观的了解图形辅助线的形成，使得学生的推理能力更上一层楼。其实大多数同学都惧怕动点，一见到动点就犯怵，这也是这两年中考的高分段学生没有以前多的原因。但这种题型是以后的常态还是这两年特例还有待今年中考的验证。

（3）关于准备压轴题的一点建议：
①重视几何的基础，特别是相似的运用能力；

②重视计算能力，特别是涉及到一些带参代数式的化简和计算，我见过很多人思路没问题，但牵扯到代数式的推导，很多人就放弃了；

③重视作图能力，特别是常规作图的熟练度，比如通过相似构造线段的长度（射影定理）；

④放平心态，理性对待，懂得放弃。数学的压轴题很考察学生的理解能力，别想着通过大量的刷题就能解决。最后的两三分决定不了你的人生，适当的留时间检查一下前面的题，检查出来一道错误和做出来压轴题，效果上是一样的，但明显检查更容易。