1

某国家有 11 个飞机场，各个飞机场两两之间都有航线，为节约资源，想减少一些航线，同时满足：①对任意两个机场，要么可以直达，要么可以通过另一个机场转机一次到达；②不允许存在 3 个机场两两之间有直达航线，则最多可以减少____条航线，最少可以减少___条航线

解析：

十一个机场，任选2个机场，所有可能性为C（11，2）=11×10÷（2×1）=55（条）；要求减少最多，剩下的航班最少，由①，任意两个机场可以转机到达，电线图必然时连通的，11个机场至少10个机场相连，减少55-10=45(条）构造如下图：

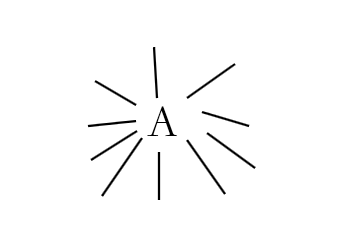
要求减少最少，剩下航班尽量多，不妨找到最特殊的，拥有航线最多的机场A，设A有K个机场，分别是M,N,P....，

由于不允许有3个机场两两有直达航线，则这k个机场之间没有任何航线，航线是有剩余（11-k）个机场产生，每个机场航线不超过最多的路线K条，则所有航线最多(11-k)k条，和一定，差小积大，所以当k=5或6时，最多路线5×6=30（条），减少55-30=25（条），总分两组，组内不连，组间相连构造如图

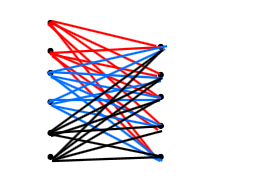
评析：通过①减弱使用，考察了图论中经典的连通图；②则是考察完全二部图（我们把总分两组，组内完成不连，组间全部相连的图称为二部图，比如本图即K56）

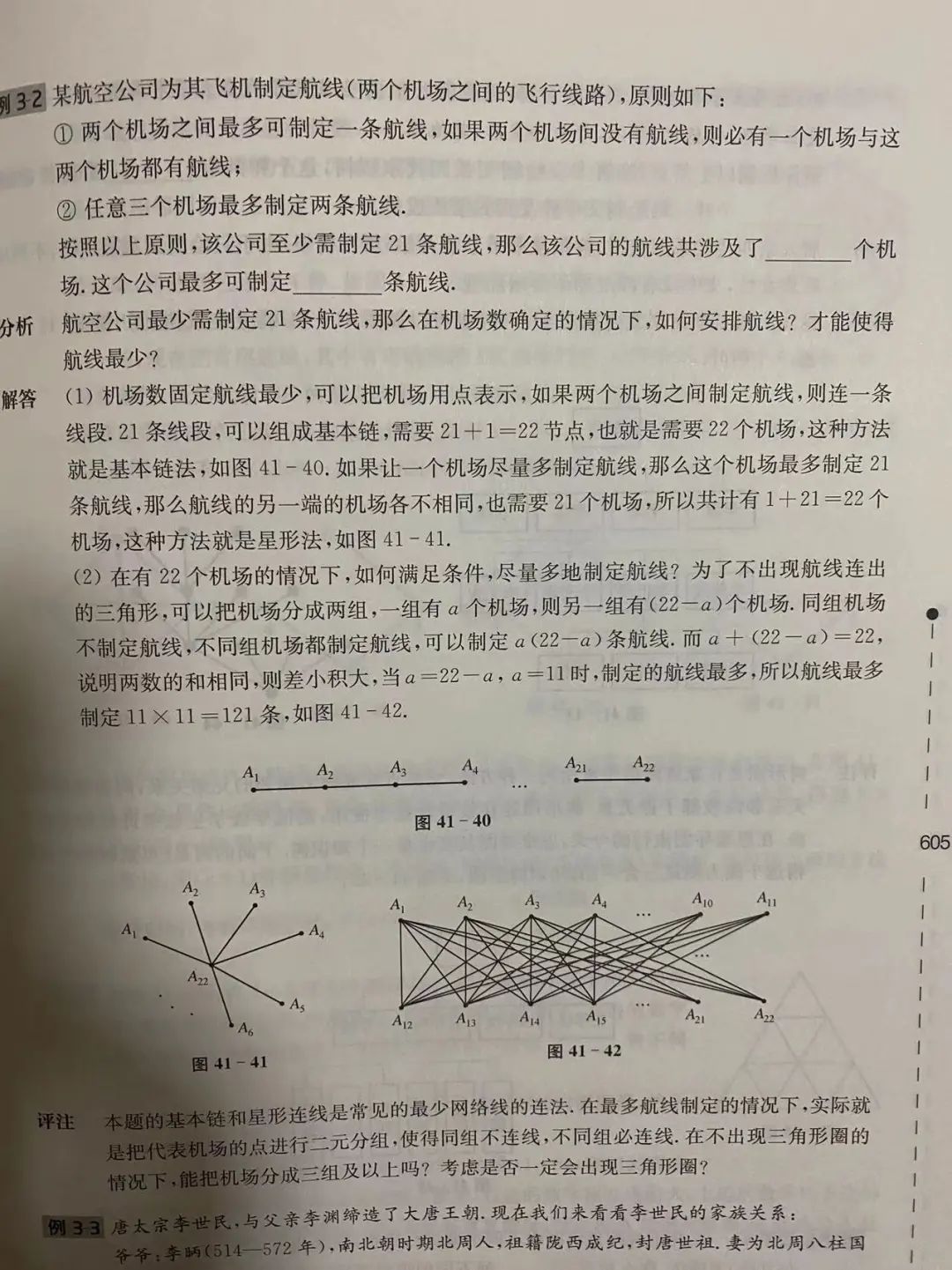
本题也是有成题的，在《小学奥数教练员手册》605页，小杰看到了非常类似的问题，首先数据结构变得更稍微简单一些，其次还是逆向思考，由最多航线求得飞机场数量，然后再求最多飞机场数量，典型的反问题。由加变减，由果索因。

2

某国家有若干城市，他们的航线满足：对任意三个城市，都至少有一条航线连接其中两个；对任意四个城市，一定存在两个城市之间没有航线连接，则城市的最大值为______

解析：

任选一个城市A，则和A有航线的城市最多不超过5个。

若存在6个城市有航线，那么任意6个城市，必有3个城市互有航线或3个城市互相没有航线（拉姆塞原理），加上城市A，必然存在3个城市互有航线，或者4个城市互相没有航线，与题目矛盾，故A至多和5个城市有航线。

A没有航线的城市不超过3个

若存在4个城市与A没有航线，根据三个城市至少有一条航线，则这四个城市必两两有航线，这与 任意4个城市至少有两个城市没有航线矛盾，故A最多与3个城市没有航线。

综合，最少有1+3+5=9（个）城市，但是如果真的构造9个城市，那么每一个城市都需要和5个城市通航，通航总次数是5×9=45（次），通航总次数肯定是偶数次，45次与握手定理矛盾。不存在9个城市的情况。

那么最少是8个城市，构造如下：

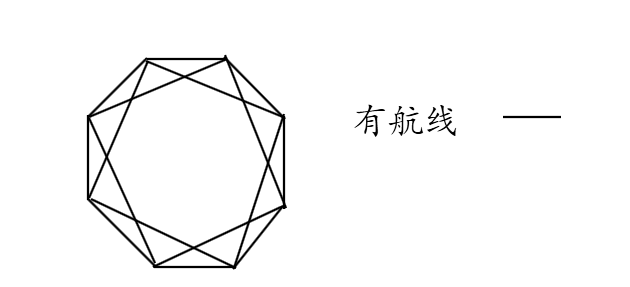
评析：

本题其实是高联的一道成题，在《奥赛经典》里面有收录，换了个场景。

《世界奥林匹克大辞典》也收录过很多相关的题目

当然，其实这道题本质上是拉姆塞原理在9个人时候结论的逆运用，即便我们讲到拉姆塞原理，也很少逆向思维，比如我们知道任意6个人必然有三个人相识或者三个人不相识，那么反过来最多5个人可以保证任意三人都不能两两认识，或者两两不认识。

下面就是本题的反面证明：

3

第3道：

某城市有15个旅游景点，两两之间有直达道路连接，则一共有___条路。这些道路中，有15条是主干道，可以双向通行，其余是单行道，只能从一个景点通往另一个，如果3个景点满足：从其中任意一个出发，通过三个景点之间的道路可以到达另外两个，则称三个景点为“互通三景点，”那么15个旅游景点中，“互通三景点”最多有___组。

解析：

一共有C(15,2)=105(条）；

单行道：105-·5=90（条）；“互通三景点最多”，总共的“三景点”C(15,3)=455(条），则“不互通三景点”最少，不互通如图

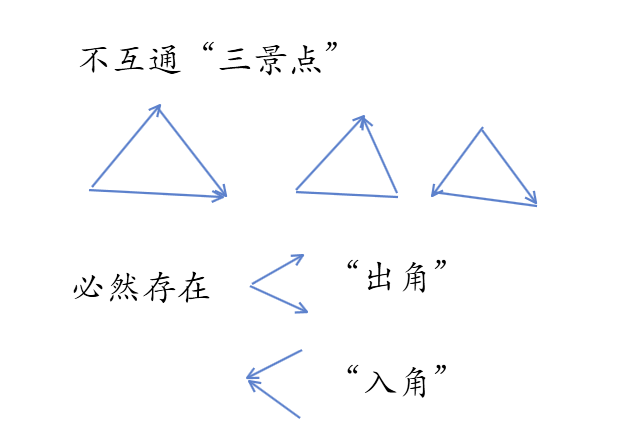
如图所示，不互通三角形必然有“入角”或“出角”，不互通三角形尽量少，那么不互通的三角形，尽量多“消耗”入角和出角，尽量不使用主干道

先分析“出角”，由两条“出线”产生，不妨假设15个点分别有a1,a2,a3....a15条出线，

则有a1+a2+a3+....+a15=90，

出角的个数=C(a1,2)+C(a2,2)+C(a3,2)+...+C(a15,2)

=a1(a1-1)+a2(a2-1)+...+a15(a15-1)

=(a1²+a2²+...+a15²)/2-(a1+a2+...+a15)/2

a1+a2+...+a15)/2=45

求(a1²+a2²+...+a15²)/2=（6²+6²+...6²）/2=270

270-45=225（个），则同理入角也是最少225个

每个不互通三角形最多消耗2个同向角，最多450÷2=225（个）

构造每个点6出6入，不互通三角形无主干道

15个点，相邻点连接主干道，从第1点开始，依次出、入、出、入交替连接其余点

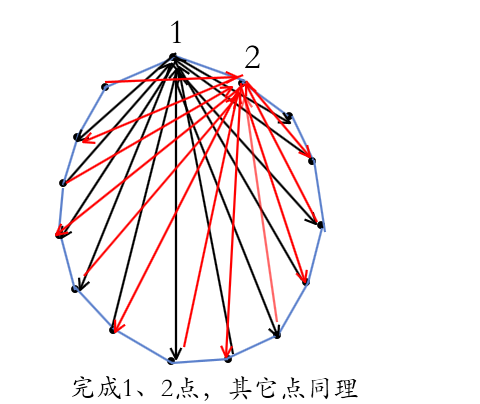
评析：论证和构造都非常复杂，最值原理和极端思想的考察。

小杰做也翻车了。写解析就是这样，做多错多，费最多的力，最不讨好，虽然一时便利家长，但是不带来任何收益，做错了还会被说“误人子弟”。

一些想法

1、对学生

从上面道题我们可以看出，早培初筛特别喜欢有扎实的基础功底，良好的理解能力，能够灵活运用知识，懂得思考问题的孩子。以前考试考察“神测”，主要是出题方便，线下多次考试的过程中，出神测先考的学生优势不大，但是如果还是像2021这样，初试在网络上同时进行，那么类似的知识想考察什么都可以。

只要懂得理解、应用、转化，考察底层的逻辑能力，思考能力，学习能力，分析判断能力，要在“直觉-判断-辩论-观点”的逻辑下，理解题目含义，形成自己对于某个知识的观点和看法。在我们学习的时候，一定要多问自己：这个问题可以变化吗？可以有多解吗？可以知道结果如果反推过程？有没有和更加高级的知识有联系？

勤学多问为什么。

更加直白的说，早培孩子的选拔更接近高考标准，需要对知识的理解，应用、转化。单纯的知道、了解某个知识，细心，避免犯错，能达到基础标准，但不是早培要选拔的孩子。

2、对老师

准备早培，也就是必须要准备一些基础知识，在准备初期会提升很快，符合这样的知识有很多，大多在组合版块，比如：概率与期望，图论与交通，人际关系与社会活动，比赛与考试，最值问题，操作类问题，染色问题。数论版块也可以出这类问题，比如费马小定理，n进制，完全平方数，取整，数字和问题（但是由于小奥在这一块已经非常成熟，如果要考察肯定是在数论中找一些更边角的地方考察）

大部分老师都能培训，但是很快会达到瓶颈，后续非常难以跟上，甚至过多的培训反而会起相反的效果。

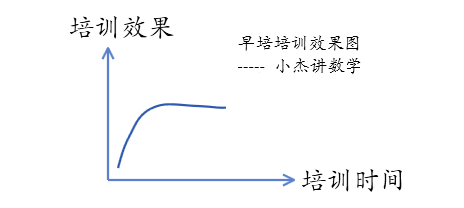
就这几道题有很多高中竞赛痕迹，有的甚至就是高中竞赛原题，出题人像是经过系统训练的高中竞赛教练，选出小学生能够理解的一部分竞赛知识，改编一些成题，完成命题。想要继续提升，需要孩子有天分和毅力，有系统的培训，有特别好的老师指导。打破瓶颈。

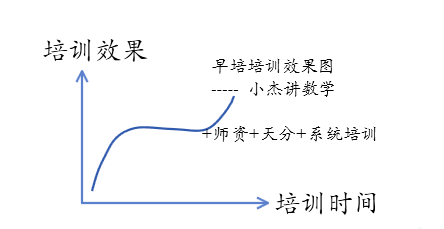
我理想的早培老师最好是北大数院或者中科大少年班毕业，有高中数学竞赛背景，并且带过机构集训队，有强命题能力，有5年以上教学经验的老师。