今年ZP入营阶段数学试题赏析

写在前面:
今年ZP其实早在一个星期之前就落下帷幕了。
然而彼时另一个重要活动还未举办,所以我的暑期一如既往地匆忙,根本没有时间更新公众号写些啥。
昨天终于目送孩子上了参加活动的大巴,却又在医院呆了整整一天,等背了几公斤的药回家的时候已经没有写字的力气了。
看了看圈子里我关注的许多公众号,资讯方面该说的都被他们说了,不过好像没有其他公众号发布过入营阶段的考核内容。
所以今天就写写这个吧。
严正声明:
文中所出现的试题全部来自网络,出处不明,也不清楚具体来自于什么活动,也不保证试题的准确性。获取渠道与笔者无关。笔者只是偶然看到了这么一些题,然后跟大家分享一下罢了。
今年ZP整体活动流程及政策复盘
这部分内容早已失去了时效性,其他公众号也已经说得很多了,所以咱们这里就简单用个时间轴带过去,更详细的内容,欢迎大家移步杨宇泽老师的“泽哥点评”以及尹杰老师的“小杰讲数学”两个公众号了解。
毕竟我是个懒人,只研究题目本身,笑。
今年的时间流程如下:
7.16~7.18日:开放线上报名。
7.21日:线上全真模拟
7.23日:第一次线上活动(即所谓“初筛”),据说人数15000+
初筛整体活动内容参见下图,点击可放大:

初筛的数学部分,之前写了一篇文章,大家可以参考。当然现在网上已经有更全的试题跟解析了,所以看看就行。
7.25日:第二次线上活动(即所谓“复筛”),据说人数3000+
复筛整体活动内容参见下图,点击可放大:


7.28日:全天举行线下活动(即所谓“入营”),据统计约600人
入营政策面上,今年有特殊变化,强调两点:
1、除ZZP在读学员外,其余四年级学员一律未获得入营资格。所以之后想要让孩子提前考ZP的,四年级的尝试可能都只能到复筛这一步为止。
2、入营时需持有户籍证明+学籍证明+学生卡。有户籍不在海淀的孩子被劝离。如果明年政策不变,且现户籍不在海淀,最迟需要明年5月前买房办手续。
入营考核的具体内容参见下图,点击可放大:

8.1日:发布录取通知
入营上午场数学:逻辑部分赏析
上午场的逻辑考察的比较有意思,跟小奥里常见的逻辑推理非常不同,更接近于高中学习“命题”时会接触到的一些逻辑问题与判断,以及公务员行测中会出现的逻辑信息问题。
由于这部分内容不太“数学”,孩子考完出来后也只能回忆个大概,所以这部分只放一个比较符合孩子描述的同类题,真实题目如何就很难分说了。
1、经典三段论逻辑
用两个前提推导出一个结论,判断结论的正确性。类似下面这道题:

2、逆命题、否命题与逆否命题
原命题为真,则逆否命题为真,逆与否不一定为真。标准的高中内容,类似下面这道题:

3、“或”“且”“非”的逻辑门运算
让孩子理解这三个逻辑连接词的逻辑,并且代入运算规则求得结果,类似下面这道题,但比这个难:
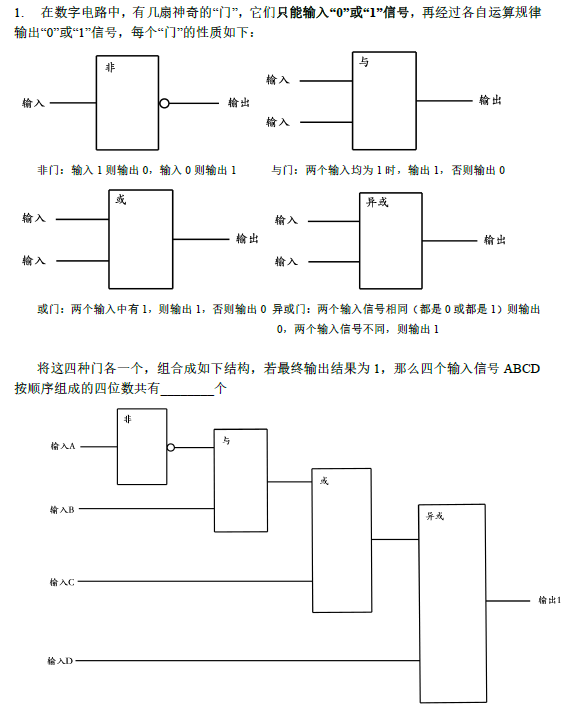
4、反证法的证明逻辑。
其实小学阶段对反证法的应用不算少,最典型如抽屉原理和染色论证中就大量充斥着反证法的思维。但很多孩子虽然能听懂,却很难自身严谨自洽的写出一个反证法的证明逻辑。
在这一部分,考了这样一道题,题目本身不算特别难,但让孩子写出严谨的证明逻辑,还是相当不容易的。
题目如下:
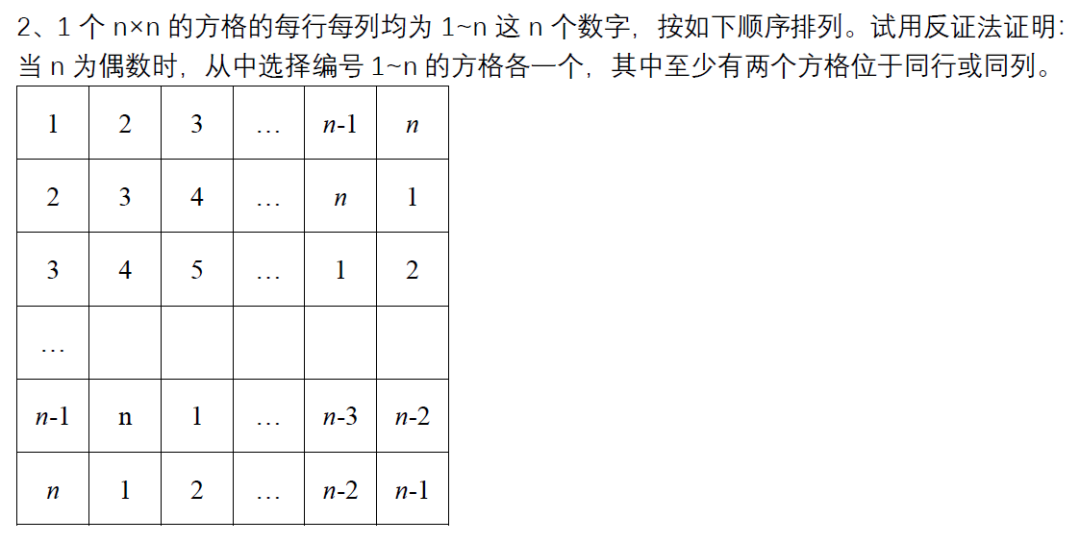
这道题题目提示了n为偶数,所以容易想到从奇偶性出发找矛盾。但最大的核心还是需要意识到,同一个数字所处的行列数之和永远是两种定值二选一。能够发现这一规律后,再利用反证法,借助总行列数之和找到矛盾即可。
参考解析如下:

入营下午场数学:必胜策略与博弈
去年入营有一场考试集中考察了概率这一专题,从古典概形、几何概率到条件概率都有涉及。
今年似乎继承了这一考察模式,考核内容为简单博弈论,或者用小奥传统的叫法,称为“必胜策略”。
小学阶段的必胜策略可以用两大逻辑概括所有问题的通解。
其一被称为“胜负点法”,将所有可能出现的情况按照“先手必胜”及“先手必败”分为两类。其中若某种情况下,先手玩家存在操作方式,让情景变为“先手必败点”留给对方,则这样的点是“先手必胜”点;反之,如果不管先手玩家怎么操作,都只能留给对方一个“先手必胜点”,这样的点就是“先手必败点”了。利用这样的递推关系,可以从最简单情况出发,推出所有情况的必胜和必败属性,决定必胜策略。
此类问题的经典模型是“巴什博弈”,即桌上有若干个小球,甲乙轮流取,每次可取数目有限制,问最后谁获胜。
本次入营五道题目中,足足有四道考察的是巴什博弈或其变形题,足见其重要性。
说句题外话,以我这么多年见过的机构老师来看,很多老师讲巴什博弈的讲法是完全的“偷懒式讲法”,甚至可以说是错误的讲法,不讲胜负点递推逻辑,只讲“凑总和”,孩子做题倒是快了,但难题就根本无从下手了。
希望这次早培的考察能引起一定的重视吧。
这部分试题中,比较有意思的是这样一个变形题:

因为每次操作完都还剩下两堆糖果,所以常规的必胜与必败点分析不太适用,但还是可以通过尝试,利用整体的奇偶性,定义一个新的递推规则,从而轻松解决问题。
参考解析如下:

我自己的暑期讲义上,刚好收录了比这道题再进阶一些的变形题,乃至ZP入营考完之后,有孩子开心的跟我说“老师你讲了个原题”。现在也把这道题放在这里供孩子们思考:

另一类策略则是“对称策略”。后手方只要能营造和先手完全对称的环境,就能保持不败最终必胜。
这类问题最典型的是尼姆博弈,即桌面上有n堆棋子,数目各自不同,每次轮流从同一堆中取棋子,个数不限的问题。
这里,ZP考察了一道和数论相关的对称策略问题,题目如下:

这道题说实话有点为难孩子了。题目本身不难,但是如何构造对称,特别是后半部分的对称,在考场上几乎无法给出一个合理的模型与证明。更遑论孩子的逻辑严密性远没有强大到可以写出这道题无可挑剔的过程来。即便是之前听机构老师讲过这道题的原题,要在考场上靠记忆和理解复现一个完美的过程,都绝非易事。
这里我站在一个孩子的角度,给出一个如果我像孩子们这么大的时候,靠自身能力可以勉强写出的过程:

这个过程看起来没有什么问题,感觉已经很“完美”了。你们能看出问题在哪吗?
下面是答案,反白处理了,大家可以思考过后再对答案。
【提示:用手机浏览时,长触屏幕再拖选,就能看到下面的反白内容】
甲的必胜策略基于对称性,41以上的对称非常容易满足,但1~40之间的数呢?甲如何保证“若乙写下1~40之间的一个数时,甲也写一个1~40之间的数”呢?或者说是否存在一种情况,让乙在写完1~40中的某个数之后,1~40之间恰好无数可写,从而甲被迫写下一个大于41的数,转胜为败?
当然,想要严谨的证明后半部分,证明和构造过程相对就很复杂了,留给小读者们思考吧。
整体来看,这次入营选拔的试题侧重逻辑和组合,选题大多经典而优美,从中也可以明显看出学校对于孩子数理逻辑能力的要求高于解题能力的要求,这也是数学的本来目的。
其他的题目因为本身不是特别全,篇幅也有限,就不放在这里了。

添加 家长论坛微信



全部 0条评论