2023-2024年AMC考试时间已出，可以备战了

: 梁老师北京小升初老师～

0 人点赞了该文章 · 64 浏览

距离2023年AMC10竞赛报名开始还有3个月，很多家长和同学们都在咨询有关报名和备考事宜。其中很多家长了解到AMC10竞赛分A/B卷后都十分好奇，AMC10竞赛的A/B卷有何不同？ AMC10竞赛A/B卷应该如何选择？AMC10竞赛A/B卷可以都报考吗？今天小编整理了AMC10的报考攻略，希望对各位有所帮助。

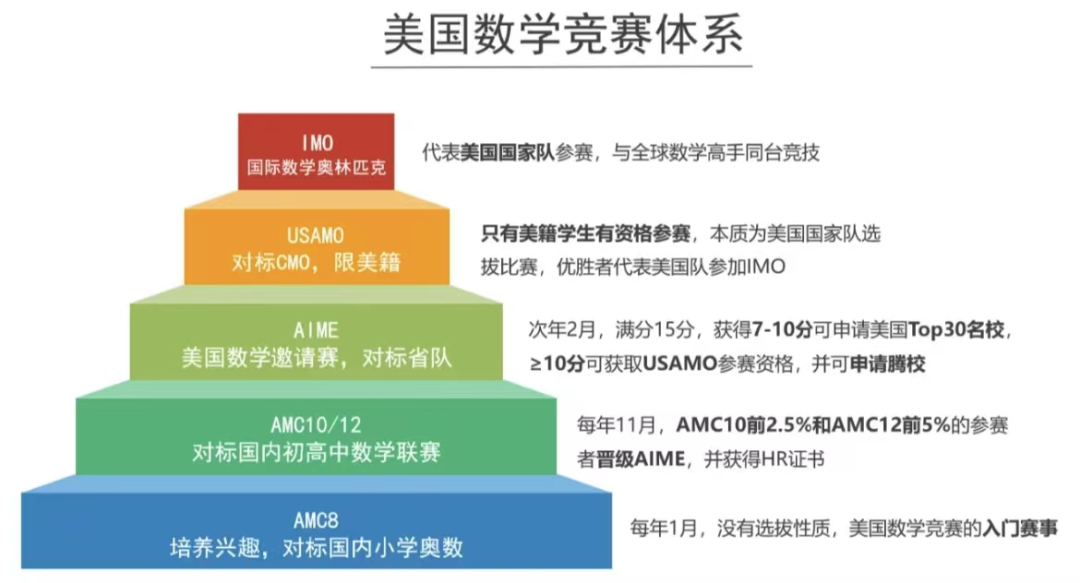
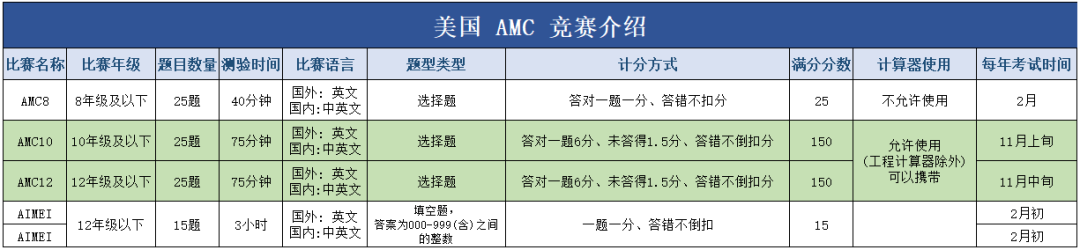
美国AMC数学竞赛介绍

美国AMC由美国数学协会MAA主办，目前每年全球超过6000所学校的30万名同学参赛，是全球非常有影响力的青少年数学竞赛之一。AMC的命题由美国AMC委员会全权负责，该委员会成员皆来自MIT、Harvard、Princeton等全美一流学府。

多年来，AMC还扮演为美国培育世界数学奥林匹克（IMO）选手的重大责任。AMC的研究人员通过AMC 8、AMC 10、AMC 12、AIME一系列测验，找出绩优生参加美国数学奥林匹克（USAMO），再从全美数十州筛选出24至30位精英，参加数学奥林匹克夏令营（MOSP）。再在夏令营中通过测试从其中选出六名队员参加IMO。

美国数学竞赛体制，经过层层赛事最后选出参加国际数学奥林匹克（IMO）的选手，晋级路径如下：

AMC10/12 美国数学竞赛
AIME 美国数学邀请赛
USAMO 美国数学奥林匹克
MOSP 数学奥林匹克夏令营暨IMO国家队集训
IMO 国际数学奥林匹克

⚠️：美国USAMO、IMO仅限美国公民和在美国或者加拿大读书的学生

AMC8/10/12是并列关系，学生没有参加AMC8考试，也可以去报名参赛AMC10/12。在AMC10和AMC12中取得好成绩可以晋级AIME的考试，最终综合AIME和AMC10/12的成绩，晋级者可以参加USJMO和USAMO这类更高等级考试。中国学生由于国籍限制，最终只能晋级到AIME阶段。

2023-2024 AMC考试时间

官方网址AMC中国区组委会
官方网址：
https://www.amc-china.com
ASDAN组委会官方网址：
https://www.seedasdan.org/

AMC8考试时间：2024年1月18-24日

AMC 10/12 A卷考试时间：2023年11月8日

AMC 10/12 B卷考试时间：2023年11月14日

AIME I考试时间：2024年2月1日 Invite Only

AIME II:考试时间：2024年2月7日 Invite Only

有家长问AMC10竞赛A/B卷可以一起报考吗？

可以！
AMC10和12每年会进行效力相同、难度相近的两次考试，即A卷和B卷。两份试卷除了考试时间不一样外，其他并无太大区别，大家根据自己的时间随意参加一即可，不必想太多。

注：以上时间为美东时间，与国内考试相差不远，确切时间以阿思丹公布为准！

AMC10/12 知识点

AMC10

进阶代数：多项式，余数定理，韦达定理，根与系数的关系，特殊高次方程；进阶不等式、均值不等式；函数入门，定义域和值域、二次函数、指数函数、对比函数、简单三角函数；数列进阶；代数技巧进阶。

进阶几何：进阶几何作图；三角形进阶、正弦定理、余弦定理、内切圆和外切圆，斯图瓦尔特定理，共点和共线；圆和四边形，四点共圆，圆的外切四边形；正多边形，角度，周长和面积；进阶平面几何技巧；解析几何入门。

立体几何：点、线、面的关系，三维坐标系；立体几何作图；正多面体，欧拉公式；特殊的立体几何图形，立体几何技巧。

进阶数论：数，数组和序列；模运算，复杂同余问题；整数、分数和小数，进制转换；进阶数论技巧。

进阶组合：容斥原理；二项式定理及相关结论；进阶排列、组合和概率；期望入门，递推、二分法，进阶组合方法。

AMC12

进阶代数：复杂不等式、调和不等式、轮换不等式、柯西不等式；复杂函数问题，反函数和符合函数，三角函数和差化积、积化和差，万能公式；复数，复平面，欧拉公式，蒂莫夫公式；数学归纳法、复杂数列和极限。

进阶几何：圆相关几何进阶；数形结合，二维、三维图形的函数表达，进阶解析几何；不规则二维、三维图形的处理；二维向量、三维向量。

进阶数论：二次余数，高次余数、费马圣诞节定理、费马小定理；各类丢番图方程的解法。

进阶组合：随机过程和期望；复杂组合问题技巧、基本综合问题。

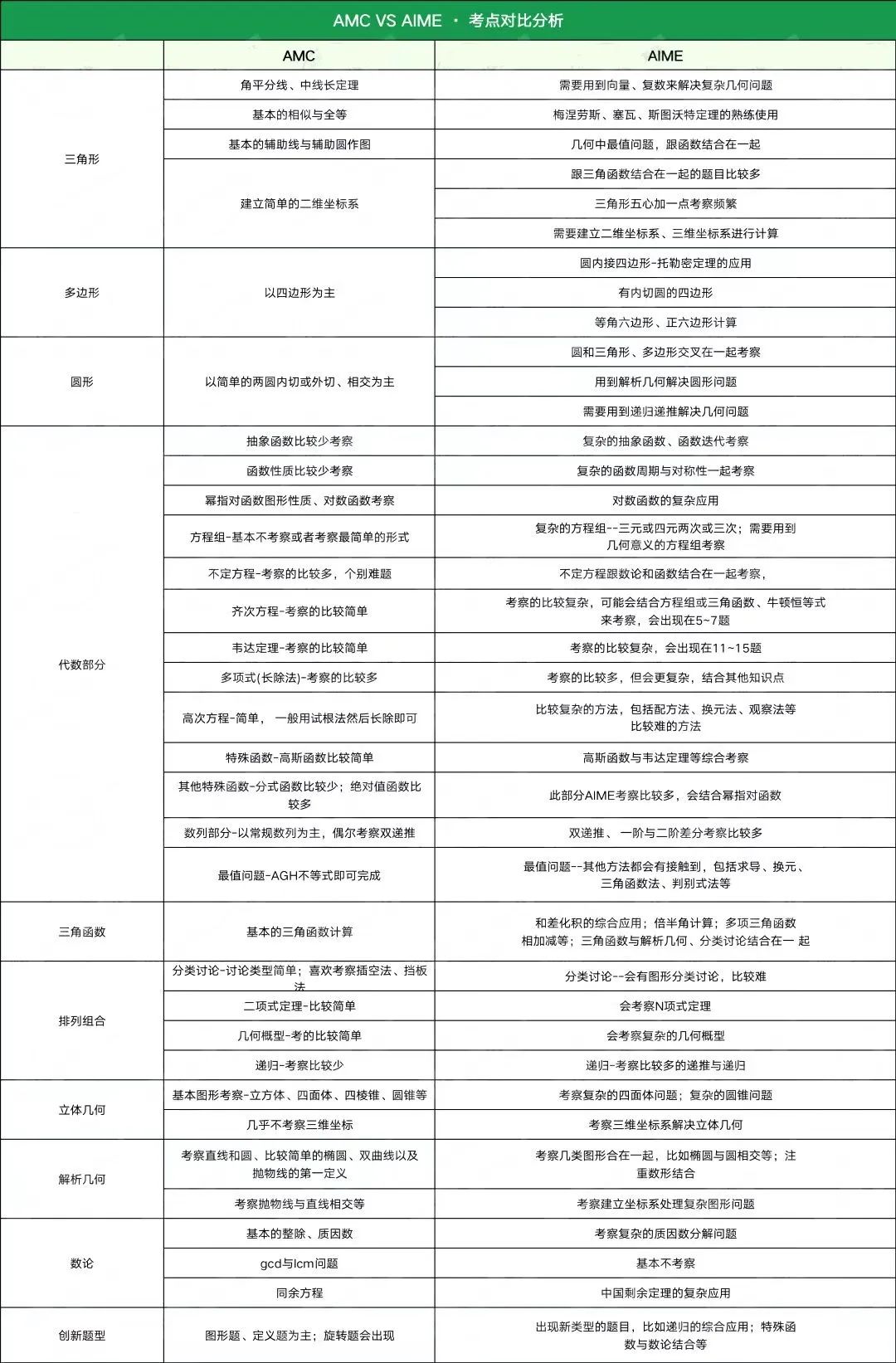
AMC与AIME知识点差别

AIME竞赛考试范围和AMC 10、AMC 12一样，考查范围仍然是算术、代数、计数、几何、数论和概率（微积分不在数学竞赛考查范围内），但允许使用微积分方法解题，但在这几大板块下，AIME会增加考点的深度和广度。

接下来，我们一起看看在相同考点下，AMC与AIME的考察侧重点的难度差异。

结合上表的考点分析，近年来的 AIME考试，AIME考试主要是集中在考察代数和几何部分内容，所以在晋级后可以着重准备这两个板块！

应该如何备考AMC

1
讲究策略，多刷真题
尽可能多刷历年AMC真题进行训练，根据往年晋级的学生统计，做5年以上的真题一般会有明显提升。基础一般的同学建议先练熟前15题，基础好的同学可以25题全面练习。

2
科学辅导，快速提高成绩
想在AMC竞赛中取得优异的成绩，不仅需要自己多刷真题自律学习，科学的课程辅导也是很有必要的哦！

添加家长论坛微信

2023-2024年AMC考试时间已出，可以备战了

梁老师北京小升初老师～

免责声明:

相关文章

2023-2024年AMC考试时间已出，可以备战了

梁老师 北京小升初老师～

免责声明:

相关文章

梁老师北京小升初老师～