一、选择题(每题5分，共50分)

❝

1、把一个正方体分割成8个大小相同的小正方体，小正方体的表面积之和比原来大正方体的表面积 增加了(     )倍。

A、1

B、2

C、3

D、4

❞

「答案解析」

每个小正方体新增了3个面，刚好是新增了1倍。

也可以假设原正方体变成为2，则其表面积为。

分割成8个小立方体后，总表面积为。

因此，增加了1倍。

选A。

❝

2、一件商品先涨价 15%，再降价 15%，该商品的价格(    )。

A、比原价低

B、比原价高

C、与原价相同

D、无法判断

❞

「答案解析」

最后定价是。

选A。

❝

3、分母是 2016 的所有最简真分数的和是(      )。

A、 288

B、 576

C、 144

D、 200

❞

「答案解析」

先分解质因数，由于。

根据欧拉函数，可以知道最简真分数的个数是：

对于这576个数中的任意一个分子为a的分数，必然存在一个对应的分子为2016-a的分数，这两个分数的和为1。

换句话说，如果a没法被2、3、7整除，则2016-a也一样没法被这三个数整除。

因此，选A。

当然，如果不能理解上面的思想，我们可以用集合的思想来死算。

所以，在分母为2016的所有真分数中，分子和为：

分子为2的倍数的和是：

分子为3的倍数的和是：

分子为7的倍数的和是：

分子为2x3的倍数的和是：

分子为2x7的倍数的和是：

分子为3x7的倍数的和是：

分子为2x3x7的倍数的和是：

所以，所有最简真分数的分子和就是：

因此，所有最简真分数的和为：

需要特别注意的是，死算的话其实用到的也是高中的集合知识，并且需要特别注意编者上面所用到的公因数1008的提取技巧，否则计算量很大。

选A。

❝

4、有盐水若干克，第一次加水若干，浓度变为 4%;然后又加入同样多的水，浓度变为3%;第三次再加入同样多的水，这时浓度变为(    )。

A、1%

B、2%

C、2.4%

D、2.8%

❞

「答案分析」

想不清楚就列方程。

譬如，设原有盐水x克，每次加水m克，则根据上述的关系，可以列出方程。

可以解得。

因此，第三次加水后的浓度就是：

选C。

❝

5.定义，读作N的阶乘。2019!能被7整除，如果把这个乘积去反复除以7，直到不能被7整除为止，从第一次除以7开始算，共可除以7 (  )次。

A、288

B、329

C、334

D、335

❞

「答案分析」

注意，除了7外，我们还要注意7的次幂。

次数就是：

选C。

❝

6.一个长方形的周长是 76 厘米，现将这个长方形的长和宽各增加 20 厘米变成一个新的长方形，新长方形的面积比原长方形的面积多(      )平方厘米。

A、400

B、760

C、1160

D、1520

❞

「答案分析」

这个题目可以用数形结合法来做，当然，设未知数也是可以的。

我们设长方形的长和宽分别为a和b，各增加20厘米后，增加的面积其实是两个长方形和一个正方形。

选C。

❝

7、有一个自然数，用它分别去除 62、90、130 都有余数，这三个余数的和是24。这三个余数中最大的是(    )。

A、14

B、16

C、18

D、19

❞

「答案分析」

根据题意，这个自然数肯定比62小，并且能被该自然数整除。

分解下质因数，

由于，余数和是24，那么，这个自然数肯定比8大。

因此，该自然数只能是43。

因此，最大的余数就是

选D。

❝

8、整数146 和234 的三个数位上数字的乘积都是24(注：，)，那么共有(    )个三位数其各位数字的乘积是 72。

A、24

B、25

C、26

D、27

❞

「答案分析」

分解下质因数，。

那么，可能的组合有

由于三个数的全排列共6种，有数重复则除以2。因此，这样的数共有

选A。

❝

9、己知一个质数的三倍与另一个质数的五倍的和是 301，则这两个质数的和是 (        )。

A、61

B、85

C、99

D、61或99

❞

「答案分析」

设这两质数是a和b，有：

根据奇偶性，必有一个质数为2，

假设a=2，则b=59。

假设b=2，则a=97。

因此，选D。

❝

10、如下图，梯形ABCD 的面积是120，AB=3CD,E为AC 的中点，BE 的延长线与 AD 交于 F，四边形CDFE的面积是(    )。

A、20

B、21

C、22

D、25

❞

「答案分析」

如下图所示，连接DE。

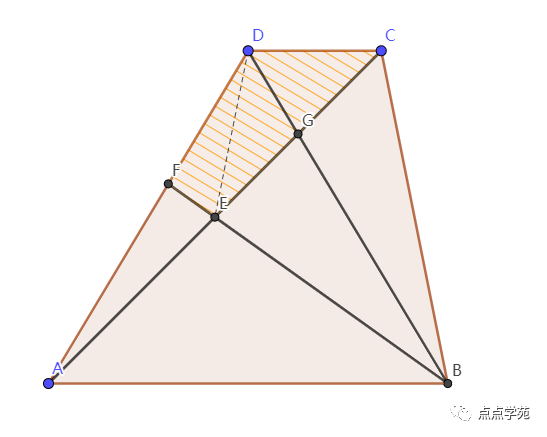
依题意，根据三角形的面积关系，可以知道：

，，

由于E是AC的中点，所以，

，。

根据蝴蝶原理，有：

，

,

。

所以，

。

所以，

。

所以，

，

所以，

。

所以，四边形CDFE的面积是平方厘米。

选B。

二、填空题(每题5分，共50分)

❝

1、（    ）

❞

「答案分析」

由于，所以，原式等于。

❝

2.已知质数 A、B、C 满足：，那么 的最大值是（    ）。

❞

「答案分析」

假设，那么，根据奇偶性，那么。

那么，要想积最大，那么B和C要接近45，

那么，很容易想到，。

因此，最大值就是。

❝

3、一项工程，甲、乙、丙三人合作需要15天完成。如果丙休息2天，乙就要多做4天，或者由甲、乙两人合作1天，这项工程由甲单独完成需要（    ）。

❞

「答案分析」

设方程来解答是很简单的，假设甲需要x天，乙需要y天，丙需要z天，则有：

很容易解得天。

从而可得天。

从而解得天。

❝

4、甲、乙二人练习跑步，若甲让乙先跑 20米，则甲跑10秒可追上乙;若乙比甲先跑3秒，则甲跑6 秒能追上乙,甲每秒跑（     ）米。

❞

「答案分析」

设方程来解答是很简单的，假设甲的速度是x，乙的速度是y，则有：

很容易解得，从而可得。

❝

5.一个三位数与 2019之和恰好是一个完全平方数，这样的三位数共有(      )个。

❞

「答案分析」

假设这个是x，那这样的三位数肯定比，比大。

由于，。

所以：

所以，这样的x可以从47排到54，一共8个。

❝

6.一辆汽车从甲地开往乙地，如果把车速提高 20%，可以比原定时间提前1小时到达；如果按原速度行驶 120 千米后，再将速度提高 25%，则可提前 40 分钟到达。那么甲、乙两地相距(     )千米。

❞

「答案分析」

提速20%后提前1小时到达，说明原来需要花费的时间是：

行驶过120千米后，时间没有节约，所节省的时间都是在提速25%后实现的。

假设甲乙相距为s，原有车速为v，则有：

由于，可以解得：

从而，，

从而可得千米。

❝

7、百货超市购进一批大米，第一个月售出大米的 40%，第二个月又售出大米 520 袋，这时已售出的 和剩下的数量比是5:1，则百货超市最初购进大米(   )袋。

❞

「答案分析」

设原购进大米x袋，

则有，从而可得袋。

❝

8、某次数学竞赛原定一等奖 10 人，二等奖 20 人，现在将一等奖中最后4人调整为二等奖，这样得二等奖的学生平均提高了1分，得一等奖的学生平均分提高了3分，求原来一等奖平均分比二等奖平均分多（    ）分。

❞

「答案分析」

这题可以设未知数用方程来解答，也可以不用。

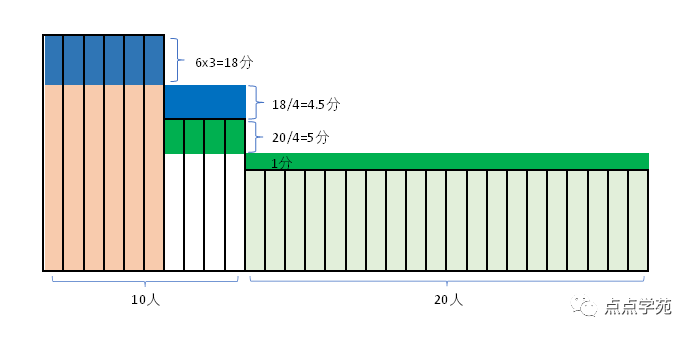
我们像上面那样画个示意图，6个一等奖分在一组，后面的4个一等奖分在另一组，20个二等奖的分在另一组。

前6个的平均分降低了3分，那么就要将6x3=18分分给后面4个人，每人可分18/4=4.5分。

20个二等奖的平均分提高了1分，这20分是后4个一等奖的分匀过来的，后4个一等奖的平均每人分摊了20/4=5分。

因此，原有平均分，一等奖比二等奖高分。

❝

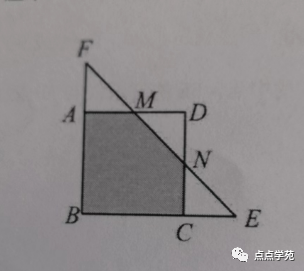
9.如下图，正方形 ABCD 与等腰直角三角形 BEF 放在一起，M、N点为正方形的边的中点，阴影部分的面积是 21 平方厘米，正方形ABCD 的面积是(     )平方厘米。

❞

「答案分析」

取BC中点和AB中点，原有正方形被分割成了4个小正方形，

如果将每个小正方形的面积看作2份，则阴影部分刚好是7份。

因此，正方形的面积就是平方厘米。

❝

10、甲、乙、丙三辆车同时从A地出发到B地去，出发后12分甲车超过了一名长跑运动员，4分后乙车也超过这名运动员，又过了4分丙车也超过了这名运动员。已知甲车每分走1000米，乙车每分走800米，丙车每分钟走（    ）米。

❞

「答案分析」

依题意，当乙车追上运动员的时候，运动员又走了

当丙车追上运动员的时候，运动员又走了800米。

因此，丙车的速度就是：

也就是说，丙车每分钟走680米。

---

添加 家长论坛微信