分析：注意区别到达的楼层和走过的楼层，这是两个不同的概念，很容易造成典型错误：两只青蛙相差一层楼，所以答案是8楼。

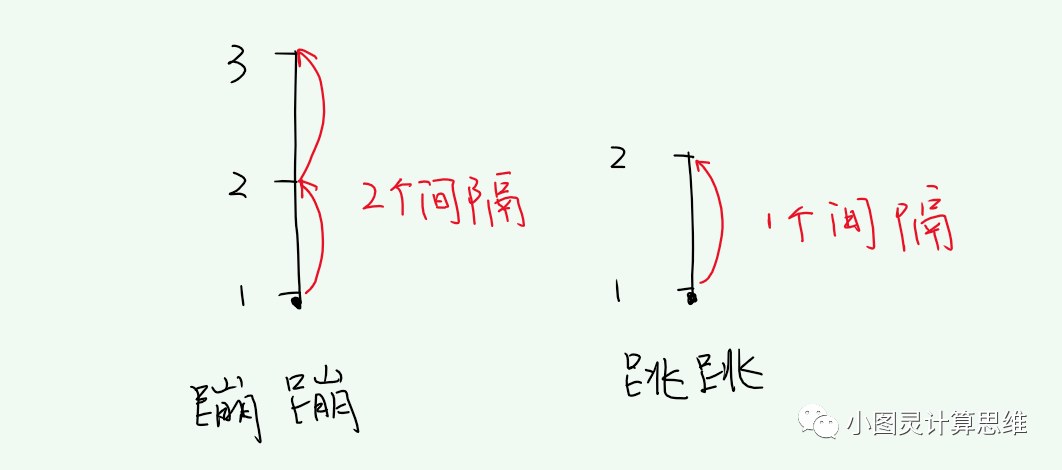
蹦蹦走2个间隔的时间 = 跳跳走一个间隔的时间。那么当“蹦蹦”跳到 9 楼的时候，走过了8个间隔；此时跳跳走了4个间隔，到达5楼。

解：(9 - 1）/ 2 + 1 = 5(楼)

分析：注意区别锯木的段数和锯木的次数

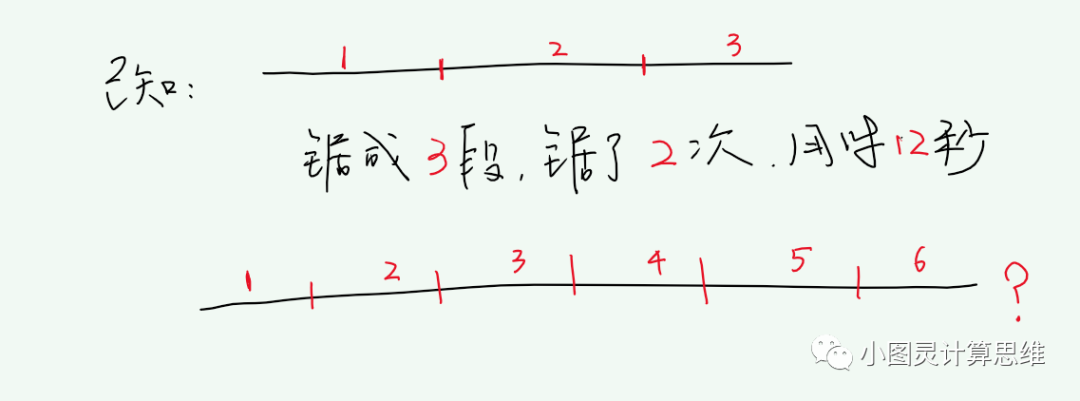
锯木3段，锯了2次，用时12秒；锯1次用时：12 / 2 = 6(秒)；那么：

锯成6段，锯了5次，用时：5 * 6 = 30(秒)

解：12 / (3 - 1) * (6 - 1)= 30(秒)

分析：典型的植树问题，属于间隔问题的线性问题。

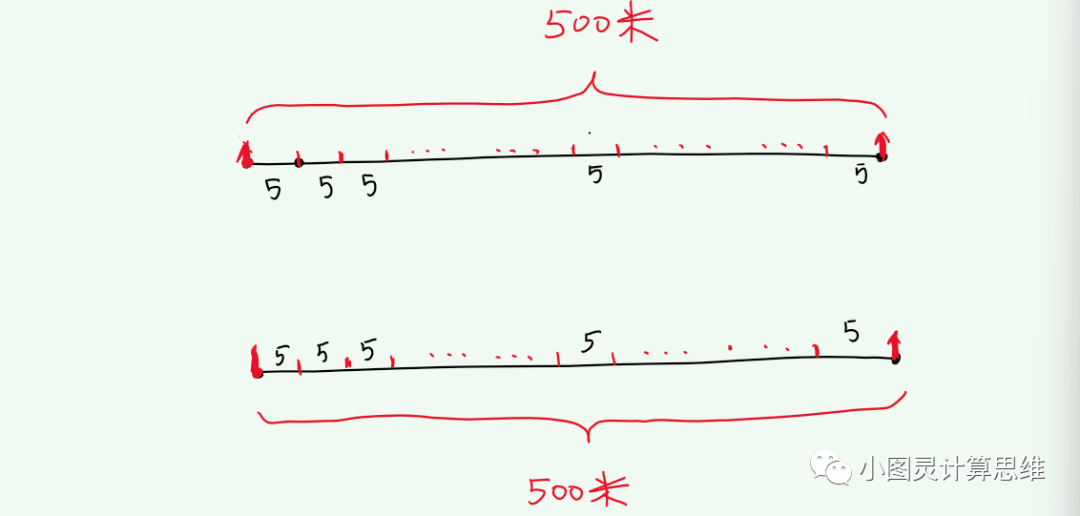
线性问题：把问题抽象成一条直线，间隔数 = 点数 - 1；点数 = 间隔数 + 1

所以：500米的路需要种的树有：500 / 5 + 1 = 101(棵)

两边都要种，所以，一共要种：(500 / 5 + 1) * 2 = 202(棵)

思考：既然两边都要种树，那能这样算吗：500 * 2 / 5 + 1 ？

解：(500 / 5 + 1) * 2 = 202(棵)

分析：典型的排队问题，这类题强烈推荐画图，数无形时少直觉。

根据图示，

中间的人数 = 总人数 - 从头到大李的人数 - 从尾到小李的人数

                  = 30 - 5 - 3 = 22(人)

解：30 - 5 - 3 = 22(人)

分析：典型的环形问题：把问题抽象成一个圆，间隔数 = 点数。注意区分顺时针与逆时针。这类题强烈推荐画图。

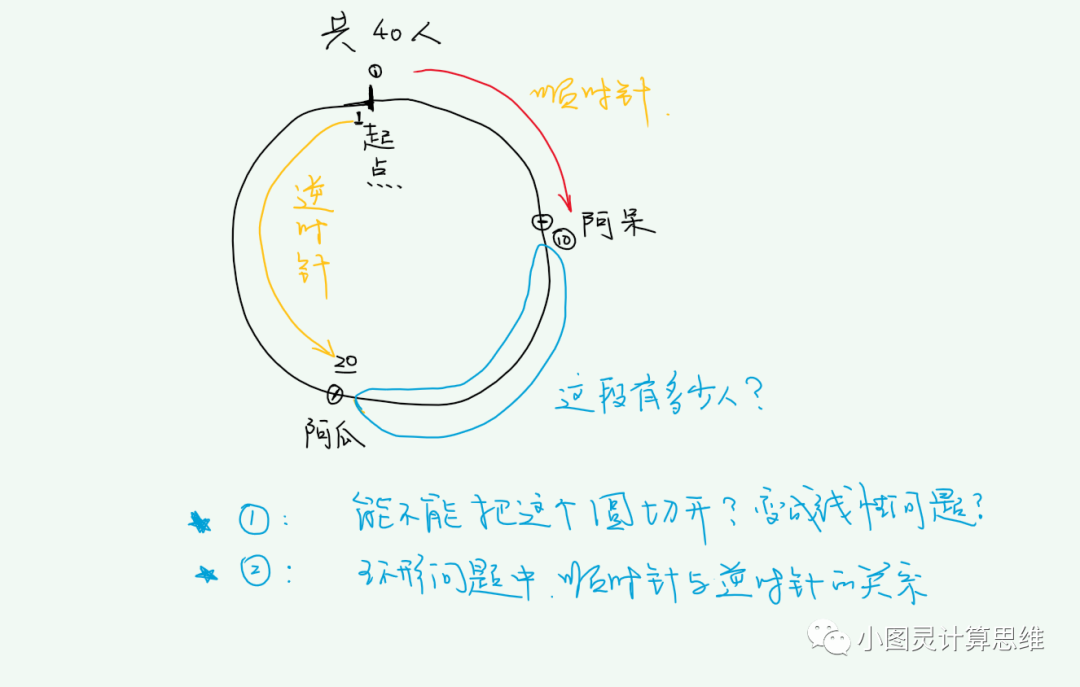
图中说到2个思路：

1. 能不能把这个圆切开，变成线性问题？（转化思想）

2. 环形问题中，顺时针与逆时针的关系？

1. 能不能把这个圆切开，变成线性问题？当然可以，这是很关键的数学思想，把不熟悉的问题转换成熟悉的问题。转换后问题同第4题，但注意处理细节。

中间的人数 = 总人数 - 顺时针编号 - 逆时针编号 + 1

                                   = 40 - 10 - 20 + 1 = 11(人)

为什么+1 ？从圆展开成线段，起点变成了线段的两端，相当于多加了一个人

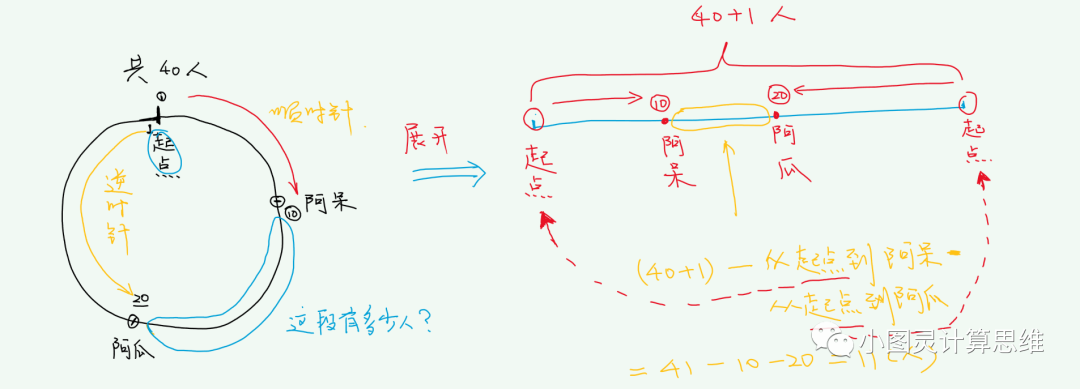
2. 环形问题中，顺时针与逆时针的关系？

顺时针编号 + 逆时针编号 = 总人数 + 1

为什么+1 ？因为第一个人在顺时针编号时算了一次， 逆时针编号又算了一次

中间的人数 = 总人数 + 1 - 顺时针编号 - 逆时针编号 

                  = 40 - 10 - 20 + 1 = 11(人)

逆时针看的话中间隔的人数：总人数 - 顺时针间隔的人数 - 阿呆 - 阿瓜

40 - 11 -1 - 1 = 27(人)

解：40 - 10 - 20 + 1 = 11(人); 40 - 11 -1 - 1 = 27(人)

分析：4人一横排，共30横排；两横排间距1米，共29个间隔

解：(120 / 4 - 1) * 1 = 29(米)

分析：先分析出一条铁索需要多少个铁环，然后乘以5就好了

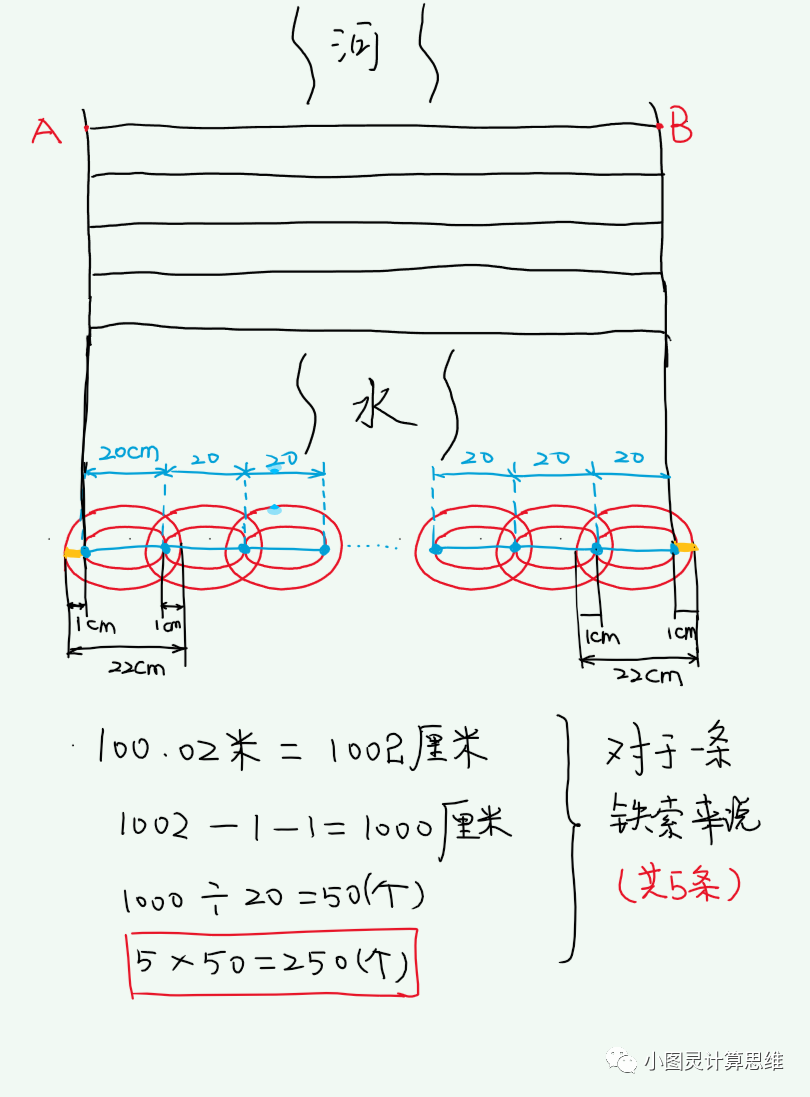
如上图，对于一条铁索来说，首先需要减去2厘米（两个黄色小线段），桥长100.02米，即10002厘米，减去左右两边的1厘米，剩10000厘米；再计算出两个蓝点之间的距离为20厘米（22 - 1 - 1），即：铁环长度减去2个铁环的粗

解：(100.02 * 100 - 2) / (22 - 1 - 1) * 5 = 2500(个)

分析：图示法更便捷，根据题中已知条件，将其转化为下图：

如图所示，吉吉和婧婧之间有1名同学。

解：1名

分析：图示法更便捷，根据题中已知条件，将其转化为下图：

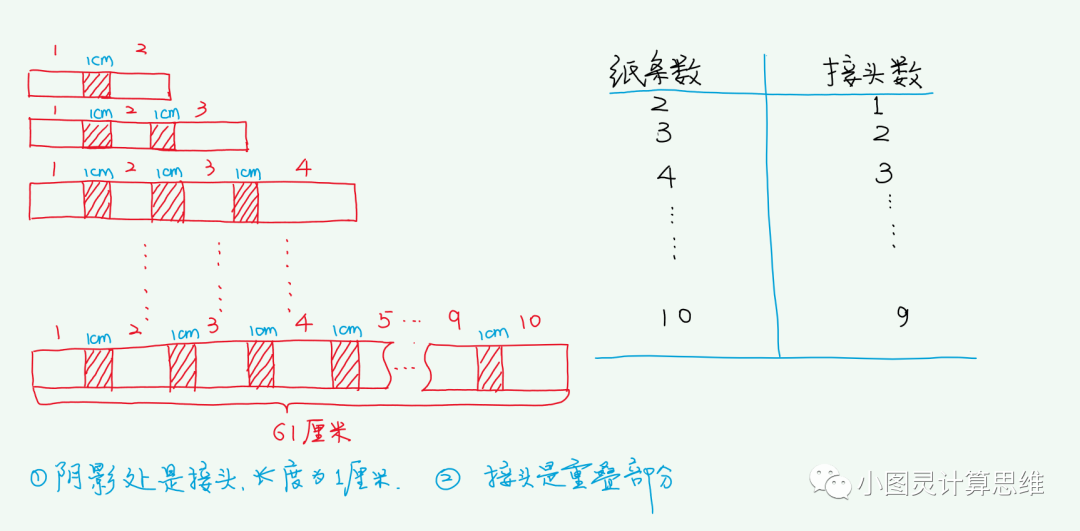
在原来的总长61厘米中，重叠处只计算了一张纸条的。如果不重叠的话还需要加上原来被忽略的部分。

即：10张纸条不重叠的长度为：61 + 1 * (10 - 1) = 70厘米

解：(61 + 1 * (10 - 1)) / 10 = 7(厘米)。

分析：先求出有几个大间隔，然后再算每个间隔里的小间隔里的点数，注意处理两个端点。

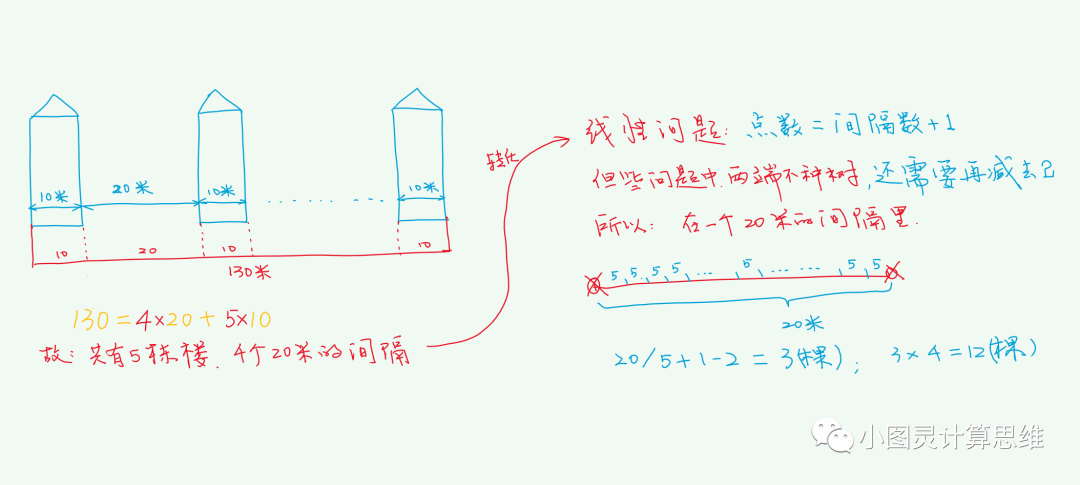
共有几栋楼：(130 - 10) / (10 + 20) + 1 = 5(栋)

大间隔数 = 点数 - 1 = 5 - 1 = 4

一个小间隔里的树数 = 间隔数 - 1 = (20 / 5) - 1 = 3(棵)

解：(130 - 10) / (10 + 20) + 1 = 5;  

       (20 / 5 - 1 ) * 4 = 12(棵); 

       12 * 10 = 120(分钟).

分析：本题看似复杂，其实画图可以转化为之前学过的排队问题。

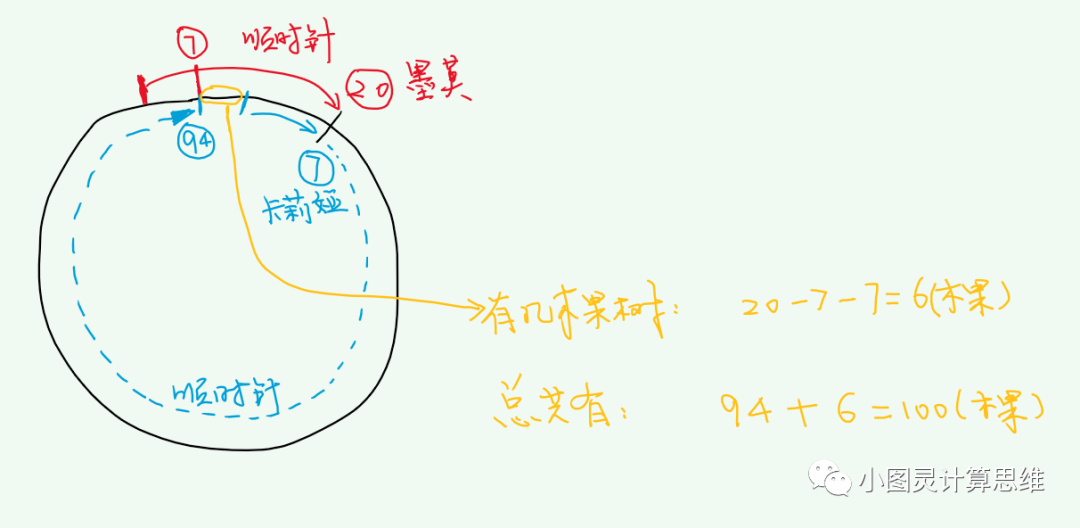
黄色部分是卡利亚还没数过的树，有：20 - 7 - 7 = 6(棵)

那么，树总数 = 卡利亚数过的树 + 卡利亚还没数过的树 = 94 + 6 = 100(棵)

解：94 + (20 - 7 - 7) = 100(棵)