2022中国国家队选拔考试第一题的来龙去脉

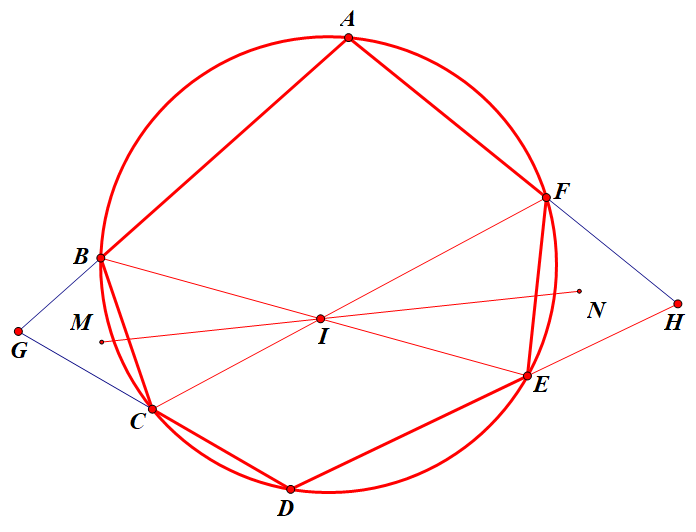
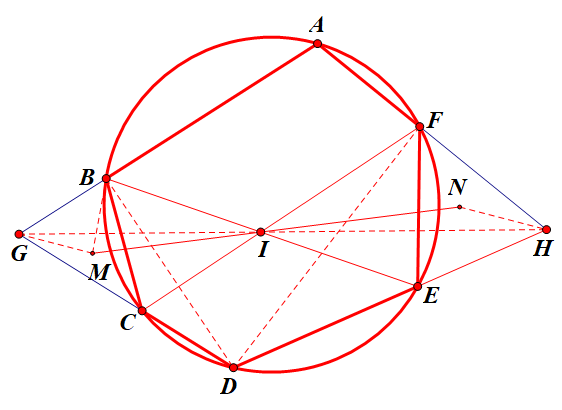
1、圆内接凸六边形ABCDEF中,AB交CD于G,AF交DE于H,M,N为△BCG、EFH的外心。
证明:BE,CF,MN三线共点。
网络上已经有很多高手给出了本题的解法,本文拟记录一下本人对此题的思考过程,并整理见到的各个高手的解答。并作简单评述。然后挖掘本题的来源及各个解法的本质,希望整理出此题的来龙去脉、前世今生。
首先画出准确的图形,图形很好画。设I为BE、CF交点。
其次挖掘图形的基本性质,圆内接六边形性质不太多,
最有名气的性质就是帕斯卡定理:圆内接六边形
对边交点,凡三点共线。对六边形ABEDCF由此定理
即得GIH共线。这个结论很可能有用。对于圆心M,
要么用OM为BC中垂线,要么用MB=MG=MC,要么用圆心角
为圆周角的二倍。但似乎都不太好用。
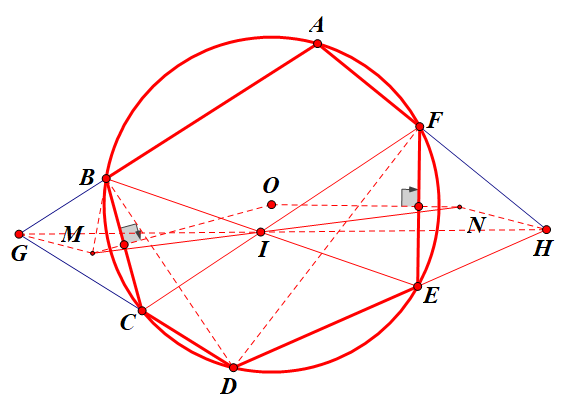
然后从结果入手,需证MN,BE,CF三线共点。即证MIN共线。
感觉直线MN、MI都不好描述。也就没法证明MN过I了。
再次回到已知图形中去,挖掘图形的性质。重点研究外心M、N,
加上前面得到GIH共线。由对称性,GM、HN应该具有类似的性质,
结合准确的图形,可以发现似乎有GM//HN,即圆M、圆N关于I位似。进而即得MIN共线。
欲证明GM//HN,即圆M、圆N关于I位似,即证GM/HN=GI/IH。
我对帕斯卡定理结构还是比较熟悉的,我的理解是,帕斯卡定理结构的本质是一个恒等式。
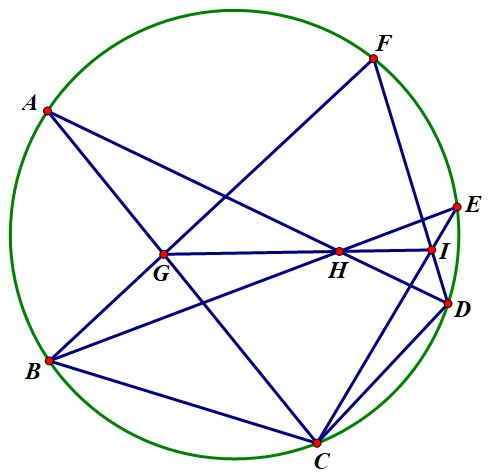
即如图所示的圆内接六边形
ACEBFD,GIH共线,且有

事实上,此结论可以和A无关,
可以隐去AC,AD,
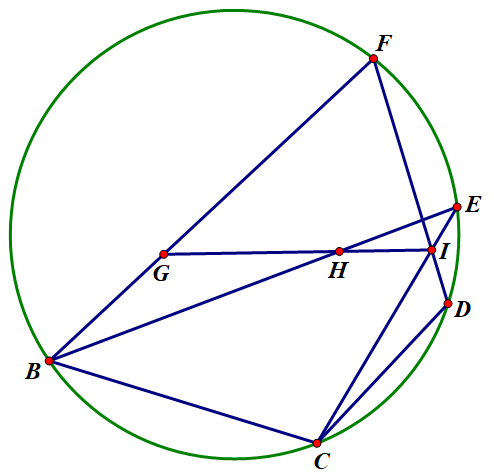
即如图,有上述恒等式。
可以理解为退化的六边形BGHIDC相间三边乘积相等。
由正弦定理即可证明。
此恒等式叶中豪老师经常提到,可以说是帕斯卡定理结构的精髓所在,
由此结论即可证明帕斯卡定理。
凭感觉,两个比例式应该是等价的。这个不难证明。
由正弦定理:

从而需证

此即为此帕斯卡结构中的恒等式。
将上述思路整理一下,可以发现不需要使用帕斯卡定理,
只要使用正弦定理,由同一法或者利用对称性即可得证。
具体证明过程如下:
证明:
设BE,CF交GH于I,由正弦定理:

从而两圆关于I点位似,则MIN共线,
对称的,有CIF共线,
从而BE,CF,MN共点于I。
上述证法是按我的思路写的,为第一种证法。网上各路高手也纷纷给出了精彩纷呈的解法。
金春来老师指出这是一个经典的问题,他三年前给学生讲过,他的证明如下,此为证法二。
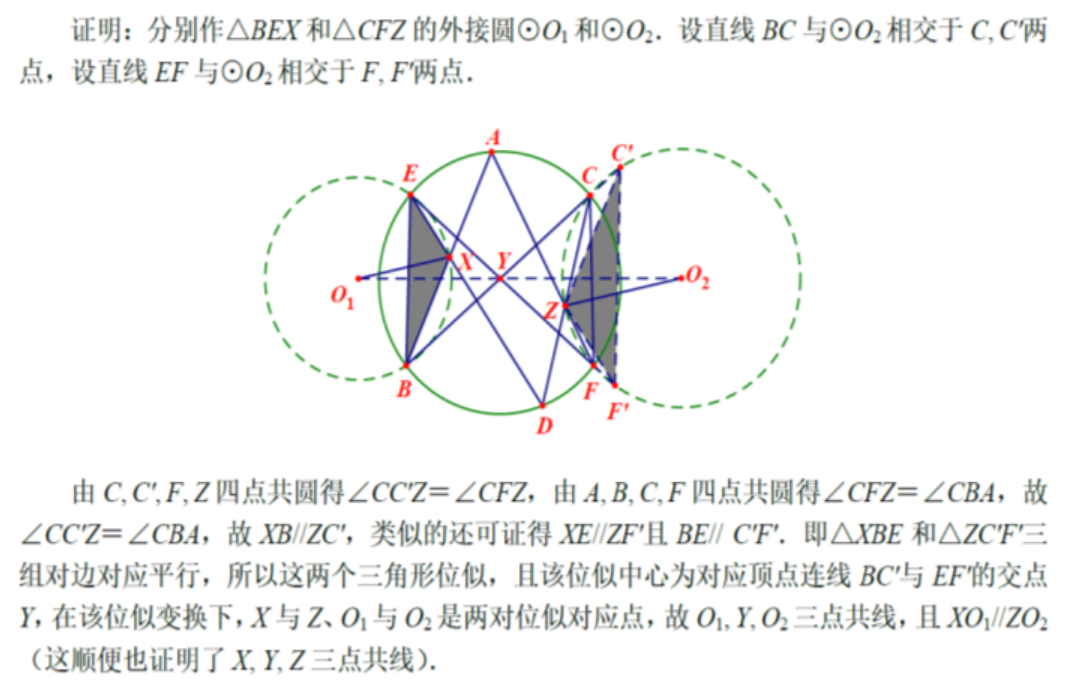
他的基本思路是利用三角形的位似证明的三点共线。
姚佳斌老师指出,此题等价于他前段时间在我们爱几何上发表的下题:
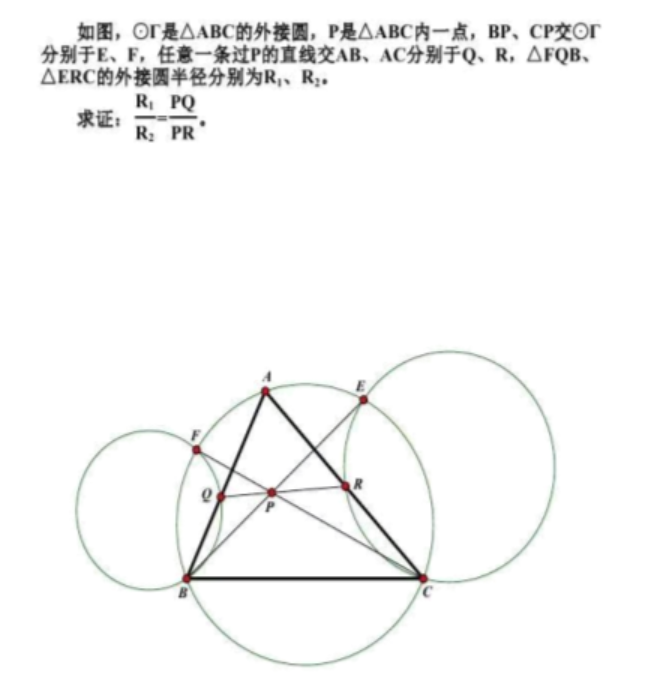
顾冬华老师对姚佳斌老师这个题的证明辅助线如下:
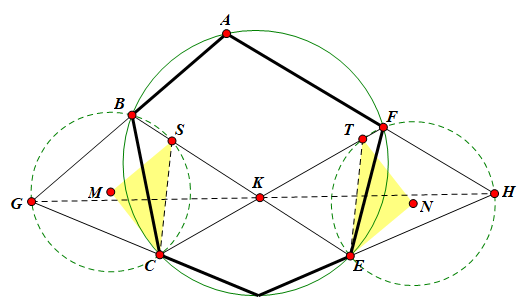
不难发现,顾冬华老师和金春来老师英雄所见略同,都是作出两个圆与对边交点,使用位似证明的三点共线,两种解法异曲同工,基本算是同一种解法。
占岩老师也给出了他的解答,如下。

占岩老师一向文思敏捷、惜墨如金,前面估计省去了sin,读起来有点拗口。他的大体思路估计和我的类似,也是通过正弦定理计算完成的。不过他是通过证明和相等的两组锐角正弦比相同得到等角的。此为证法三。
赵力医生给出了几篇参考文献[1][2],文献指出此问题为Dao Thanh Oai于2014年贴出的如下结论(有人称为Dao定理):
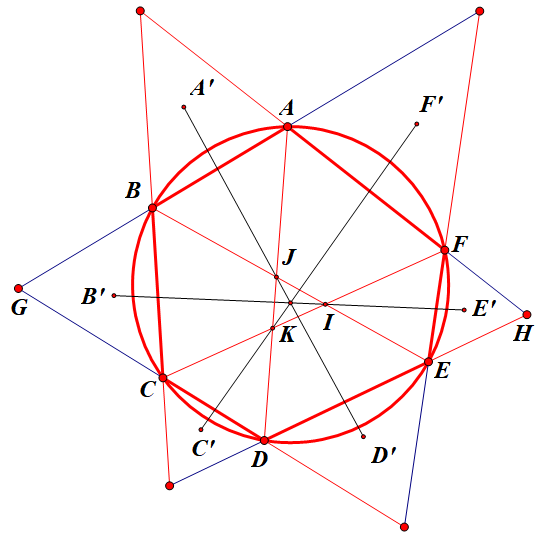
2、如下图,圆内接六边形交成的六个小三角形,相对三角形外心连线共点。
试题1为试题2的一个引理。有了1,结合角元塞瓦定理即可证明2.
当然此类问题都和帕斯卡定理有关。下面介绍帕斯卡定理的常见的三种证明方法。
3、帕斯卡定理:圆内接六边形对边交点共线。
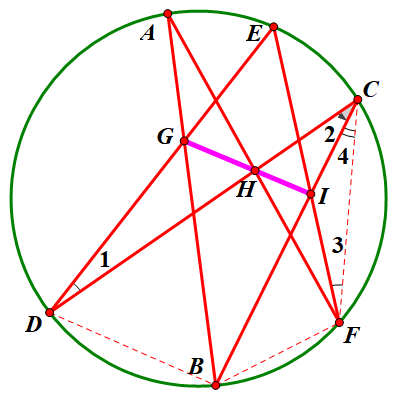
证法一:设GI交CD,AF于H,H',由正弦定理:
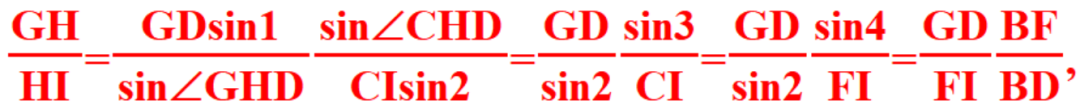
由于此表达式关于DC,FA对称,故H,H'重合,即结论成立。
证法二:
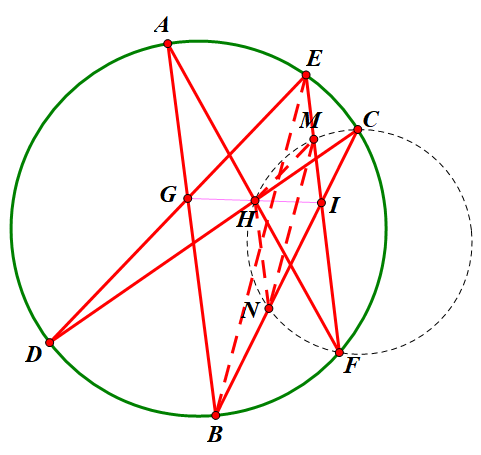
∠DEF=∠DCF=HMF,
∴DE//HM,
同理HN//AB,MN//EB,
∴△GBE与△HNM位似且I为位似中心,
∴GHI共线。
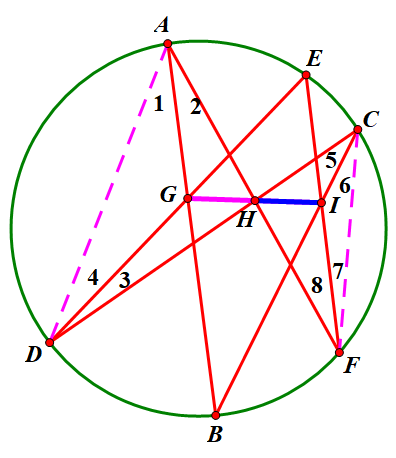
证法三:设各角如图,显然有
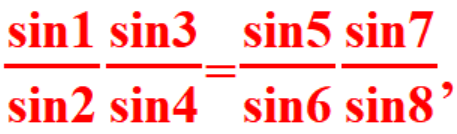
结合角元塞瓦得
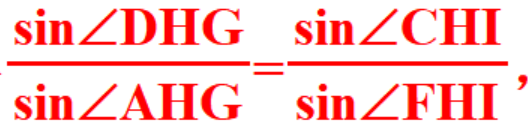
故∠DHG=∠CHI,则GHI共线。
不难发现,题1的三种证明恰好与帕斯卡定理的三种证法对应,思路和手法几无二致。这不是巧合,其实很多难题的证明或明或暗的来源于一些经典定理的证明。这也展示了大定理的威力,所谓钻之弥深,仰之弥高。大定理的各种证明都蕴含着相应的精妙思路,灵活运用这些方法往往能够解决一些看似新颖的难题。所以对于大定理,我们不能只知道结论,也不能满足于了解一种证法,还要掌握多种证法,并在解题中发现其本质,灵活使用这些证法来解决一些“新题”。
参考文献
[1] 《A Purely Synthetic Proof oed with a Cyclic Hexagon》 Telv Cohl Forum Geometricorum Volume 14 (2014) 261–264.
[2] Dao’s Theorem on Six Circumcenters associated with a Cyclic Hexagon, Nikolaos Dergiades,
Forum Geometricorum Volume 14 (2014) 243–246.

2022年IMO中国国家集训队测试






全部 0条评论