1.  跑步训练(2020 年试题A)

【问题描述】
小明要进行一个跑步训练。初始时，小明体力充沛，体力值计为10000。小明跑步时每分钟损耗600体力值。小明休息时每分钟增加300体力值。体力值的损耗和增加都是均匀变化的。小明打算跑一分钟，休息一分钟，再跑一分钟，再休息一分钟，如此循环。 如果某个时刻小明的体力值变为0，他就停止训练。
请问小明在多久后会停止训练。为了使答案为整数，请以秒为单位输出答案。答案中
只填写数字,不填写单位。
[提示]
本题可以采用模拟法，不过需要注意两点： 一是题目要求以秒为单位；二是体力值必须变为0。所以本题的计算可以分为以下两部分。
①体力值大于600时，可以持续1分钟的体力消耗，则模拟损耗600体力值，再增加300体力值，一共经过120秒，循环得到时间。
②当体力值小于600且不为0时，每秒消耗10体力值，则剩余时间为体力值/10，直到体力值为0。

2.  合并检测(2020年试题C)

【问题描述】
某病毒最近在A国蔓延，为了尽快控制该病毒，A国准备给大量民众进行病毒核酸检测。然而，用于检测的试剂盒紧缺。为了解决这一困难，科学家想了一个办法: 合并检测，即将从多人(k个)处采集的标本放到同一个试剂盒中进行检测。如果结果为阴性，则说明这k个人都是阴性，用一个试剂盒即可完成k个人的检测。如果结果为阳性，则说明其中至少有一个人为阳性，需要将这k个人的样本全部重新独立检测(从理论上看，如果检测前k-1个人都是阴性，则可以推断出第k个人是阳性，但是在实际操作中不会利用此推断，而是让k个人独立检测)，加上最开始的合并检测，一共使用了k+1个试剂盒完成了k个人的检测。A国估计被测民众的感染率大概是1%，且呈均匀分布。请问k取值多少最节省试剂盒?
[提示]
本题相对比较抽象，可以采用简单的列数字的方法查看数字k的变化情况，如下表所示。

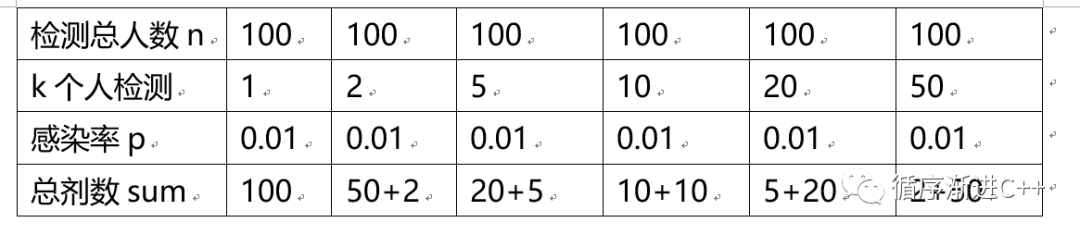
从上表的数据可以看出，总剂数的变化随着k的增长呈现出由大到小，再由小到大的变化过程。因此，本题其实就是求在k增长的过程中sum是最小值时的k值。理解了这个问题，就成比较容易求解了，让k从1遍历到100，根据公式求sum的最小值，如果存在最小值，则记录一个k的值。

3.上期答案——完全二叉树求值

完全二叉树从上到下，从左到右顺序存储，深度为1的层1个权值，深度为2的层是2个权值，深度为3的是4个权值，深度为4的层8个权值……

【参考程序1】——申茂生答案（代码最简单，效率也最高）

#include <iostream>
using namespace std;
int main()
{
     int n,sum=0,max=0,depth;
     cin>>n;
     int num[n];
     for(int i=1,j=1,k=0;k<n;k++)
  //i为该深度所含的数的个数，
  //j为深度，k为当前数的下标 
     {
         cin>>num[k];
         sum+=num[k];//累加该深度所有数的和 
         if(sum>max)//最大值 
         {
             max=sum;
             depth=j;//记录深度 
         }
         if(k==(1+i)*j/2-1)//k等于该深度最后一个数的下标 
         {
             i*=2;//个数乘二 
             j++;//深度加一 
             sum=0;//重新开始累加
         }
     }
     cout<<depth;
}

参考程序二——和参考程序一是同一个思路，但是代码写复杂了

int main()
{
 int n;
 cout<<"input n:"; //可以省略 
 cin>>n;
 int *ar=new int[n];//长度是n的数组
 cout<<"input "<<n<<"nums:" ;//可以省略
 for(int i=0;i<n;i++)
 cin>>ar[i];   //输入n个权值
 int sumMax=0;//最大权值 
 int i=1; //二叉树的深度
 int nodes;// 每层结点的个数 
 int sum;//每层权值之和
 int nT=0;//总的结点个数 
 int k;//存储最大权值的深度 
 while(nT<n)
 {   
     sum=0; 
  int nodes=pow(2,i-1);  //每一层有2的n-1次幂个结点 
  for(int j=nT;j<(nT+nodes<n?nT+nodes:n);j++)//每一层结点的个数 
   sum+=ar[j];  //本层的权值 
  if (sum>sumMax)
  {
      k=i;
      sumMax=sum;
  }
  nT+=nodes; //总的结点数加上本层的结点数 
  i++;//深度加1 
  } 
  cout<<k<<endl;
}

【参考程序3】——杨泽天答案（pow函数和log2函数还自己写出来了，可以调用cmath文件中的库函数）

#include <iostream>
using namespace std;
int pow(int n,int i){
int ret = 1;
for(int j=0;j<i;j++)
ret *=n ;
return ret;
}

int log2(int n){
int ret = 0; 
while (1){
n/=2;
if(!n) break;
ret++;
}
return ret;
}
int main(){
int n;
cin >> n;
int* num = new int[n];
for(int i=0;i<n;i++){
cin >> num[i];
}
// 从最后一行开始算  边算边找最大值
int deep = log2(n+1);
int maxdp = log2(n+1);
int max_ = 0;
// 最后一行开始   一直到第一行  每一行的个数为2^(i-1) 
for(int i=deep;i>=1;i--){
// 找到他们对应的结点的下标   第 i 行第一个对应的是 2^(i-1)   最后一个对应的是  2^i-1
int sum = 0;
for(int j=pow(2,i-1)-1;j<=pow(2,i)-2;j++){
sum += num[j];
}
if (sum >= max_){
max_ = sum;
maxdp = i;
} 
cout << "第" << i << "行的和为：" << sum << endl;
}
cout << "最大值为：" << max_ << endl;
cout << "最大值所在的最小深度为：" <<  maxdp << endl;
return 0;
}

【参考程序4】——宋秀杰答案

#include <stdio.h>
#include <math.h>
int main()
{
int n,depth,max=0,sum;
scanf("%d",&n);
int a[n],i,j;
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
for(i=1;i<=floor(log(n)/log(2))+1;i++){//floor(log(n)/log(2))+1求完全二叉树n个节点深度是多少 
sum=0;
    for(j=pow(2,i-1);j<pow(2,i);j++){//pow(2,i-1)每行的开始下标，pow(2,i)-1每行的结束下标 
       sum+=a[j];
    if(j==n) break;//当到最后一个节点时结束循环 
}
if(sum>max){
max=sum;
depth=i;
}
}
printf("%d",depth);
return 0;
} 

4.上期答案——等差数列

（这个题目简单，都是一个思路） 【参考程序1】——杨泽天答案（自己写了最大公约数函数、快速排序函数）

#include <iostream>
using namespace std;
void QuickSort(int *array,int low,int high); //快速排序 
int gcd(int a,int b); //最大公约数 
int main(){
     int n;
     cin >> n;
     int* num = new int[n];
     for(int i=0;i<n;i++)
     cin >> num[i];
     QuickSort(num,0,n-1);
     int min = num[1] - num[0];
     for(int i=1;i<n-1;i++)
     {
         int temp = num[i+1]-num[i];
         int temp2 = gcd(min,temp);
         if (temp2 < min){
         min = temp2;
        }
     } 
     //min是公差 
     // an = a1 + (n-1)d ——  n=(an-a1)/d+1 等差数列项数公式 
     cout << (num[n-1] - num[0])/min + 1 << endl; 
     return 0;
}

void QuickSort(int *array,int low,int high){ //快排 
     if(low>=high){ //若待排序序列只有一个元素，返回空 
     return ;
     }
     int i=low; //i作为指针从左向右扫描 
     int j=high; //j作为指针从右向左扫描
     int key=array[low];//第一个数作为基准数 
     while(i<j){
         while(array[j]>=key&&i<j){ //从右边找小于基准数的元素 （此处由于j值可能会变，所以仍需判断i是否小于j） 
             j--; //找不到则j减一 
         }
         array[i]=array[j]; //找到则赋值 
         while(array[i]<=key&&i<j){ //从左边找大于基准数的元素 
             i++; //找不到则i加一 
         }
         array[j]=array[i]; //找到则赋值 
     }
     array[i]=key; //当i和j相遇，将基准元素赋值到指针i处 
     QuickSort(array,low,i-1); //i左边的序列继续递归调用快排 
     QuickSort(array,i+1,high); //i右边的序列继续递归调用快排 
}

int gcd(int a,int b)//求最大公约数 
{
     if (a < b){
         int temp = a;
         a = b;
         b = temp;
     }
     if(b==0) return a;
     return gcd(b,a%b);
}

【参考程序2】——申茂生答案

#include <iostream>
using namespace std;
int gcd(int a,int b)//更相减损法求最大公约数 
{
     int c=1;
     while(a%2==0&&b%2==0)
     {
         a/=2;
         b/=2;
         c*=2;
     }
     while(a!=b)
         a>b?a-=b:b-=a;
     return c*a;
}
int main()
{
     int n;
     cin>>n;
     int num[n],d[n-1];//num[n]为n个数,d[n-1]为差值 
     for(int i=0;i<n;i++)
          cin>>num[i];
     for(int i=n-1;i>0;i--)//冒泡排序法从小到大排序 
         for(int j=0;j<i;j++)
             if(num[j]>num[j+1])
             {
                 int t=num[j];
                 num[j]=num[j+1];
                 num[j+1]=t;
             }
     for(int i=0;i<n-1;i++)//将相邻两个数的差值存入 
         d[i]=num[i+1]-num[i];
     for(int i=0;i<n-2;i++)//求所有差值的最大公约数
          d[i+1]=gcd(d[i],d[i+1]);
     cout<<(num[n-1]-num[0]+d[n-2])/d[n-2];
 }

---

添加 家长论坛微信