(注.input()输入函数的括号中不允许添加任何信息)

【编程实现】

现将N（3≤N≤600）根胡萝卜全部分配给黑、白、灰三只兔子，分配规则如下：

1）黑、白、灰三只兔子必须都能分到胡萝卜；

2）黑兔子的胡萝卜数大于或等于白兔子的胡萝卜数；

3）白兔子的胡萝卜数大于或等于灰兔子的胡萝卜数；

请按照规则计算，将N根胡萝卜全部分配给三只兔子，共有多少种不同的分配方法。

例如：N = 8，按照分配规则有5种不同的分配方法，具体分配方法如下图：

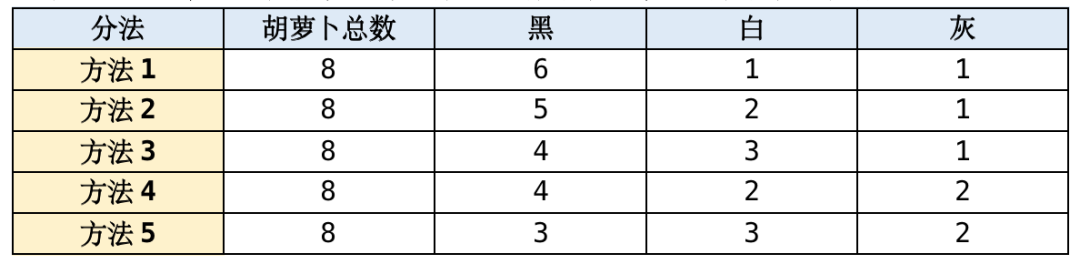
【输入描述】

输入一个正整数N（3≤N≤600），表示胡萝卜的数量

【输出描述】

输出一个整数，表示将N根胡萝卜全部分配给三只兔子，共有多少种不同的分配方法

【样例输入】

8

【样例输出】

5

【题目解析】

本题可以使用双重for循环枚举 + 计数器解决。双重for循环分别表示黑兔和白兔的萝卜数量，则灰兔数量可以确定为总数 – 黑兔 – 白兔，从而避免第三层循环。如果当前情况的数量满足题目要求，则计数器自增1。需要注意的是枚举范围，最少为1，最多还需要保证剩下的兔子至少为1。

【参考代码】

n = int(input())cnt = 0for black in range(1, n - 1):    for white in range(1, n - black):        grey = n - black - white        if black >= white and white >= grey:            cnt += 1print(cnt)

(注.input()输入函数的括号中不允许添加任何信息)

【编程实现】

某服务大厅同时开放3个窗口为客户办理业务，窗口编号分别为1、2、3。

现有N（2≤N≤50）位客户需要办理业务，客户编号为1~N，作为办理业务的先后顺序。

起初三个窗口为空闲状态，空闲的窗口会按照客户编号顺序呼叫下一位客户。

如果多个窗口同时为空闲状态，按照窗口编号顺序呼叫（1优先于2，2优先于3）。

现给出每位客户办理业务的时间（单位：分钟），请计算出N位客户全部办理完业务后，

哪一个窗口合计办理业务的时间最短，并输出最短时间。

例如：N=7，7位客户编号分别为1、2、3、4、5、6、7，

客户办理业务时间分别为3、5、2、4、7、1、6，（如下图）：

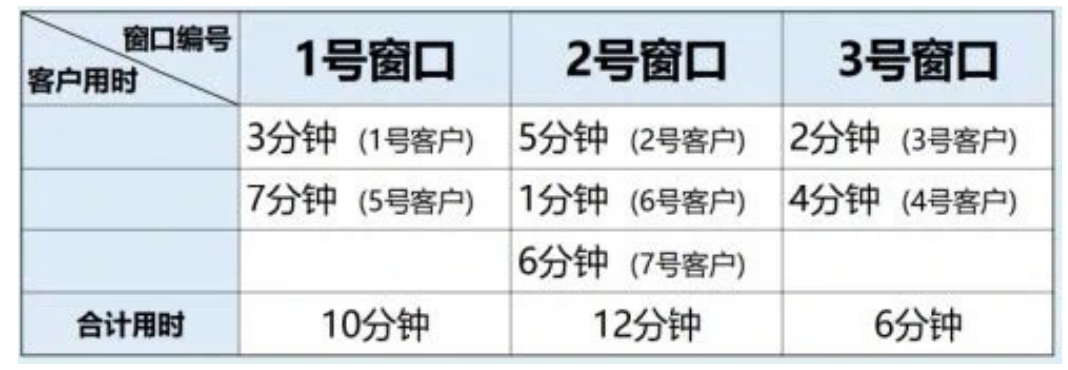
初始客户编号为1、2、3的客户分别在1、2、3窗口同时办理业务；

窗口3用时2分钟办理完3号客户的业务，变为空闲状态，并按顺序呼叫4号客户，4号客户用时4分钟；

窗口1用时3分钟办理完1号客户的业务，变为空闲状态，并按顺序呼叫5号客户，5号客户用时7分钟；

窗口2用时5分钟办理完2号客户的业务，变为空闲状态，并按顺序呼叫6号客户，6号客户用时1分钟；

6分钟后，窗口2和3同时变为空闲状态，按顺序窗口2呼叫7号客户，7号客户用时6分钟。

全部客户办理完业务后，三个窗口总用时分别为10分钟、12分钟、6分钟，用时最短的是窗口3，最短时间为6分钟。

【输入描述】

第一行输入一个正整数N（2≤N≤50），表示办理业务的客户数

第二行输入N个正整数（1≤正整数≤50），依次表示每位客户办理业务的时间，正整数之间以一个空格隔开

【输出描述】

输出一个整数，表示客户全部办理完业务，用时最短的窗口所用时间

【样例输入】

7

3 5 2 4 7 1 6

【样例输出】

6

【评分标准】

4分：能正确输出第一组数据；

4分：能正确输出第二组数据；

4分：能正确输出第三组数据；

4分：能正确输出第四组数据；

4分：能正确输出第五组数据；

5分：能正确输出第六组数据。

【题目解析1】

本题属于“模拟”问题，方法1为客户维度模拟。

假设编号为 1、2、3 的窗口的办理业务累计的时间储存在列表c中，分别为c[0]、c[1]、c[2]，第i个客户办理业务的时间为 ls[i - 1]。

对于第i个客户，需要找到一个时间结束最早的窗口，也就是办理业务累计的时间最小的（即），并给这个窗口的时间加上ls[i-1]。

最后 c[0]，c[1]，c[2] 的最小值即为答案。

【参考代码1】

n = int(input())ls = [int(i) for i in input().split(" ")]t = 1c = [0, 0, 0]for i in range(n):  if c[0] == min(c):    c[0] += ls[i]  elif c[1] == min(c):    c[1] += ls[i]  else:    c[2] += ls[i]print(min(c))