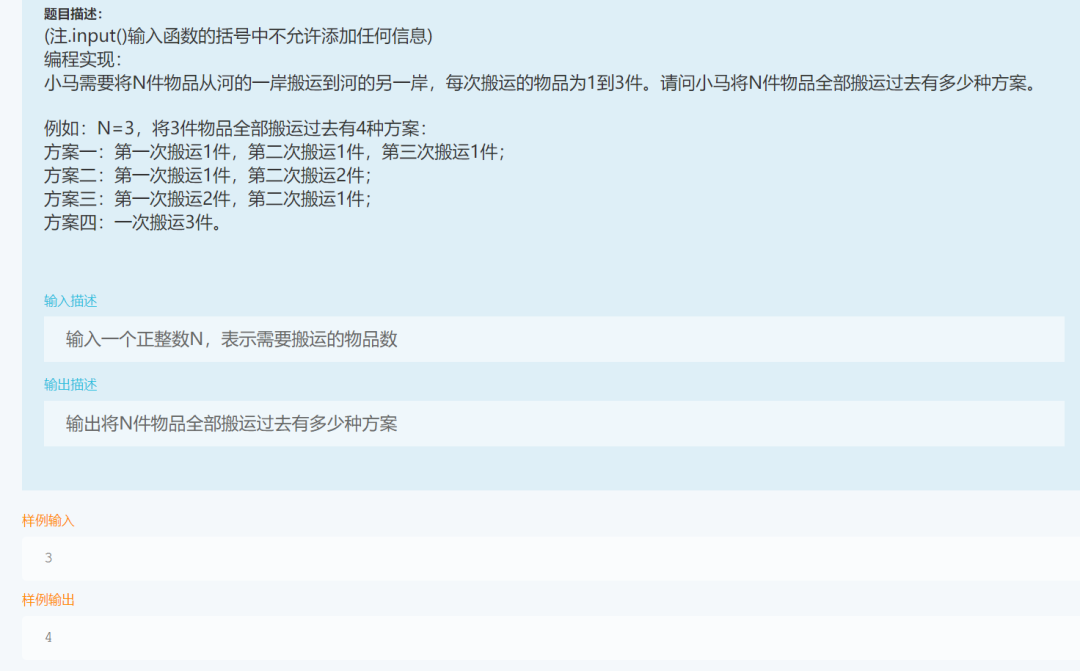
这不是组合问题，而是路径问题，一般用树来计算，树的叶子总数就是方法数。根节点是N，分-1,-2,-3三叉，到0为叶节点，统计数加1，小于0作废。

    程序代码（文本附录１）：

　　运行结果：

　　这是在矩阵中统计连通图问题，可以转化为森林统计树木数量的问题。找到一个非０点，把它变为０，然后检查上下左右是不是非０，如果是重复操作，直到上下左右都是0，统计数加1；剩下的继续检查，直到没有非０点。

　　程序代码（文本附录２）：

　　运行结果：

　　这是一道数学题，用数学语言描述：在N×M的只含有0和1的矩阵中，寻找最大边长的方阵，这个方阵只有一条对角线上的数全是1。

　　数学分析：首先检查必要条件——总和等于边长数，然后再检查两条对角线；后面的检查只需检查边长数比原来大的。

　　程序代码（递归，文本附录３）:

　　程序代码（循环，文本附录4）:

　　运行结果：

十二界蓝桥杯Python组省赛试题详解——选择题

十二界蓝桥杯青少年Python中级组省赛试题详解——编程题之一

十二界蓝桥杯青少年Python中级组省赛试题详解——编程题之二：排序

十二界蓝桥杯青少年Python中级组省赛试题详解——编程题之三：密室逃脱

十二界蓝桥杯青少年Python中级组省赛试题详解——编程题之四/八皇后问题

十一界蓝桥杯青少年Python中/高级组省赛试题详解——选择题

十一界蓝桥杯青少年Python中/高级组省赛试题详解——编程题1~3

十一界蓝桥杯青少年Python中/高级组省赛试题详解——编程题4密码表/5节气表/6最近距离

十界蓝桥杯青少年Python中/高级组省赛试题详解——编程题１～４

十界蓝桥杯青少年Python中/高级组省赛试题详解——编程题：树形绘制

　　学思营编程课堂基于蓝桥STEM86平台https://www.stem86.com，开展学编程三部曲：

Scratch（三年级以前）>>>Python（四年级以后）>>>C++（七年级以后）教育实验活动，任何人可以免费参加，打开https://xuesiying.stem86.com网页注册进入课堂，也可关注本公众号留言。

更多课程请打开“学思营”同步网站：

http://www.5xstar.com/doc.html

附录１：

N=int(input())  #输入一个正整数
c = 0 #声明方法统计数
def count(n):  #统计递归方法
    global c  #声明全局变量
    if n < 0:  #作废
        return
    elif n == 0:  #一叶节点，统计数加１，返回
        c += 1
        return
    for i in range(1,4): #每次减１到３个
        count(n-i)  #递归调用
count(N)  #执行统计
print(c)  #打印结果

附录２：

N,M = eval("["+input()+"]")  #输入矩阵行列数
lst = [ eval("["+input()+"]") for i in range(N)]  #输入矩阵
c = 0  #连通图数量
def fd(i,j,isR):  #递归统计
    '''@i行@j列@isR是否非递归调用（入口调用）'''
    global c  #声明全局变量
    if lst[i][j] > 0:  #找到一个非０点
        lst[i][j] = 0  #把这点变0
        if isR:  #如果是入口调用，连通图数量加1
            c += 1
        if i > 0:  #向上走
            fd(i-1,j,False)
        if i < N - 1:  #向下走
            fd(i+1,j,False)
        if j > 0:  #向左走
            fd(i,j-1,False)
        if j < M -1:  #向右走
            fd(i,j+1,False)
for i in range(N):  #遍历矩阵
    for j in range(M):
        fd(i,j,True)
print(c)  #打印结果

附录３：

N,M = [ int(d) for d in input().split(" ")]  #输入矩阵行列数
lst = [[int(d) for d in input().split(" ")] for i in range(N)]  #输入矩阵
c = 0  #最大奖品数
def square(i,j):  #递归方阵统计
    global c  #声明全局变量
    if i+c >= N or j+c >= M:  #越界检查
        return
    s = sum([sum(lst[k][j:j+c+1]) for k in range(i,i+c+1)])  #统计方阵１的总数
    if s!= c+1:  #如果总数不等于边长
        return
    for k in range(0,c+1):  #检查正向对角线
        if lst[i+k][j+k] == 0:
            break
    else:  #如果正向对角线全1
        c += 1  #最大奖品数加1
        square(i,j)  #递归调用
        return  #返回，不执行后续语句
    for p in range(c,-1,-1): #检查负向对角线
        if lst[i+p][j-p] == 0:
            break
    else:
        c += 1
        square(i,j)
for i in range(N):  #遍历矩阵
    for j in range(M):
        square(i,j)  #递归调用
print(c)  #打印结果

附录４：

N,M=[int(i) for i in input().split(" ")]   #输入矩阵行列数
list1=[[int(j) for j in input().split(" ")] for i in range(N)]  #输入矩阵
maxCountOne=0 #最大奖品数
for BC in range(1,min([N,M])+1):  #遍历边长可能值
    BCbreak=False  #当前边长是否终止内循环
    for j in range(N-BC+1):  #遍历当前边长方阵
        for i in range(M-BC+1):
            countOne=0  #元素1统计
            list_1=[]  #当前边长方阵收集器
            for l in range(BC):  #逐列复制方阵
                list_1.append(list1[j+l][i:i+BC])
                countOne+=sum(list_1[l])  #统计１列
            if countOne==BC:  #统计值符合必要条件——等于边长
                for k in range(BC):
                    if list_1[k][k] == 0:
                        break
                else:   #如果正向对角线全1
                    maxCountOne,BCbreak=BC,True  #最大奖品数等于边长，终止当前边长检查
                    break  #中断行循环
                for k in range(BC):  #检查正向对角线
                    if list_1[k][BC-k-1] == 0:
                        break
                else:
                    maxCountOne,BCbreak=BC,True
                    break
        if BCbreak:  #中断列循环，进入下一个边长数的循环
            break
print(maxCountOne)  #打印结果

---

添加 家长论坛微信