真题解析 || 第十四届蓝桥杯11月STEMA
3月STEMA考试即将来袭
俗话说得好
知己知彼,百战百胜
快来看看真题
了解一下对手吧

执行 cout << 5 / 3; 语句后,输出的结果是( )。
A、0
B、1
C、2
D、3
【答案】B
【解析】在C++中,int类型/int类型=int类型,会直接丢弃小数点即小数点后面的部分。

执行以下代码,输出的结果是( )。
char a[6]={'a', 'b', 'c', 'd'};
cout<<sizeof(a);
A、4
B、6
C、8
D、12
【答案】B
【解析】sizeof(数组名),返回数组的长度(所占的字节数,不是数组元素个数),一个char 类型变量占一个字节。

关于C++中的一维数组,以下描述正确的是( )。
A、数组中的元素类型可以不相同
B、数组在内存中有一段连续的单元
C、数组中的最后一个元素的下标(索引)为 -1
D、静态数组中的元素的个数可以大于数组初始时设定的长度
【答案】B
【解析】数组是一定数量的同类型变量组成的整体,在内存中占用一段连续的存储单元,数组中第一个元素的下标为 0,最后一个元素的下标为数组长度-1,静态数组(即我们经常使用的数组,例如 int a[10010]; )的长度是预先定义好的,在整个程序中,一旦给定大小后就无法改变。

以下关于 while 和 do...while 循环语句描述不正确的是( )。
A、do...while 的循环条件可以是 1
B、while 的循环体可以是复合语句
C、do...while 的循环体至少执行一次
D、执行 do...while 语句,首先判断循环条件,当满足循环条件,开始执行循环体中的语句
【答案】D
【解析】while 语句,先判断循环条件,当满足循环条件,才会执行循环体中的语句;
do...while 语句,先执行一次循环体中的语句,再判断循环条件,当满足循环条件,才会继续执行循环体中的语句。

已知:int a, b = 5, *p = &a ,下列表达式哪一个可以将 b 赋值给 a ?( )。
A、*p = *&b;
B、a = *p;
C、a = &b;
D、a = **p;
【答案】A
【解析】&a 表示变量 a 的地址,int *p; 表示定义一个指向 int 类型变量的指针p (即用来存储某一个 int 类型变量的内存地址)。
解引用运算符 * 的作用是将一个指针解引用,也就是获取指针指向内存地址的内容,定义一个指针之后使用 *p 表示 p 这个指针指向的内存地址中存放的内容,即*p 表示一个变量,存储的是一个值。
A 选项中, &b 表示变量 b 的地址, *&b 等价于变量 b , int *p = &a; 表示定义一个 int 类型的指针,初始值为变量 a 的地址, *p 等价于变量 a ,那么 *p = *&b; 等价于将变量 b 赋值给变量 a 。
B 选项中, a = *p; 等价于将变量 a 赋值给变量 a 。
C 选项中, a = &b; 等价于将变量 b 的地址赋值给变量 a ,类型不匹配。
D 选项中, a = **p; 将指针 p 是一个一级指针,不能被解引用两次。
【题目描述】
有一块矩形蛋糕,小明从蛋糕的正上方横向和纵向各切 N 刀(1 < N < 100),每刀互不重合。计算出蛋糕被切割成了几块。
例如:N = 2,蛋糕被切割成 9 块。

【输入格式】
输入一个正整数 N(1 < N < 100),表示蛋糕被横向和纵向各切割的刀数。
【输出格式】
输出一个整数,表示蛋糕最后被切割成了几块。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
cout<<(n+1)*(n+1)<<endl;
return 0;
}
【解析】
纵向切割 n 刀将蛋糕分成 n + 1列,再横向切割 n 刀会将蛋糕分成(n+1)*(n+1)块。
【题目描述】
请编写程序:
当输入的大写字母为 "A" 时,则输出 "Apple";
当输入的大写字母为 "B" 时,则输出 "Banana";
当输入的大写字母为 "O" 时,则输出 "Orange";
当输入的大写字母为 "P" 时,则输出 "Pear"。
【输入格式】
输入 A、B、O、P 中任意一个大写字母。
【输出格式】
输出一个字符串,表示大写字母对应的英文单词(单词首字母大写)。
#include<bits/stdc++.h>
using namespace std;
int main()
{
char c;
cin >> c;
if(c=='A')
cout<<"Apple"<<endl;
if(c=='B')
cout<<"Banana"<<endl;
if(c=='O')
cout<<"Orange"<<endl;
if(c=='P')
cout<<"Pear"<<endl;
return 0;
}
【解析】
根据读入的字符 c,输出对应的英文单词,只有四种情况且情况之间没有交集,直接四个 if 判断即可。
【题目描述】
某服务大厅同时开放3个窗口为客户办理业务,窗口编号分别为1、2、3。
现有N(2≤N≤50)位客户需要办理业务,客户编号为1~N,作为办理业务的先后顺序。
起初三个窗口为空闲状态,空闲的窗口会按照客户编号顺序呼叫下一位客户。如果多个窗口同时为空闲状态,按照窗口编号顺序呼叫(1优先于2,2优先于3)。
现给出每位客户办理业务的时间(单位:分钟),请计算出N位客户全部办理完业务后,哪一个窗口合计办理业务的时间最短,并输出最短时间。
例如:N=7,7位客户编号分别为1、2、3、4、5、6、7,客户办理业务时间分别为3、5、2、4、7、1、6,(如下图):
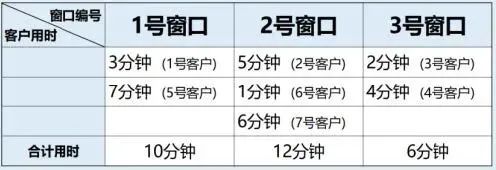
初始客户编号为 1、2、3 的客户分别在 1、2、3 窗口同时办理业务;
窗口 3 用时 2 分钟办理完 3 号客户的业务,变为空闲状态,并按顺序呼叫 4 号客户,4 号客户用时 4 分钟。
窗口 1 用时 3 分钟办理完 1 号客户的业务,变为空闲状态,并按顺序呼叫 5 号客户,5 号客户用时 7 分钟。
窗口 2 用时 5 分钟办理完 2 号客户的业务,变为空闲状态,并按顺序呼叫 6 号客户,6 号客户用时 1 分钟。
6 分钟后,窗口 2 和 3 同时变为空闲状态,按顺序窗口 2 呼叫 7 号客户,7 号客户用时 6分钟。
全部客户办理完业务后,三个窗口总用时分别为 10分钟、12分钟、6分钟,用时最短的是窗口 3,最短时间为 6 分钟。
【输入格式】
第一行输入一个正整数 N(2 ≤ N ≤ 50),表示办理业务的客户数。
第二行输入 N 个正整数(1 ≤ 正整数 ≤ 50),依次表示每位客户办理业务的时间,正整数之间以一个空格隔开。
【输出格式】
输出一个整数,表示客户全部办理完业务,用时最短的窗口所用时间。
#include<bits/stdc++.h>
using namespace std;
int n,q[10],x;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x;
int t=1;
if (q[2]<q[t]) t=2;
if (q[3]<q[t]) t=3;
q[t]+=x;
}
cout<<min(q[1], min(q[2], q[3]))<<endl;
return 0;
}
【解析】
假设编号为 1、2、3 的窗口的办理业务累计的时间分别为 q1,q2,q3,第 i 个客户办理业务的时间为 xi。
对于第 i 个客户,需要找到一个时间结束最早的窗口(即办理业务累计的时间最小的),假设是 qt,那么 qt 加上 xi。
最后 q1,q2,q3 的最小值即为答案。
【题目描述】

每名小朋友只能按照图中箭头指向的方向移动。给出两名小朋友的编号 N 和 M(1≤ N < M ≤ 22),请你找出从编号 N 到编号 M 共有多少条不同的路线。
例如:N = 3,M = 7,从编号 3 的位置到编号 7 的位置共有 5 条路线,分别为:(3->5->7),(3->5->6->7),(3->4->5->7),(3->4->5->6->7),(3->4>6->7)。
【输入格式】
输入两个正整数 N 和 M(1 ≤ N < M ≤ 22),分别表示两名小朋友的编号,之间以一个空格隔开。【输出格式】
输出一个整数,表示从编号 N 到编号 M 共有多少条不同的路线。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n, m;
cin>>n>>m;
n=m-n+1;
int a=1,b=1,c=a+b;
for(int i=2;i<=n;i++)
{
c=a+b;
a=b;
b=c;
}
cout<<a<<endl;
return 0;
}
【解析】
模拟观察可知,从任意位置开始走到后面点的路线其实满足斐波那契数列的特点。
【题目描述】
小明有N(4≤N≤60)个玻璃球,他想将N个玻璃球拆分成若干份(份数≥2,且每份中的数量互不相等),从而使拆分后的每份玻璃球数量的乘积最大。请你编写程序帮助小明计算出最大乘积是多少。
例如:N = 5,5个玻璃球有2种符合条件的拆分方法:(4,1)、(3,2);
其中,能得到最大乘积的拆分方法为(3,2),最大乘积为6(6=3*2)。
【输入格式】
输入一个正整数N(4≤N≤60),表示玻璃球的总数量【输出格式】
输出一个整数,表示最大乘积。
#include<bits/stdc++.h>
using namespace std;
int n, a[30];
int main()
{
cin>>n;
int x=2;
while(x<=n)
{
a[x]=x;
n-=x;
x++;
}
if(n==x-1) a[x-1]++;
for(int i=x-1;n>=1&&i>=2;i--)
{
a[i]++;
n--;
}
int ans=1;
for(int i=2;i<x;i++) ans*=a[i];
cout<<ans<<endl;
return 0;
}
【解析】
本题为中/高级组题目。
把一个数拆得尽量多,这样乘出来的数就会大(1 除外)。那么从 2 开始使用连续的自然数拼凑整数n,
假设拆分到整数 i 时,发现如果加上 i 之后会使得结果大于 n,那么此时还剩下 c = n - i*(i+2)/2,和相等的整数之间越接近其乘积越大,那么可以把 c 依次分配给 i-1, i-2,……,2。
例如:
· 若 n = 9,则 9 = 2 + 3 + 4,此时刚好拆分成三个连续的自然数;
· 若 n = 10,则 10 = 2 + 3 + 4 + 1,但是乘 1 不会增大结果,所以将 1 分配给 4,因此 10 = 2 + 3 + 5,此时结果最大;
· 若 n = 11,则 11 = 2 + 3 + 4 + 2,若此时将 2 分配给 4,结果为 2 * 3 * 6 = 36,和相等的整数之间越接近乘积越大,因此将 2 依次分配给3,4,11 = 2 + 4 + 5,此时结果最大 2 * 4 * 5 = 40;
· 若 n = 12,则 12 = 2 + 3 + 4 + 3,将 3 依次分配给 2,3,4, 12 = 3 + 4 + 5,此时结果最大 3 * 4 * 5 = 60;
· 若 n = 13,则 13 = 2 + 3 + 4 + 4,将 4 依次分配给 2,3,4, 还剩余 1 继续分配给 4,即 13 = 3 + 4 + 6,此时结果最大 3 * 4 * 6 = 72。
综上所述,若拆分到整数 i 时剩余 c(c < i),此时,把 c 依次分配给 i-1,i-2,……,2,每项加一,如果 c = i-1,最后还剩余1,将这个 1 分配给 i-1

添加 家长论坛微信


全部 0条评论