数学奥林匹克小丛书--初中卷:三角形的内心

正文
第七章 三角形的四心
接下来介绍内心:
定义
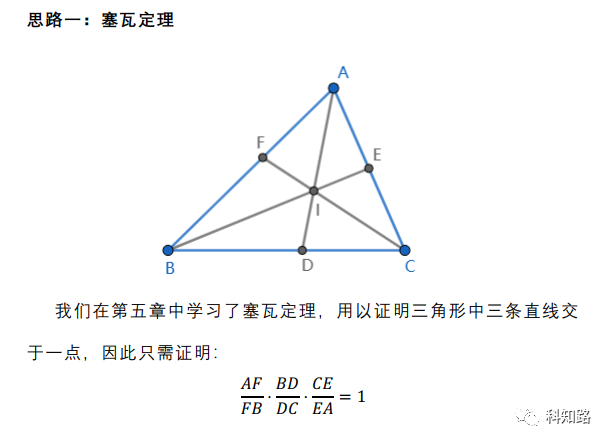
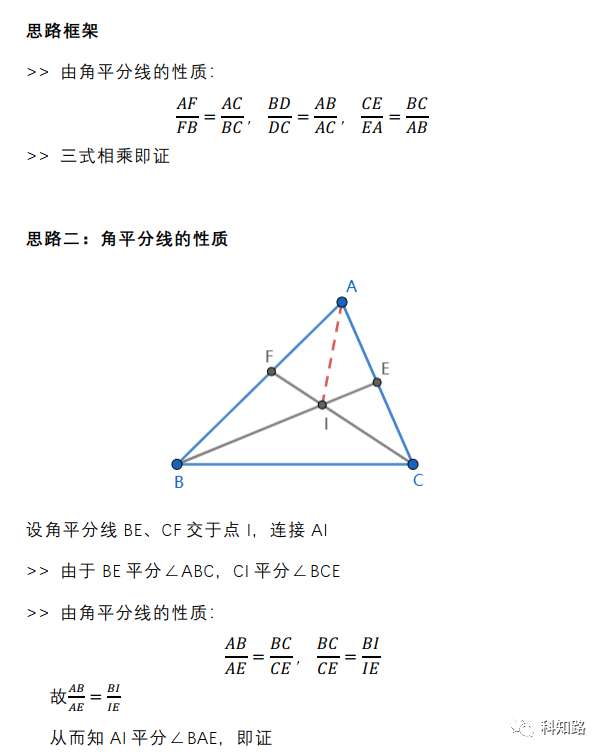
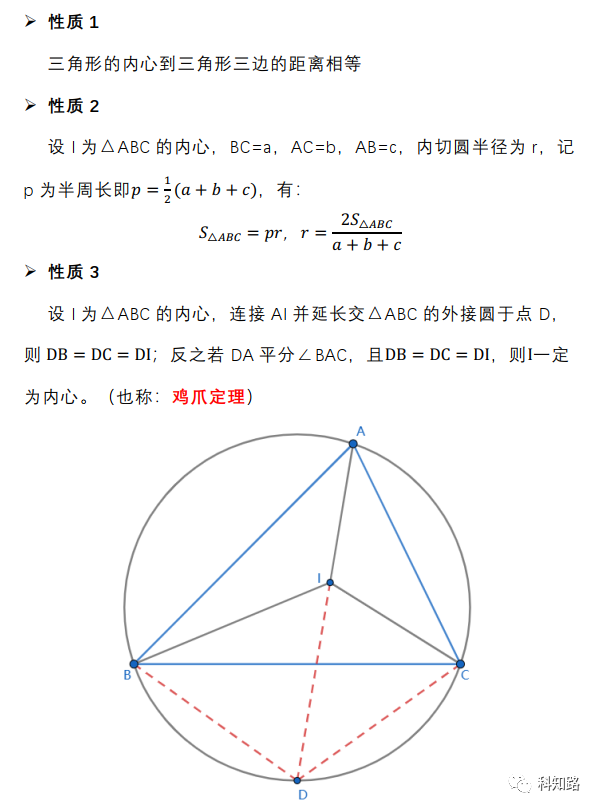
内心作为三角形内切圆的圆心,常常与面积联系起来,接下来看一道例题:
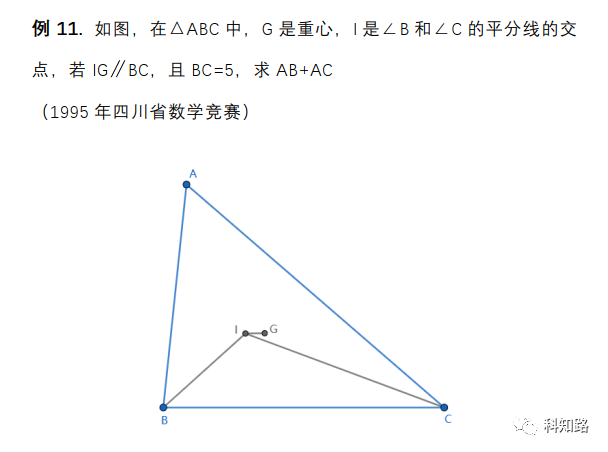
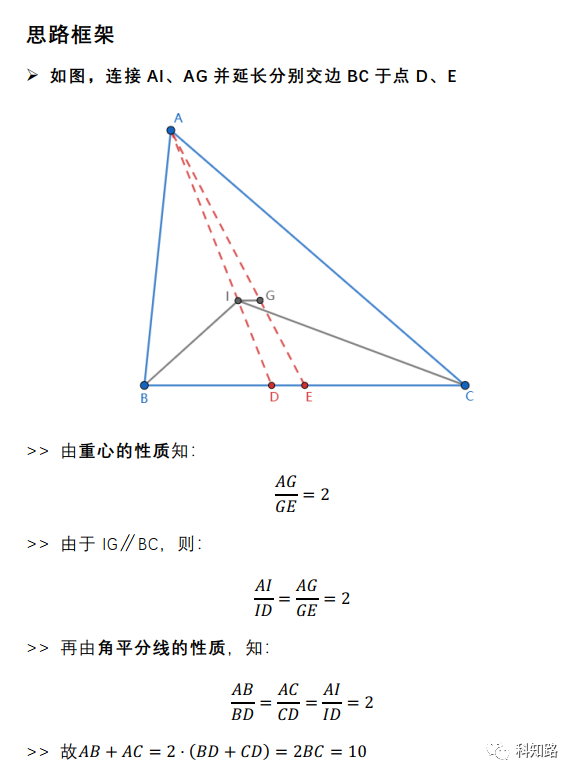


正文
第七章 三角形的四心
接下来介绍内心:


内心作为三角形内切圆的圆心,常常与面积联系起来,接下来看一道例题:





发布于 2024-04-23 10:48
全部 0条评论