世界少年奥林匹克数学竞赛思维能力测评

1
世少赛介绍
作为一项国际赛事,奥林匹克数学竞赛有着悠久的历史和广阔的发展前景。我国从1985年起参加这项赛事并多次取得了优异的成绩。
世界少年奥林匹克数学竞赛(中国区)选拔赛在国内素质教育领域享有极高的口碑,自2006年举办至今有超过三百万人次的学生参与竞赛,其中不乏培养出一批优秀的数学教师和优秀的数学精英。本赛事为世界少年奥林匹克数学竞赛(中国区)选拔赛组委会针对全国青少年的活动。经世界奥林匹克数学竞赛协会研究决定,从"奥数"(07-08赛季)开始,增加了少年级别的国际数学竞赛。也是中国区高中生及大学生多年参加国际奥数竞赛取得优异成绩后在中国举办小学、初中奥林匹克数学选拔赛。
但我们关注的更多是学生的参与,因为数学的学习不是为了取得成绩,是为了让小学生培养逻辑思维能力和空间想象力,以及对抽象思维的提升,为中学期间的数理化学习打下很好基础;培养学生数学自信,拓宽解题思路,激发对理化的兴趣,提高解题能力和理解力。
2
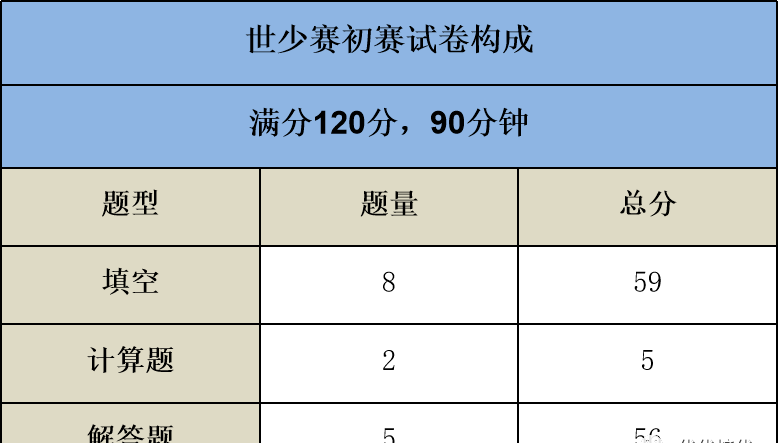
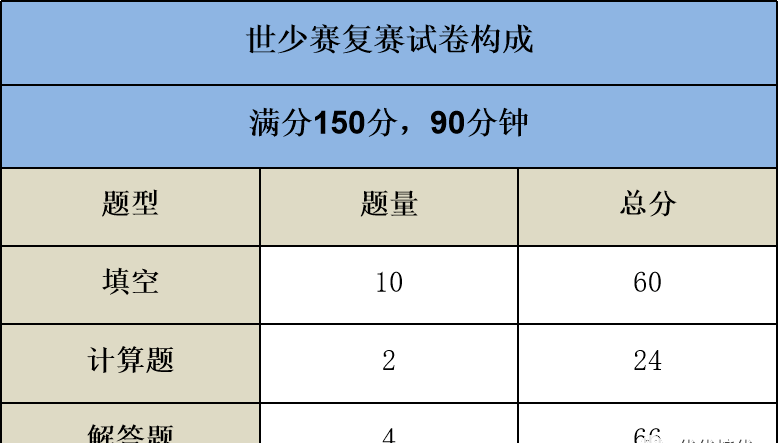
世少赛试卷构成
下表是世少赛各题型占比情况,我们可以看到初赛满分120分的卷子,填空题占59-60分;解答题占56-66分,占比较大。尤其在解答题上,考察的知识点也是相对比较灵活的,所以大家一定要认真备考哦!
计算方面也是需要小朋友们注意,虽然计算题只有两题,但是单题分值很高!
试卷构成
3
二~六年级常考知识点
常
考
二年级世少赛知识点
① 计算:占比15%~20%
计算题大题:考察知识点主要为校内学过的四则运算,添去括号变号,同时也会考察配对凑整以及拆补凑整类型,预测会考察时间计算.代换计算。
② 计数:占比5%-10%
数图形(角、线段、三角形、长方形、正方形等) ,立体图形数图形。
③ 组合
数数中的枚举、生活中的枚举、图形找规律、数列找规律、逻辑推理。
④ 应用题:占比40~50%
乘除法运用、巧移物体、排队问题、和倍问题、间隔问题、还原问题、代换问题,有可能考察数独类型的益智类问题。
常
考
三年级世少赛知识点
① 计算:占比15%~20%
计算题大题:考察知识点主要为校内学过的四则运算,添去括号变号(),同时也会考察配对凑整类型,尤拆补凑整也常碰到,加减的分组法注意也是各别年份常考的类型,偶尔考察乘除巧算与提取公因数计算,稍难部分会出现二次提取的类型。
② 几何:占比15%~20%
平移法求周长是几乎是每年的必考题,可能出现再填空或大题1题,难点在于偶尔考察平移后还有多余的长度需要计算。
③ 应用题:占比65~70%%
平均数问题、和差问题、和倍问题、间隔问题、年龄问题、非整倍问题、还原问题、代换问题,其中比较难理解的是“盈亏问题”,并且逻辑推理、还原常作为大题的最后一题出现,代换问题也通常以文字形式出现,要多读题会分析。
常
考
四年级世少赛知识点
① 计算:占比15%~25%
计算首先固定考察脱式计算两题,是数学考卷的标配。四年级考察的知识点主要为整数的加减乘除巧算,具体就是乘法提取公因数和加减法去括号,针对性的突破训练后难度不大;除此以外,填空题中常出现找规律、定义新运算、等量代换等计算,也都属于中低难度。
② 几何:占比5%~10%
四年级能考察的几何题不多,无非就是长方形正方形的周长和面积以及两个内容综合。其中周长的求法常常用到平移巧算。
③ 应用题:占比65~70%
平均数问题、和差问题、和倍问题、间隔问题、年龄问题、非整倍问题、还原问题、代换问题,其中难度较大的可能是平均数问题,平均数问题考察点一般为“移多补少,需要一定的理解能力。除了以上经典应用题,行程问题也是四年级常见的内容,尤其是火车过桥。
常
考
五年级世少赛知识点
① 计算:占比15%~25%
固定考察脱式计算两题,比于四年级的计算会有一定的难度提升,一是会出现小数,二是会出现大数计算以及椅子数等,方程也是常见的计算类型;除此以外,找规律、定义新运算、等量代换、数字谜等都有可能在填空题中出现,有时候还会结合数论,比如求算式的末位数字。
② 数论:占比5%~10%
所谓的数论,就是因数倍数,质数合数,奇数偶数。五年级常见的数论题型包括分解质因数、找公因公倍数、完全平方数、整除特征等。其中找公倍数结合容斥原理多次出现在大题小题中。
③几何:占比5%~10%
几何题不是固定出现的,有时候基本不考,有时候一下子好几题。考察点也不多,包括长方形的周长巧算,以及不规则图形的面积综合,比如整体减空白等。
④ 应用题:占比60~70%
和差倍问题、年龄问题、非整倍问题、还原问题、植树问题、平均数问题等,其中难度可能较大的是平均数问题,平均数问题考察点一般为“移多补少”,需要一定的理解能力。除此之外,行程问题,折扣问题是新型的应用题型。
常
考
六年级世少赛知识点
① 计算:占比15%~25%
分数巧算:常用方法:通分;约分;裂项
分数比较:常用方法:通分法;接近法;倒数法;相除法,交叉相乘法
归纳推理:常用方法: 观察法;列表格;假设法
② 行程问题:占比5%~10%
a.时钟问题:
整个钟面为360度,上面有12个大格,每个大格为30度;60个小格,每个小格为6度。分针速度:每分钟走1小格,每分钟走6度。时针速度:每分钟走1/12 小格,每分钟走0.5度
b.相遇追及综合:
能够解决行程中复杂的相遇与追及问题能够画出多人相遇和追及的示意图并将问题转化多个简单相遇和追及环节进行解题能够利用柳卡图、比例解决多次相遇和追及问题
c.最值问题:
和一定时,越接近,乘积越大
积一定时,越接近,和越小
d.染色问题
根据奇偶性,画出染色图形
通过实际操作寻找题目中蕴含的数学规律在操作过程中,体会数学规律的并且设计最优的策略和方案熟练掌握通过简单操作、染色、数论等综合知识解决策略问题
③几何:占比5%~10%
圆与扇形周长面积:常用方法:包含与排除;旋转对称,割补平移,公式法
圆柱圆锥:常用方法:表面积公式,体积公式
④ 应用题:占比60~70%
a.分百应用题:单位“1”的寻找、“量”与“率”的对应
b.经济应用题:
售价=成本+利润
售价=成本X(1+利润率)
利润率=利润/成本=(售价-成本)/成本成本=售价/(利润率+1)
定价=成本x(1+期望利润的百分数)
c.浓度应用题:
基本方法:寻找不变量,按基本关系或比例求解,浓度三角(+字交又法)列方程或方程组求解
d.工程应用题
工作总量:一般抽象成单位“1"
工作效率:单位时间内完成的工作量三个基本公式:工作总量=工作效率X工作时间工作效率=工作总量工作时间
工作时间=工作总量工作效率
e.不定方程、方程组解应用题
根据题目叙述找到等量关系列出方程
根据解不定方程方法解方程
找到符合条件的解
f.方程组解应用题
设未知数的主要技巧和手段
找出与其他量的数量关系紧密的关键量用代数法来表示各个量利用“x”表示出所有未知量或变量找准等量关系,构建方程
明显的等量关系与隐含的等量关系)
4
世少赛备考建议
备
考
建议
世少赛中的填空题与应用题部分会有10%-20%的题目在校内知识的基础上展开,所以孩子们不用过于紧张,只要校内知识掌握扎实,一般不会有太大问题的。
其中填空题考察的知识点较明显,运用对应的方法解题即可,可在备考时进行对应题型的专项训练;应用题考察知识点较多,数阵图/幻方/数独/定义新运算等会有一题;图形题会有一题,题目情境不复杂,总体题型比较固定。且填空和应用题的最后一题属于稍有思考量的问题,可以在其他题目确定能拿下的基础上再去挑战。
除此之外,计算的两题几乎是兵家必争之地,属于不能丢分的类型,平时一定要多做计算题,熟练掌握巧算技巧,才能在考试中做的又快又好。




全部 0条评论