第二十三届“YMO”青少年数学思维研学交流活动

复赛试卷

                      小学四年级试题

一、选择题.（把相应答案的序号填在括号里，每题5分，共50分）

1.计算：(2021+2020+2019+2018+2017 )÷5＝（     ）.

A.2017         B.2018         C.2019         D.2020

2.由数字1，2，3，4组成没有重复数字的四位数，所有这些四位数的和是（     ）.

A.666         B.22200         C.6660         D.66660

3.有4个互不相同的自然数,它们的平均数是10.其中最大的数至少是（     ）.

A. 10         B. 11           C. 12           D. 13

4.客车和货车分别从甲.乙两站同时相向开出，第一次相遇在离甲站40千米的地方，相遇后两车仍以原速度继续前进，客车到达乙站、货车到达甲站后均立即返回，结果它们又在离乙站20千米的地方相遇.求甲.乙两站之间的距离为（    ）千米.

A.80         B.90            C.100           D.110

5.有一串数：2，3，5，8，13，21 ，34 ，55 ，89 ……，其中第一个数是 2，第二个数是 3，从第三个数起，每个数恰好是前两个数的和.那么在这串数中，第2019 个数被3 除后所得余数是（     ）.

A.1               B.2            C.0            D.不确定

6.如果从4本不同的语文书、5本不同的数学书、6本不同的外语书中选取2本不同学科的书阅读，那么共有（     ）种不同的选择.

A.30         B.50         C.74         D.120

7.某人骑自行车过一座桥，上桥速度为每小时12千米，下桥速度为每小时24千米.而且上桥与下桥所经过的路程相等，中间也没有停顿.问这个人骑车过这座桥，往返的平均速度是每小时（     ）千米.

A.15         B.16            C.18            D.20

8.定义n!=1×2×3×…×（n-1）×n，求1×1！+2×2！+3×3！+…+2018×2018！+2019×2019！=(     ).

A. 2020！-1      B. 2020！        C. 2020×2020！ D.2021！

9.甲、乙、丙三人都在读同一本故事书，书中有100个故事.已知甲读了85个故事，乙读了70个故事，丙读了62个故事.甲、乙、丙三人都读过的故事最少有（     ）个.

A.15         B.17            C.32            D.62

10.将非0自然数依照下列形式不断写下去：123456……，第2019个数是（     ）.

A.0          B.1             C.2             D.9

二、填空题.（把正确的答案填在横线上，每题5分，共50分）

1.下面的数阵中，第十二行左起第5个数是______.

2.一个学生假期往A、B、C三个城市游览，他今天在这个城市，明天就到另一个城市.假如他第一天在A市，第五天又回到A市.那么他的游览路线共有______种不同的方案.

3.计算1+（1+2）+（1+2+3）+ … … +（1+2+3+…+99+100）=______.

4.如图，把A、B、C、D、E这五个部分用4种不同的颜色着色，且相邻的部分不能使用同一种颜色，不相邻的部分可以使用同一种颜色，那么，这幅图共有______种不同的着色方法.

5.在图中的方格中填入不相同的数，使得每行、每列及每条对角线上的三个数之和都相等，问图中左上角的数是______.

？
		19
	13

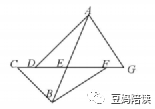
6.如下图，已知CD=5，DE=7，EF=15，FG=6，线段AB将图形分成两部分，左边部分面积是76，右边部分面积是130，那么三角形ADG的面积是______.

7.小明在读一本旧书，读着读着发现有几页丢失了.丢的书页的页码数字最小是143，最大的数是把143的各位数字交换了位置.另外，把丢失的所有页码相加，正好是2000.这本书丢失了______张书页.

8.一个31位的整数，如果把这个整数的每相邻的两个数码组成的整数作为两位数来考虑的话，任何在一个这样的两位数都可以被17或23整除.另外，这个31位数的数码中只有一个7.这个31位数的所有数码之和是______.

9.下图中，四边形ABCD的对角线AC与BD相交于O，E为BC的中点，三角形ABO的面积为45，三角形ADO的面积为18，三角形CDO的面积为69，则三角形AED的面积是______.

10.一个数减去2000是一个平方数，减去2019也是一个平方数，这个数是______.