本讲接着讲解四年级一试11至20题

第11题：

解：从AB×BA=403易知，本题的主要问题为寻找403的因数；

根据数的整除的性质（能被1-12各数整除的数的特性（加更）），可知，1-12都不可以，从13开始试，得：403=13×31，发现13与31刚好符合AB×BA=403，又因为A>B，所以A=3，B=1，则A+2B=5

第12题：

解：由图可知，第一个正方体的火柴数为12根；

前两个正方体的火柴数为(12+8)=20根；

前三个正方体的火柴数为(20+8)=28根；

每加一个正方体，需要加8根火柴，所以，可列出一个，首项为12，公差为8的等差数列：

12，20，28，36……

原题求2017根火柴可以做成多少个正方体，即求最大的第N项，使第N项<2017，根据等差数列的相关公式：

第N项=首项+(N-1)×公差<2017，即：

12+(N-1)×8<2017，解此不等式：

(N-1)×8<2017-12

(N-1)×8<2005

(N-1)<2005÷8

(N-1)<250.125

N<251.125，即N=251

所以，一共可以做成251个正方体。

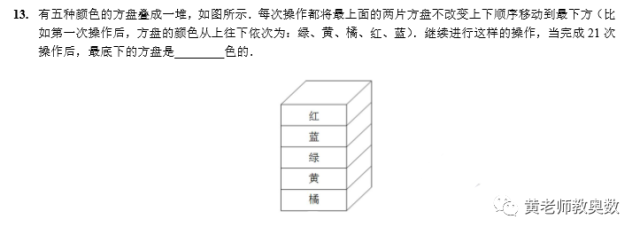
第13题：

解：按照题意操作可知，从第一次操作开始，最底下的方盘颜色依次为蓝、黄、红、绿、橘、蓝、黄、红、 绿、橘……即每 5 次为一个周期。

当完成21次时，21÷5=4……1，相当于完成4个整周期再加一次，即最下方应该是蓝色。

14.小明和小红有如下对话： 

小明说：“我没有超过 40 岁．”

 小红说：“我 38 岁，你至少比我大 5 岁．” 

小明说：“你至少 39 岁．” 

已知这三句都是假话，那么小红________岁．

第14题：

解：

三句话均为假话：

小明说没有超过40岁，即小明超过40岁；

小红说自己38岁，且小明比小红在大5岁，即小红不是38岁，且两人相差小于5岁；

小明说小红至少39岁，即小红没到39岁（且不能为38岁）；

此时可用列举法，小红<39岁，且小红不能为38岁：

当小红37岁时，因小明>40岁，且因为两人相差小于5岁，所以，小明41岁；

当小红36岁时，因小明>40岁，且因为两人相差小于5岁，所以，小明40岁，不合条件；

当小红35岁时，因小明>40岁，且因为两人相差小于5岁，所以，小明39岁，不合条件；

可知，当小红越小时，小明越小，更不可能超过40岁，所以此题只有一个结果，即：小明41岁，小红37岁。

15. 从 1、2、……、1000 中去除所有 2、3、5、7、11、13、17、19 的倍数，将剩下的数中所有合数相加，得到的值为________．

第15题：

解：

剩下的合数不含有因数 2、3、5、7、11、13、17、19，则只能含有因数 23，29，31，37，41，43，47…… 中的一个或几个，原因如下：

4=2×2，因不含有因数2，所以4不在剩下的数中，同理，所有偶数均剩下的数中；

9=3×3，因不含有因数3，所以9不在剩下的数中；

下同，略；

所以从最小的23开始乘起，经有序枚举可知：

23×23=529 、23×29=667、23×31=713  、23×37=851 、23×41=943 、 23×43=989(23×47>1000，故不再考虑) 、29×29=841 、29×31=899 (29×37>1000，故不再考虑) 、31×31=961

求此9个乘积的和为7393。

第16题：

解：图中每条边上都有五个小正方形，所以每条边上有1+2+3+4+5=15个长方形，所以四条边上共有 15×4-4=56个长方形(每个角上的小正方形均被数了两次，故要减掉4)；

除了阴影部分，内部还有 5 个小正方形；

此外，每个角上的田字格中， 还有 2 个1×2 的长方形和 1 个2×2 的长方形未被计算，所以还有4×(1+2)=12个；

故一共有56+5+12=73 个不同的长方形。

17. 在一个边长为 7 厘米的正方形上，剪掉边长分别为 1 厘米、2 厘米、3 厘米、4 厘米的小正方形，那么剩余图形的周长最小是________厘米．

第17题：

解：求周长最小，即使减后的图形凹凸尽量少，答案见下图：

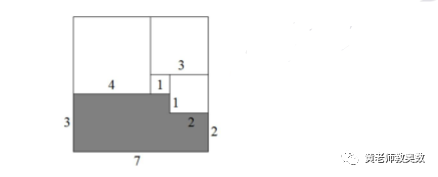
上图中，白色部分为剪掉部分，阴影部分为剩余部分。

剩余图形的周长最小为 20厘米．

注：可以补成一个长为7、宽为3的长方形计算周长；也可以每段长度加起来。

18. 99×n 的值的各位数码要么是 1，要么是 2．满足要求的正整数 n 最小为________．

第18题：

解：为讲解方便，令A= 99×n；

当 n 最小时，A要尽量小；

因为A= 99×n，则A 是由 1 和 2 组成的 99 的最小倍数

根据能被99整除的数的判定标准，即用“两位截断法”。两位截断法，就是两位一分隔，然后求和，和能被99整除，这个数就能被99整除。在上一讲中环杯五年级第七题有详细讲解(2017年中环杯初赛 五年级试题讲解（前十题）)；

由于 99 的整除特征为两位截段后每段数的和为 99 的倍数，把99分拆，要求位数尽量小，且只能出现1、2两个数字：

99=22+22+22+22+11

则A=1122222222时最小，所以n=A÷99=11335578

19. 现在有一串用字母 X 和字母 O 构成的字符串，接下来可以进行下面这些操作（每次操作都是选择其中的一 种）： 

将某一个字母 X 替换为 XO． 

将某一段字母串 XXX 替换为 OX． 

将某一段字母串 OO 替换为 XOO． 

最少要操作________次，才能将字符串 OOX 变换为 OXOOOX．

第19题：

解：仔细观察最终的变换结果“ OXOOOX”，发现开头的两个字母为“ OX“，而“ OX“只能为”XXX"变换得出；故前三位需要变换成”XXX"；

一：OOX 变为 XOOX(前面两个“O”变换)

二： XOOX 变为 XXOOX (中间两个“O”变换)

三：XXOOX 变为 XXXOOX (中间两个“O”变换)

四：XXXOOX 变为 XXXOOOX (难点：此处需要把第三个"X"换成“”XO")

五：XXXOOOX 变为 OXOOOX．

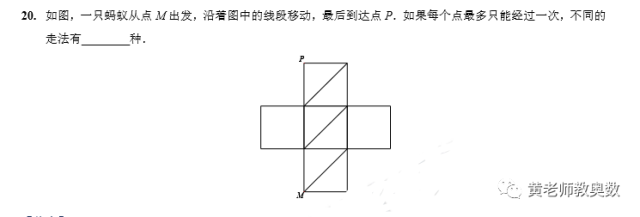
第20题：

解：此题注意，没有最短距离之类的要求，仅要求每个点多只能经过一次。

为讲解方便，在原图上标上各点字母：

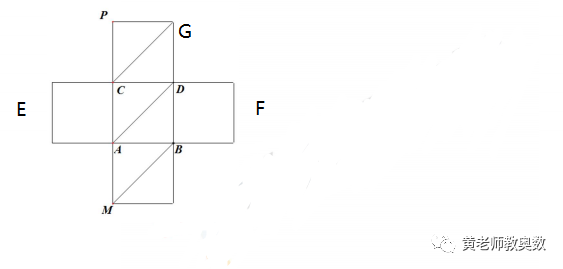
通过有序列举法来解：

本题中，从M点出发，只有两种选择，一种是到A点，一种是到B点，而到B点又有两种选择……

黄老师以M点出发直接到A点为例，把有序列举讲一下，详见下图：

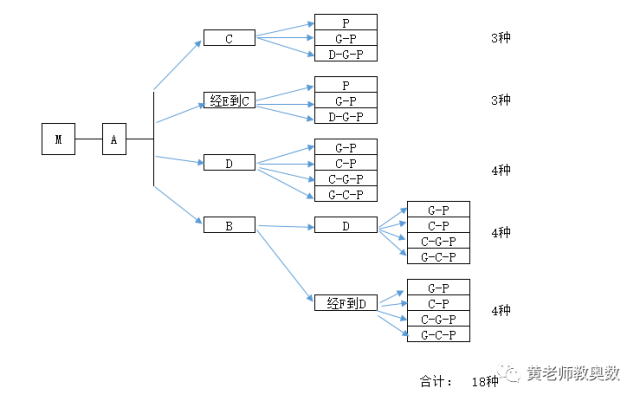
故M出后发直接到A点有18种不同的线路。

经M出后发直接到B点有2种选择，B到下一个点亦有3种选择，请朋友们自行做答

本题最终的答案为70种。

---

添加 家长论坛微信