第十五届中环杯数学竞赛初赛三年级考题

1. 计算：3x995+4X996+5X997+6X998+7x999-4985x3

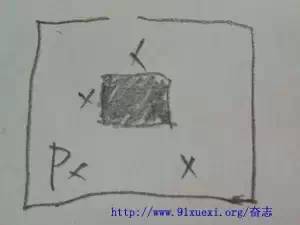
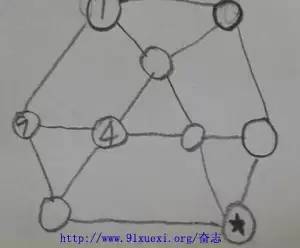
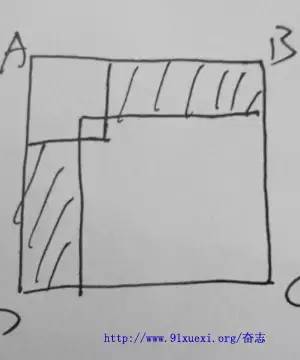
2. 一个数除以20的商是10，余数是10，这个数为

3. 如图是一个美术馆的俯视图，每个“X”表示A、B、C、D四人中的一个人，在美术馆中央是一根大石柱。已知A看不到任何人，B只能看到C，C既可以看到B也可以看到D，D只能揽到C.那么，？在P点（填A、B、C或D）

4. 甲、乙两人相约去餐厅吃饭，由于这家餐厅圣体火爆，所以加到了以后先拿到一个等位号码，顺便等乙。乙过了一会儿也到达餐厅，但是他没看到甲，所以也去拿了一个等位号码。等位的时候乙看到了甲，两人拿出了等位号码，发信这来那个号码的数码是顺序相反的两位数，而且两个号码的数码和（比如：数字23的号码和为2+3=5）都是8，而乙的号码比甲大18.则甲的号码为__________

5. 将1-9这9个数分别填入图中的圆圈内，使得每个三角形（共7个）的3个顶点上的数之和都等于15.现在已经填好了其中的3个，则标有“★”的圆圈内应填_________

6.10个学生（其中一个是队长，9个是队员）组队参加数学比赛，结果拿了第一名。组委会决定颁发给队员每人200元奖金，队长比全队10名选手所获得的平均奖金还多90元。则队长所获得的奖金为多少元？

7.森林里的小动物们外出郊游，他们排成了一列长40米的队伍，以每秒钟3米的速度前进，小兔子有事要从排尾赶到排头并立即返回排尾。小兔子的速度为每秒5米，那么经过多少秒，小兔子可以返回排尾。

8．将4*4的大正方形切割为16个1*1的小正方形，擦去期中的两条线段，得到如图所示图形，则图中一共有多少正方形？


9.用三个长方形拼出一个大长方形（没有空隙，没有重叠），其中的两个长方形分别为75px*200px和50px*125px，那么第三个长方形的尺寸有几种？

10.一个人去丛林打猎，发现一群狼，这群狼里面夹杂着一些变异狼，已知这个人有一个头两条腿，普通狼有一个头四条腿，变异狼有两个头三条腿，所有人和狼加起来有21个头57条腿，则所有狼（包括变异狼）有几头？

11. 如图，从A走到B，每次走一格，只能向下或者向右走。将一路上的数字全部加起来（如果走到黑格，就直接加5），最后的总和为51.不同的走法有几种？

12. 把从1开始的连续自然数写成一个数串：1357911131517。。。，一直写到这个数串第一次出现“2014”为止，共写了几个数字？

13. 如图，将从1开始的自然数按照一定的规律排列起来，那么第3行第51列的数是？

14. 如图，相同的汉字代表相同的数字，不同的汉字代表不同的数字。所有的汉字都不为0，也不与图中已经出现的数字相同，那么四位数“中环杯棒”=？


15. 如图，正方形abcd的面积是196平方厘米，它包含了两个有部分重叠的小正方形。其中，较大的那个小正方形面积是较小的那个小正方形面积的4倍，而且两个正方形的重叠部分面积为1平方厘米。那么阴影部分面积为？

16. 将1-6填入右图的三个算式中，每个数恰好使用一次，使得A+B是2的倍数，C+D是3的倍数，E+F是5的倍数，则C、D中的较小的数为？

17. 从边长为20的正方形中去掉一个面积为36的长方形，这个长方形的两条边长都是整数，并且长方形的一条边长是正方形某条边长的一部分。剩下图形周长的最大值是？

18. 四辆车同时进入一个圆形跑道，每辆车的行驶路线如图所示，所有车都是顺时针行驶。每辆车在开满一圈前都要离开这个圆形跑道，任两辆车选择的出口均不同。那么，有几种不同离开跑道的方法。

19． 如何，将1-6这六个数字填入图中的圆圈内，使得每一个圆圈内的数字等于其下面相邻两个圆圈内的数字之差，当然，最下面三个圆圈内的数字不用遵从这个规定。那么最上面的那个圆圈内的数字是？

20. 如下图，左面这个图形可以由三块相同的图形拼成。则这三块相同的图形可以使下列选项中的？