2022年AMC12B中的小奥题解答与

AMC的简单介绍
AMC的A代表America,即美国。
我们都知道小学阶段有个数学活动叫“美国大联盟”,AMC则是美国在初中阶段的数学活动,分三个等级AMC8、10和12、数字对应年级,即推荐8(初二)、10(高一)、12(高三)年级的孩子参加。
理论上地位应该对标咱们的初高中数学联赛,然而题目的难度实在是不够看的,高联一试的难度吊打AMC12几条街。
不过AMC12成绩的全球前5%会有资格参加下一阶段的AiME,这个阶段的试题难度就接近或略高于咱们的高联一试了,这才是正餐,AMC就是个海选。
所以国内孩子参加的话,完全可以提前2~3个年级报名参与。
比较特殊的是,AMC10和AMC12中都有30%~50%的篇幅在考小奥。其实原因也简单,毕竟现今小奥的大部分专题都是高中竞赛知识点简单化、弱化之后下沉到小学的。然后美国人考的又简单,所以最后整个试题就都变成小奥题了,笑。
小学生做这些题的话,最大的障碍应该就是语言了。这里的语言分两种:
1、看不懂英文。这里指的主要是一些专业的数学术语和逻辑结构。不过从去年开始,中国地区的AMC开始提供官方翻译,很大程度的解决了这一问题,但翻译质量比较堪忧,今年就有好几道题,看英文非常好懂,看中文非常拗口,感觉像是机翻。
2、看不懂数学语言。很多题目以集合、命题、区间、函数这些数学化、符号化的语言诠释,小学生没有接触过,不明白题目表示的意思,这个就没太好的办法了。
而这些小学生能做的题目,主要集中在数论、计数、几何这三大板块上。如果学过根式的计算,那么应该可以解决所有的几何题,没学过根式的话稍微有些受限,但大部分题至少也属于会做不会算的程度。
小奥部分试题简评
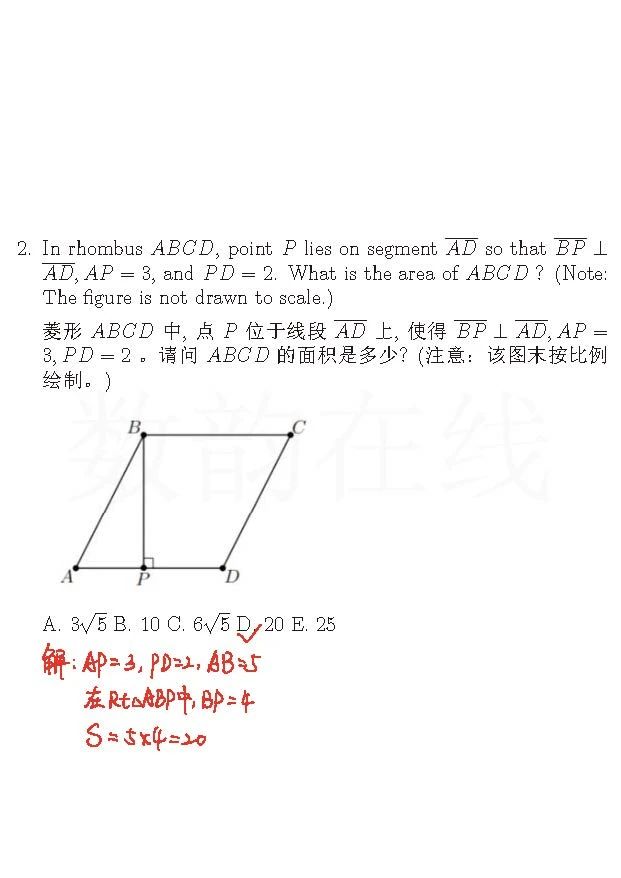
第2题,比较弱智的一个勾股定理,四年级难度。(题外话,我做的是纯英文题面,不认识菱形这个词,然后读完题就知道这个词只可能是菱形。所以数学题,不认识单词真的不重要。)

第3题,特殊结构多位数的拆分,也是高思导引四年级《多位数与小数》那一讲的内容,不过题目比导引上的题还是难一些的,倒是跟导引那一讲的超越7特别像——不过那个超越7小学生本来就不可能做出来,跟这个倒是卧龙凤雏。

第4题,小学生大概做不了,因为用一元二次方程包装了一下,但本质上还是个小学数论问题:两个自然数的平方差为4×36,这两个数有多少种不同的可能?当然这里因为有负数,所以解的个数翻倍了,仅此而已。
平方差的拆分,对应高思导引六年级《数论综合二》这一讲,难度跟上面的拓展篇差不多。

第6题,余数计算,读懂题意的话还是比较好思考的,只要能意识到连续10个数中,第一个数除以7的余数决定了后续数中有几个7的倍数,这个题就能做出来。

第7题,列方程解应用题+最值判断。小学课内讲统计的时候,不知道现在还有没有“众数”这个概念,平均数跟中位数是有的,如果学过的话这题很简单,四年级难度。

第12题,古典概形计算。这道题是有一定难度的,小学生有能力做,但不好做对。难点在于正着求概率基本是没法正确求出的,因为重复情况太多了,一定要反求。而反求的话有两种不同的错误情况,得分开考虑,同样要避免重复。
正难则反和规避重复是计数题中很重要的两板斧,要熟练掌握才好。

第13题,第二道勾股定理。比2难在多了一步相似,不过直角三角形的相似默认孩子会,国内近几年的小学数学活动基本已经把这个作为默认掌握的知识了,所以小学生做应该也没啥难度。

第15题,乘方的余数判定,只要能意识到用余数来判断整除性就好做。整除相当于余数为0,这是数论出稍难一些题时会用到的。
本来乘方的余数要用费小或者欧拉,但这题底数是2,模是3、5、7,数太小了,枚举就能枚举出来,杀鸡焉用牛刀。

17题,用小学生习惯的表达翻译一下题目:
将10枚棋子放入4×4的棋盘中,每个格子最多放1枚棋子,让四行中的棋子数分别为1、2、3、4枚;四列中的棋子数也分别为1、2、3、4枚,有多少种不同的方法?
排列组合里一个特别经典的问题,就不多说了。

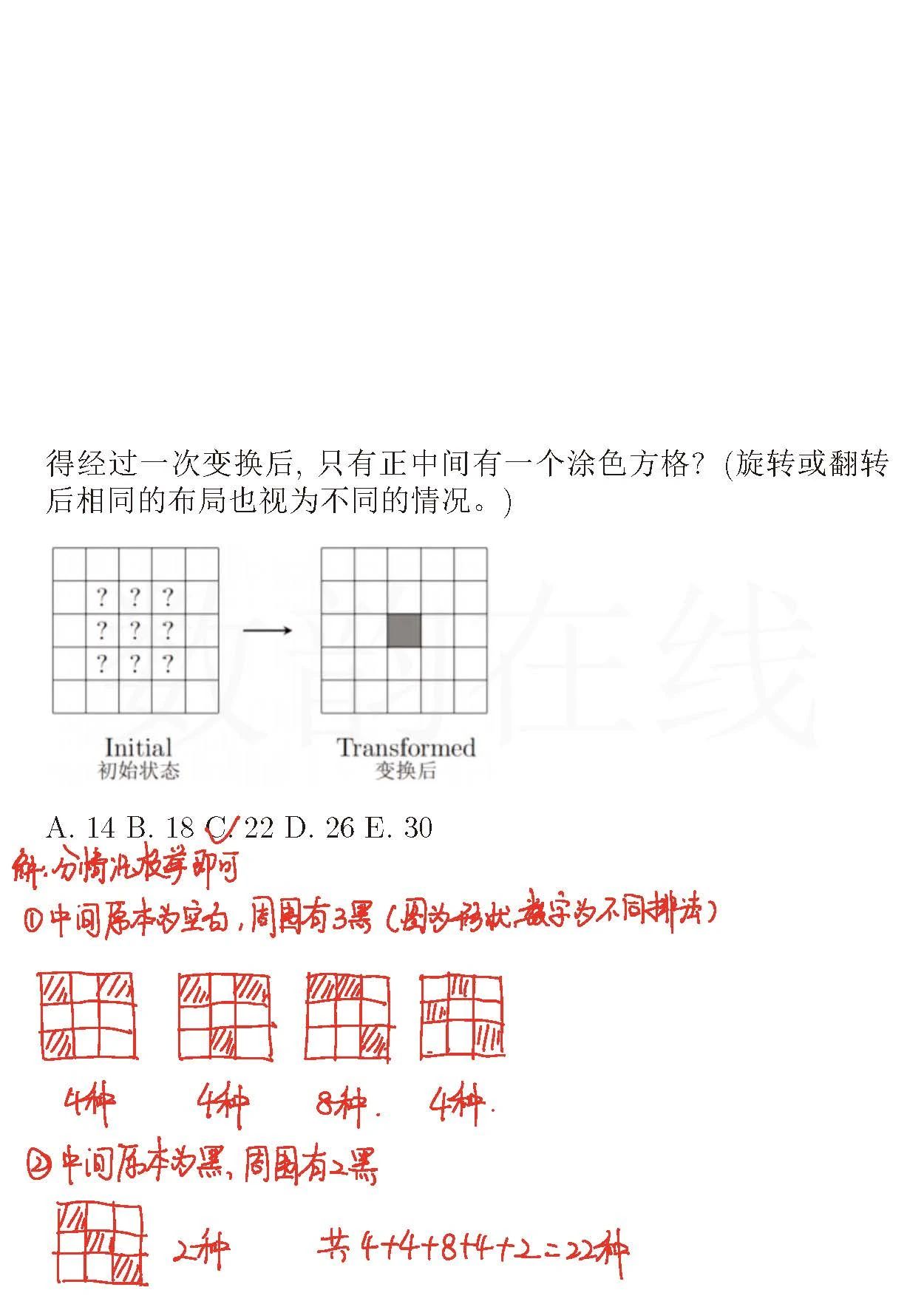
18题,中文翻译太烂了,反而让人看不懂,就不贴中文翻译了,这个难度的英文大家应该也能看得懂。
本质上是个分类枚举计数,属于小学生有能力做,但高中生也很难做对的问题。需要分类讨论的情况还是比较多的。
我自己的做法是按照中间块为黑或白分两大类,再看周边8个格子中角块和棱块的个数(3角0棱,2角1棱etc)。解析写着看起来很简单,真正拿来讲的话估计要10分钟左右才能讲明白,且题里面有坑——某些看起来合理的排列会让周围的白格变黑从而出现矛盾。
这题强烈建议所有人都动笔试一下。

22题,几何概形就不那么小学了,不过去年ZP就考了两道几何概形,所以还是放过来。
当然这题在几何概形里也算是个难题了,理解题意找到对应模型本身就不容易,还要意识到需要分两类情况进行讨论。最后就是第一种情况涉及到三维坐标系中的几何概形分析,不好想到。
很难的题,但很有意思。建议有能力的孩子挑战一下。

23题,二进制。其实我自己做这个题的时候没用到二进制数,做完了想想发现用二进制更简单,列个竖式就什么都看出来了。
当然竖式法做这个题的难点在于要意识到模2^n余1的数的二进制表达特征式,孩子可能不太好想到。
还有一个比较坑的一点是,虽然后面每个数位都以3为周期,但x3不等于x0,这个还挺容易错的。
聊聊小奥的普适性
在高中数学活动中见到高比例的小奥试题,可能很多家长觉得有点匪夷所思,但其实还挺正常的。
相较于课内数学而言,小奥学习的本身就是数学思维,而思维既无国界之别,也无年级之分。
除了上面提到的高中数学活动,其实初高中的物理、化学学习中,小奥的知识都能在不同知识点上起到极大的帮助,比如运动物体分析、浓度混合、氧化还原方程式配平等等。
另外,我个人体会最深的一件事是,最近我在备考MBA的笔试,里面有一门课叫《管理学综合》,总共130分的客观题,考的全是数学。其中小奥有15题,初高中数学有10题,还有40道被称为“逻辑题”的部分,本质也和数学息息相关。
当我10月份第一次翻开真题,想知道笔试究竟考什么的时候,突然就觉得“这把稳了”,笑。
而这种考试既然会考小奥,也从侧面说明了小奥的意义。
所以小奥的意义,远远不只是几张活动证书那么简单。
一个小彩蛋
上面提到过,MBA笔试统考的《管理学综合》《经济学综合》里面,同样充斥着大量的小奥内容。
所以后面我估计会在B站开一个专栏,按小奥专题整理近十年的管综真题,并从一个专业的小奥老师角度做一个梳理串讲。
如果有跟我一样在备考MBA的家长,可以用作参考。
不过更多的意义在于,对于咱们的孩子,也可以看看另一个视角的“小奥题”,欣赏一下同一知识点的不同风景。

添加 家长论坛微信



全部 0条评论