美国大联盟杯赛备考指南

part1:杯赛介绍

3 - 11年级美国、加拿大、中国的学生
活动日期和时间:
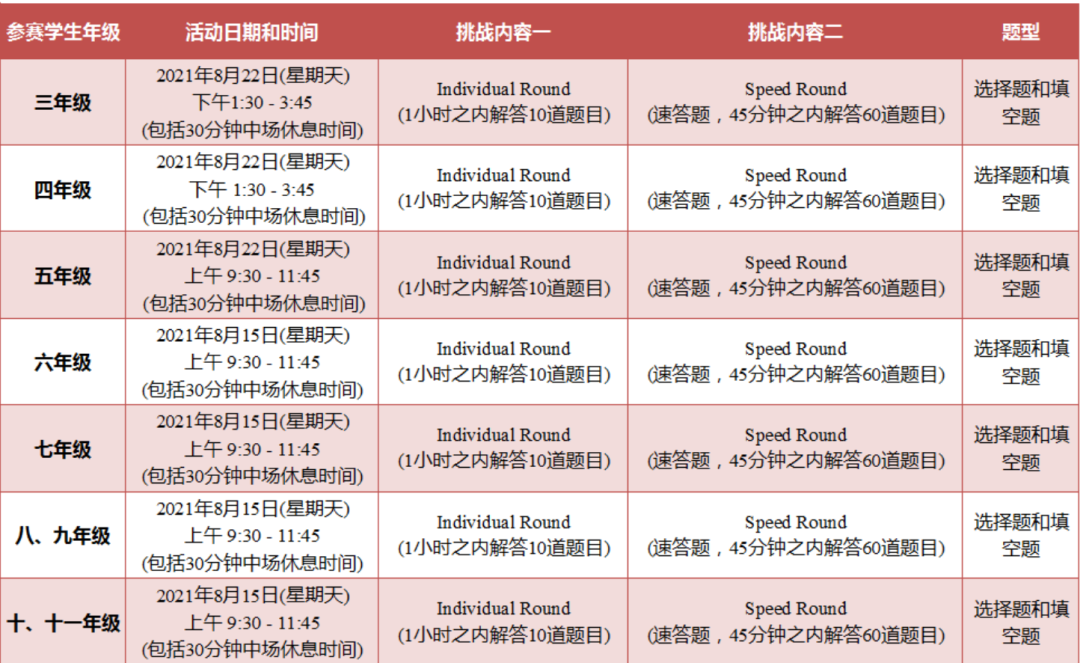
6 - 11 年级学生: 2021年8月15日(星期天)上午 9:30 - 11:45 (在线, 其中10:30 - 11:00 为30分钟中场休息时间)
5 年级学生: 2021年8月22日(星期天)上午 9:30 - 11:45 (在线, 其中10:30 - 11:00 为30分钟中场休息时间)
3 - 4 年级学生: 2021年8月22日(星期天)下午 1:30 - 3:45 (在线, 其中2:30 - 3:00 为30分钟中场休息时间)每个年级的挑战活动分为Individual Round (个人赛)和Speed Round (速度赛)。
全英文试卷。3-7年级每个年级分别一套试卷,8-9年级同一套试卷,10-11年级同一套试卷。
考试期间学生可以使用组委会提供的英汉数学词汇手册(在线)。
考试期间禁止使用任何其他字典、词典、计算器、及任何资料(包括纸质及电子版的)。
2021美国"大联盟"(Math League)国际夏季数学挑战活动每个年级设置以下奖项(8-9年级学生一起评奖,10-11年级学生一起评奖):
Gold Medal (国际金奖): Top 5%
Silver Medal (国际银奖): Top 15%
Bronze Medal (国际铜奖): Top 30%
Proficiency Award (中国赛区优胜奖): 各赛区(省、直辖市)除国际奖项之外前20%
Individual Round (个人赛) 和 Speed Round (速度赛) 分别评奖。
其他参赛学生获得Certificate of Participation证书。

在大联盟活动中,数论模块考的比较多的就是“因倍质合”、“整除与余数”等,且题目本身难度不大,解决数论题目的关键仍然在于读懂题目,其中的关键字眼对于整道题的理解非常重要,反过来当你遇到特定的英文单词时,就能猜测此题考查的是数论模块,继而用自己熟练的数论知识解题即可。

我们先来看看在题目常见的“数”:
factor(因数)、
multiple(倍数)、
prime number(质数)、
composite number(合数)、
integer(整数)、
natural number(自然数)、
remainder(余数)、
common factor(公因数)、
common multiple(公倍数)等。
看到这些单词,很大程度上在考查数论部分的知识点。
单词——数

词组与搭配

单词——杂

不需要执着把每个单词拼写背下来,只要混个脸熟,知道意思就行。

真题演练1
The greatest of common factor of two number is 3. The product of these two numbers must be divisible by
A)6 B)9 C)12 D)18
此题中标红的是关键字,这三个短语都在上面的词汇出现过:
the greatest common factor 最大公因数
the product of 某数之积
be divisible by 可被某数整除
从短语意思入手,明显提示考察数论中的因倍质合与整除,整题大意为“两数的最大公因数为3,那么这两数的乘积一定能被xx数整除”,两个数都含有因数3,那么乘积一定会含有因数3×3=9,因此两数的乘积一定能被9整除,故本题选B。
真题演练2
Of the following, which is the sum of two consecutive integers?
A)111111 B)22222
C)444444 D)888888
此题中标红的是关键字,the sum of在很多英文数学题都很常见(不仅在数轮题),意味求和,最关键为后面这个短语
“consecutive integer 连续的整数”,整题大意为“以下的数中,哪个会是连续的两个整数的和”,题目读懂后发现这是一道极为简单的关于奇偶性的数论题,连续两个自然数/整数,为一奇一偶,其和一定为奇数,故此题不用计算,除A选项为奇数外其余均为偶数,故本题选A。
真题演练3
On each of the four shelves of my bookcase is a different prime number of books. There could be a total of ________bookson my shelves.
A)15 B)21 C)22 D)24
此题中标红的是关键字,最关键为后面这个短语“adifferent prime number不同的质数”,再加上前面“four shelves”限定为4个。整体题意为“我的四个书架上书本的数量分别为4个不同的质数,那么书架上书的总数有可能为多少本”,换而言之,就是求4个不同质数的和的可能性有哪些。
此题考察100以内的质数,20以内应该能脱口而出(2、3、5、7、11、13、17、19),因为本题给出的选项的数不大,通过简单枚举,只有21=2+3+5+11符合题意,故本题选B。
真题演练4
For how many differentpairs of unequal positive integers lessthan 10 is the least common multiple of the numbers less than their product?
A)6 B)7 C)8 D)9
此题有两个难点,一个是短语的理解(解题关键),一个是数学题目本身有难点和易错点。“different pairs of unequal positive integers”不同的正整数对,“the least commonmultiple of the numbers”最小公倍数,整体大意为“有多少对小于10的不同正整数对,使得它们的最小公倍数小于它们的乘积”;理解题意后,本题讨论数的范围不大(1-9的整数),要清楚什么情况下两数的最小公倍数会小于两数的乘积,也就是要两数不互质,通过枚举可得(容易漏,建议有序枚举),(2--4/6/8)3个,(3--6/9)2个,(4--6/8)2个,(6--8/9)2个,共3+2+2+2=9个,故本题选D。

做大联盟数论题,要学会从关键的英文单词中获取考点信息,借助扎实的数学功底和对应的知识点去理解题目大意,数论题目在大联盟当中考查的数学本身难度不大,建议大家要熟悉相关的单词短语。

添加 家长论坛微信



全部 0条评论