2022年超常【数学】思维竞赛（五年级试题）

考试时间：100分钟 满分：150分

考试说明：

（1）本试卷包括30道不定项选择题（可能有几个选项正确），每小题5分.

（2）每道题的分值按正确选项的个数平均分配，但是如有错选，则该题不得分.

1.本题是由许多木块图形，从不同的方向转动所形成的，从下方的五块木块中选择一块和最上方的木块完全相同，只不过是被转到不同的方向，从不同的角度来看罢了.（ ）

2.任取一个能被9整除的2022位的数，它的各位数字之和记为𝑎，𝑎的各位数字之和记为𝑏，𝑏的各位数字之和记为𝑐.则𝑐=（ ）.

A.9 B.6 C.3 D.18 E.以上都不对

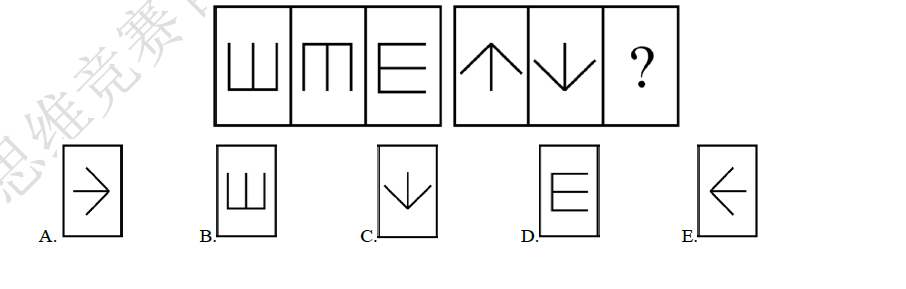
3.从所给五个选项中，选择最合适的一个填入问号处，使之呈现一定的规律性. （ ）

4.把37分拆成若干个不同的质数之和，共有（ ）种不同的拆法，将每一种拆法中拆出的质数相乘，乘积最小为（ ）.

A.9,288 B.10,288 C.11,435 D.12,588 E.以上都不对

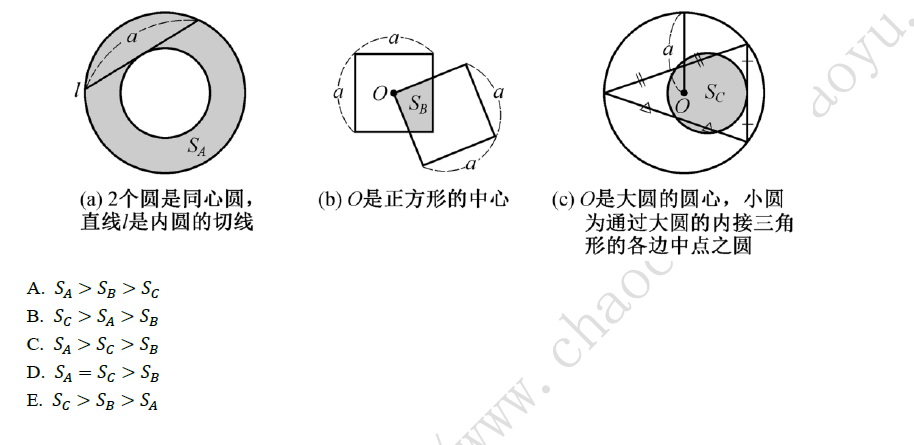
5.能正确表示图（a），（b），（c），中阴影部分面积𝑆𝐴，𝑆𝐵，𝑆𝐶的大小关系的是（ ）.

（图中长度单位为cm）

6.四位数𝑎𝑏𝑐𝑑，𝑑𝑎𝑏𝑐，cdab，bc𝑑𝑎分别是5，9，11，和23的倍数，则𝑎𝑏𝑐𝑑=（ ）.

A.2385 B.4455 C.6075 D.7155 E.以上都不对

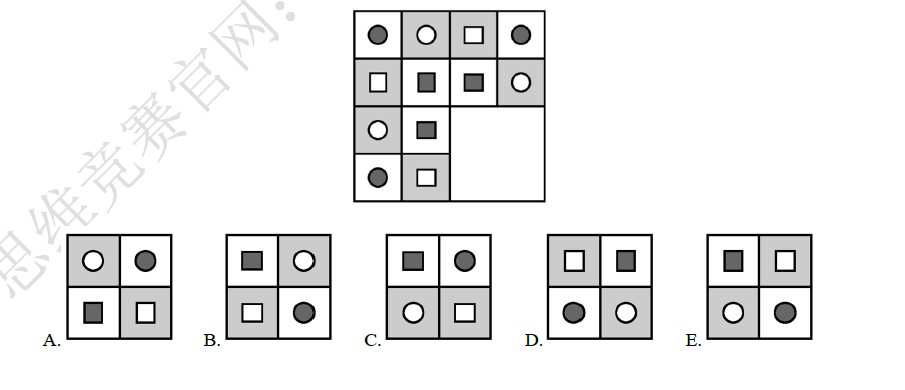
7.上方有一个大正方格，内有三个图面和一个空栏，请你首先观察出三个图面的矩阵排列关系，然后从下方五个选项中找出正确的图面来.（ ）

8.下题图形中，正方形有（ ）个

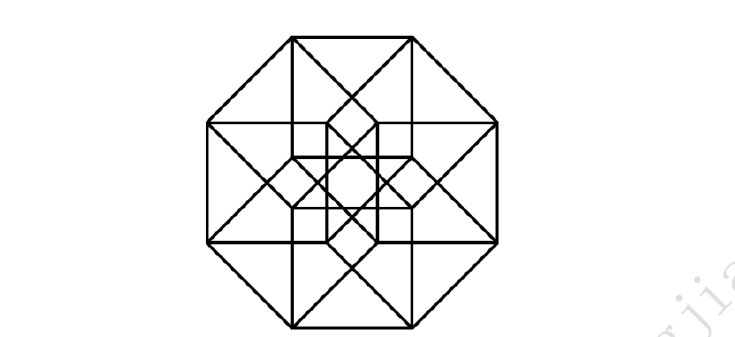
A.18 B.17 C.16 D.20 E.以上都不对

9.三人买了10个面包，平均分着吃.已知甲付了6个面包的钱，乙付了4个面包的钱，丙没带钱.吃完他们算了一下账，丙应该付出的钱，要按（ ）分给甲乙二人才合理.

A.6:4 B.4:1 C.3:1 D.2:1 E.以上都不对

10.在下图中，每一个正三角形的边长都是中间那个正六边形边长的两倍. 请问正六边形的面积占正六边形与六个正三角形面积总和的（ ）.

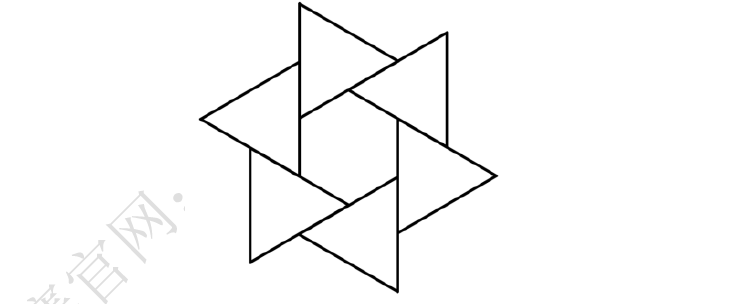
A. 16 B. 112 C. 34 D. 14 E. 15

11.如图，△𝐴𝐵𝐶是边长为108cm的等边三角形，虫子甲和乙分别从点𝐴和点𝐶同时出发，沿△𝐴𝐵𝐶的边爬行.甲顺时针爬行，乙逆时针爬行，速度比是4:5.相遇后，甲在相遇点休息10 s，然后继续以原来的速度沿原方向爬行；乙不休息，速度提高20%，仍沿原方向爬行，第二次恰好在𝐵𝐶的中点相遇.则开始时，虫子甲的爬行速度为（ ）cm/s.

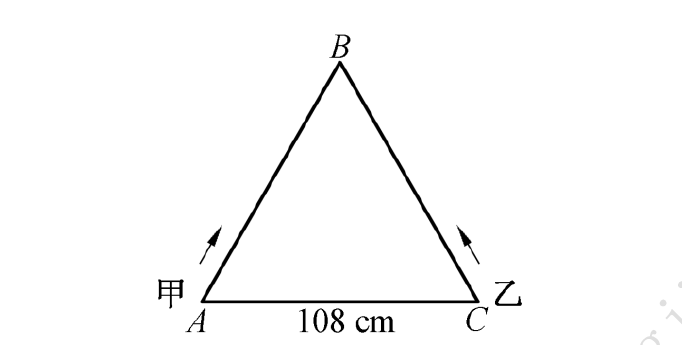
A.8.6 B.9.6 C.10.6 D.11.6 E.15.9

12.根据图中给出的数据，𝑎+𝑏=（ ）.

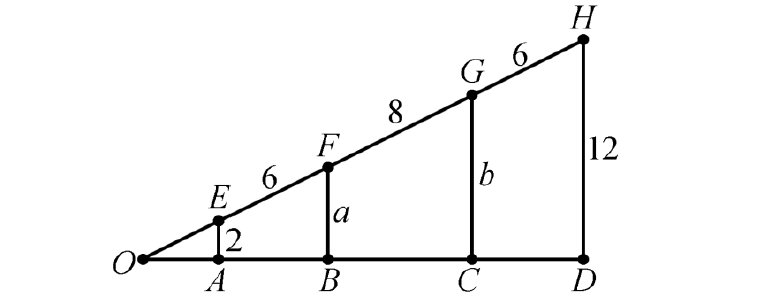
A.10 B.14 C.16 D.18 E.以上都不对

13.

上表中，将每列上下两个字组成一组，例如第一组为（共，社），第二组为（产，会），那么，第100组是（ ），第2022组是（ ）.

A.(共，社) B.(好，好) C.(产，会) D.(好，义) E.(共，义)

14.把1至10共十个正整数平均分为两组，每组五个数，使得第一组数的乘积可被第二组数的乘积整除，则商的最小值是（ ），如果还要求商是奇数，那么商的最大值是（ ）.

A.6,169 B.7,165 C.7,175 D.8,188 E.以上都不对

15.如图，这是一张5行5列的方格表，顶上一行填有符号𝑃，𝑄，𝑅，𝑆，𝑇，第四行中间填有符号𝑃，𝑄，𝑅，余下的方格中可填入𝑃，𝑄，𝑅，𝑆，𝑇，要求做到同一符号在每一行、每一列、及每条对角线上只出现一次.那么填入画有阴影的方格中的符号必须是（ ）.

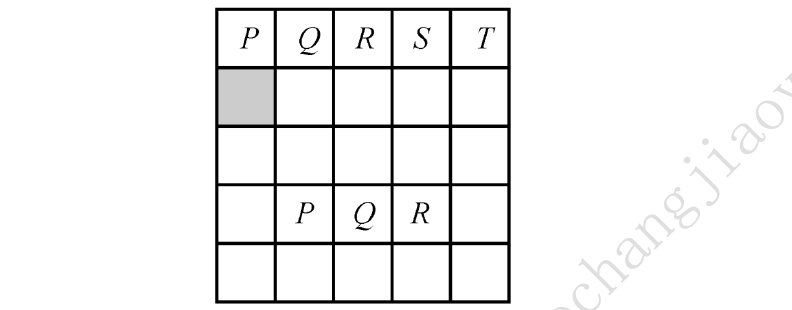
A.P B.Q C.R D.S E.T

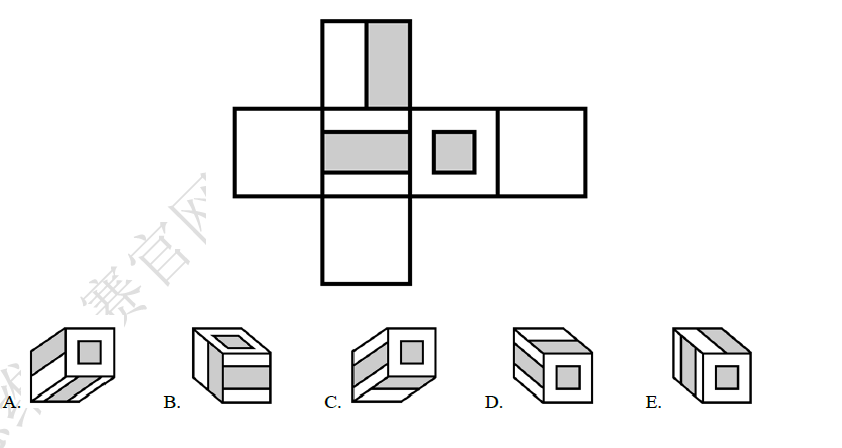
16.立体组合与展开是一体的两面，只要了解组合之规则，同样可以施用于展开，反之亦然.不论是组合还是展开，都有三面图案，三者之间均有相对位置、方向性等关系.只要固定一图案，将其他两个图案与其比较相互之间的关系，即可找到正确的组合或展开图.上方图形是下列哪个立方体的展开面? （ ）

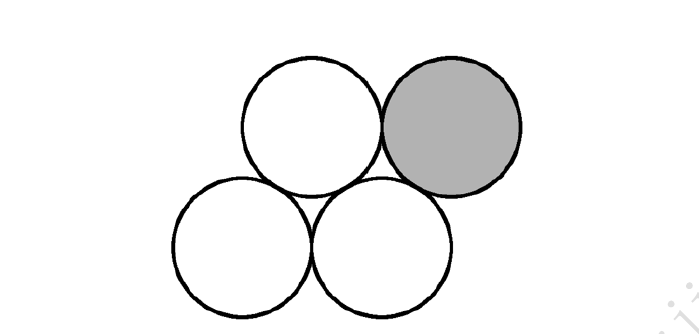
17.如图，将四枚硬币放置于桌面上，把有阴影的那枚硬币紧贴另三枚硬币的圆周转动，最后回到原处，当有阴影的这个硬币绕回到原处时，请问它共转了（ ）.

A.360° B.540° C.720° D.900° E.1080°

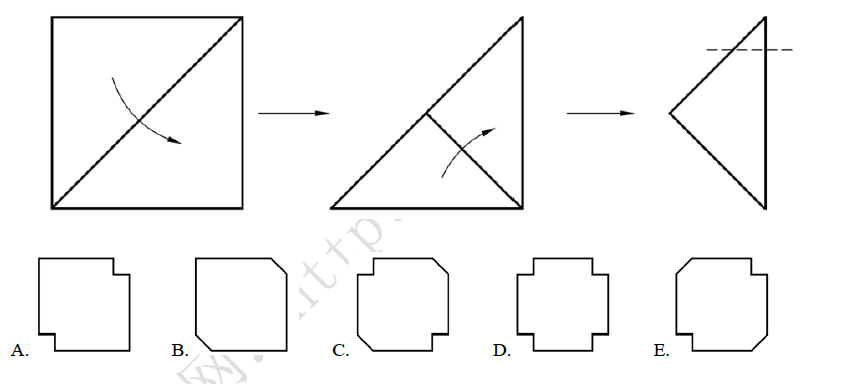
18.依下图所示，将一张正方形纸片沿对角线折叠两次，然后将第三个图沿虚线剪下一小角，再将纸片展开.请问展开后的图形是下列选项中的哪一个? （ ）

19.如图，每两个相邻格点之间的距离为1 cm，则图中阴影部分的面积是（ ）cm2. 这里，数字拐角处是半径为1的圆周的14，𝜋取3.

A.54 B.57.5 C.55.5 D.55 E.以上都不是

20.题图中各相邻边夹角皆为直角，图中共有（ ）个矩形.

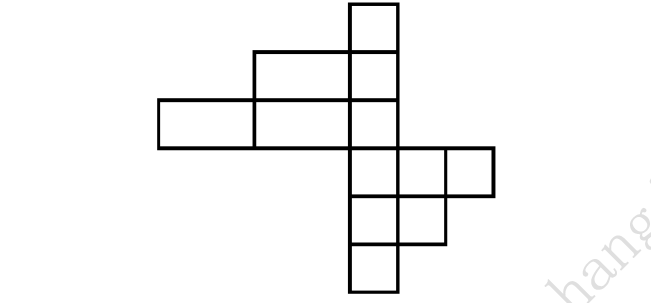
A.39 B.35 C.30 D.25 E.以上都不是

21.在五位数中，共有（ ）个数其任意相邻两个数字之差都为3.

A.50 B.45 C.43 D.40 E.以上都不是

22.在一条公路上，甲、乙两地相距600米，张明每小时行走4千米，李强每小时行走5千米. 8点整，他们两人分别从甲、乙两地同时出发相向而行，1分钟后他们都掉头反向而行，再过3分钟，他们又掉头相向而行，依次按照1，3，5，7…（连续奇数）分钟调头行走.那么，张、李两人相遇时是8点（ ）分.

A.22 B.24 C.26 D.28 E.以上都不对

23.如图所示将五个圆连接起来，现在用三种不同颜色将每个圆涂上一种颜色，且相连接的两个圆不可以涂同一种颜色.那么，可以得到（ ）种不同的颜色模式.

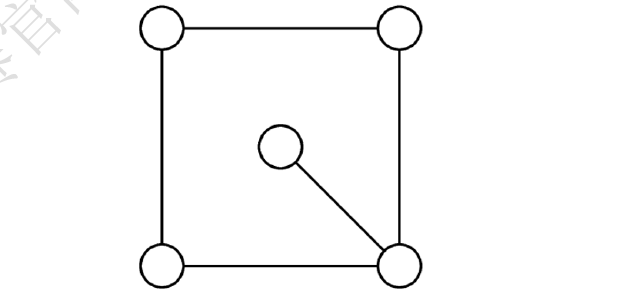
A.36 B.144 C.72 D.32 E.以上都不是

24.如图，在5×5的棋盘上摆放8个○和1个●.

①任何一个棋子都可以沿纵、横、斜向跳过紧挨着的棋子.

②被跳过的棋子从棋盘上拿下.

③要求最后仅把●留在正中间的位置.

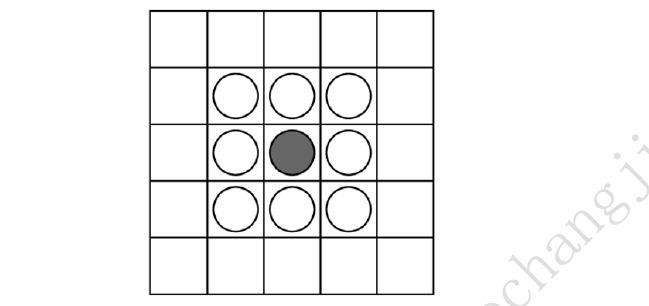
由于每跳一步，棋子就减少一个，所以，不管怎么跳都需要8步.现在，再附加一个条件：

④只要是同一个棋子连续跳过其他棋子，都算一步.那么，最少需要（ ）步.

A.1 B.2 C.3 D.4 E.5

25.五年级（1）班上体育课.如果3人一行剩下1人；如果5人一行，剩下2人；如果7人一行，剩下3人，已知班级人数是个两位数，那么这个两位数的数字和为（ ）.

A.15 B.13 C.11 D.9 E.7

26.如图，正六边形的边长为5cm，分别以正六边形的每个顶点为圆心，边长为半径作圆，各圆交于正六边形的中心.则阴影部分的周长为（ ）cm.（𝜋取近似值3）

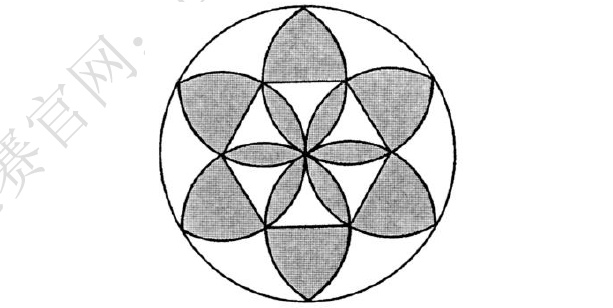
A.100 B.110 C.130 D.140 E.以上都不是

27.将数字0~9各一个填入如图所示的十个六边形中，每个六边形中填一个数字.要求：任意相邻的两个六边形中所填的数字，下层的比上层的大，同层中右边的比左边的大.那么满足要求的不同填法共有（ ）种.

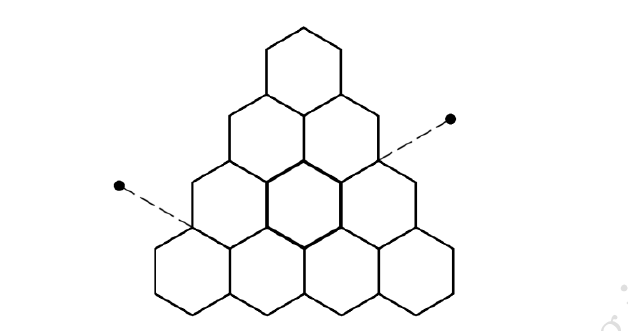
A.3 B.6 C.12 D.18 E.24

28.算式中，相同字母代表相同数字，不同字母代表不同数字，则最后得数为（ ）

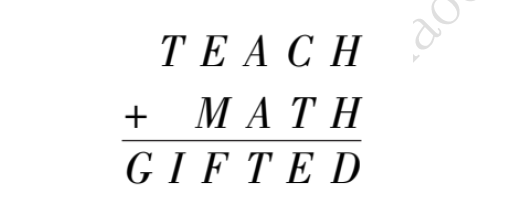
A.102796 B.102022 C.102976 D.202298 E.102967

29.在方格表中选择若干个小方格染成黑色，使得任意一个2×2的方格表中恰有一个黑色小方格.那么这种染法被称为“经典染法”.题图给出了一种6×6方格表中的“经典染法”.显然，2×2的方格表中“经典染法”共有4种.

那么，8×8的方格表中共有（ ）种“经典染法”.

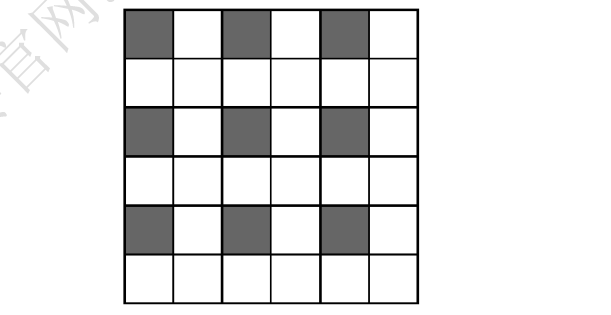
A.12 B.48 C.60 D.75 E.121

30.一共有10个人，其中有些是老实人，他们总是说真话；另一些是骗子，他们总是说假话.他们每个人都想好了一个实数（不一定是整数）.然后，第一个人说“我的数大于1”，第二个人说“我的数大于2”……第十个人说“我的数大于10”.此后，这10个人按某种顺序站成一行，依次说“我的数小于1”“我的数小于2”……“我的数小于10”（每个人刚好说一句）.那么，这些人中最多有

（ ）个老实人.

A.5 B.6 C.7 D.8 E.9