[题目](2022年2月，北京八一学校高三下学期开学考，19)已知函数

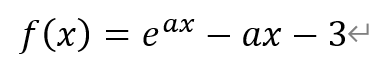
其中a≠0。

（1）求f(x)的极值；

（2）当a＞0时，设函数

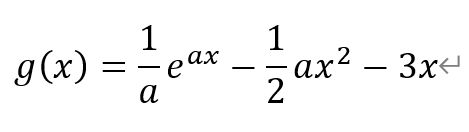
求证：曲线y=g(x)存在两条斜率为-1且不重合的切线。

 

[解析]1）函数f(x)的定义域为R。

对函数f(x)求导，得

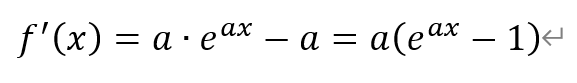
由于a≠0，所以令f′(x)=0，解得

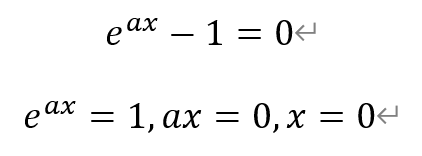
a）若a＞0，则f′(x)的符号与e^ax-1相同。

当x变化时，f(x)和f＇(x)变化情况如下

x	(-∞,0)	0	(0,+∞)
f＇(x)	－	0	＋
f(x)	↘	极小	↗

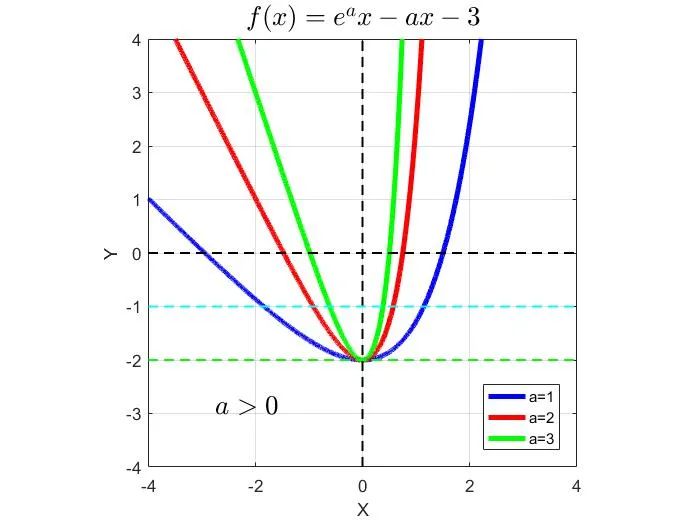
b）若a＜0，则f′(x)的符号与e^ax-1相反。

当x变化时，f(x)和f＇(x)变化情况如下

x	(-∞,0)	0	(0,+∞)
f＇(x)	－	0	＋
f(x)	↘	极小	↗

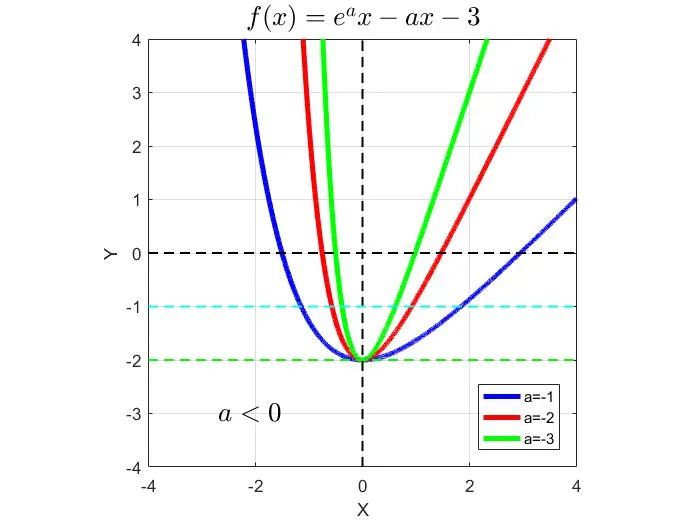
综上，函数f(x)在x=0处取得极小值，即

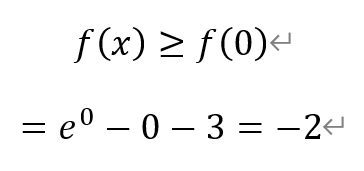
因此，函数f(x)在x=0处取得极小值-2，无极大值。

 

2）函数g(x)的定义域为R。

当a＞0时，对函数g(x)求导，得

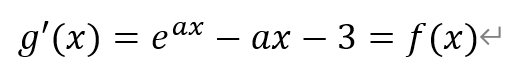
由1）可知，函数f(x)在x=0处取得极小值-2。注意到，

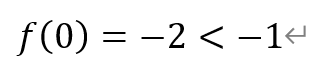
以及

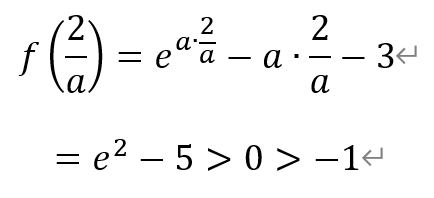
和

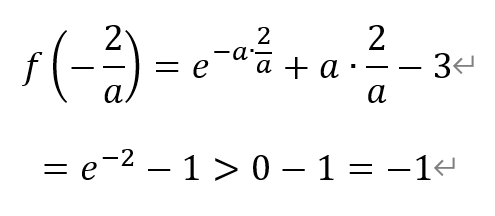
根据零点存在定理，函数f(x)在(-a/2,0)和(0,a/2)上各存在一个零点。

设x1∈(-a/2,0)和x2∈(0,a/2)。下面只要证明，函数f(x)在P1(x1,y1)和P2(x2,y2)处的切线不重合即可。

函数f(x)在Pi(xi,yi)，其中i=1,2，的切线方程为，

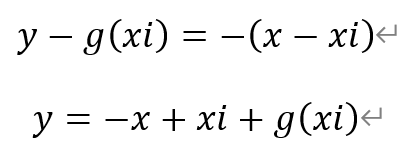
假设这两条切线重合，则有

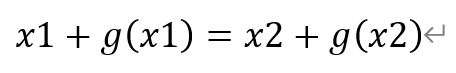
构造函数t(x)，

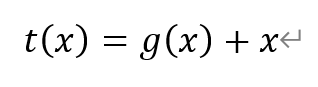
则有

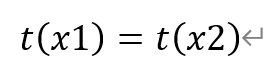
对函数t(x)求导，有

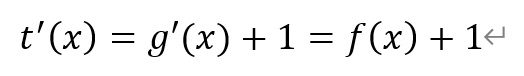
由1）可知，当x∈(x1,x2)时，f(x)＜-1，即t′(x)＜0，函数t(x)单调递减。于是有

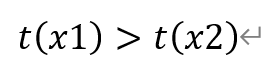
推出矛盾。因此，假设不成立，即函数f(x)在P1(x1,y1)和P2(x2,y2)处的切线不重合。命题得证。