很多时候，数学的思想隐藏在形式和术语浓雾背后。我们应该学习如何穿越这片迷雾，以便清楚地获得想法（Ideas）、概念（Concepts）和隐藏极深的背后观念（notions），写下来，画出来会非常有价值。

-纽约大学数学家戴达娜·布拉德利

---

今天偶然间看到这份《2022年丘成桐少年班招生试题》，不知真假，但内心无疑希望这是丘老对数学的期望和理念。数学教育的创新和变革迫切需要丘老这样的榜样及数学大师的引领。数学教育创新的关键是：更好地评估和选拔方式。如果没有数学评估方式的创新，也很难有数学教育快速进步与发展。

备注：本试卷共6道题目，开卷答题，时间自定，建议时间：一周以内完成。

---

第一题：数学史

请自行查阅资料，了解人类主流数学史的发展脉络，并以5-8个著名数学家为例，按出生的先后顺序举例说明他们所作出的贡献对世界数学发展的影响。（字数不限，手写作答。以逻辑清晰，语言表达清楚，作答书面使用手段等为主要评分标准。）

考察重点：从数学家身上寻找数学家思考方式+榜样的力量+方法论。

---

第二题：数论

请讲讲你认为的“数论”是什么？并以1-3个问题为例做说明，并编制一道你认为非常难的数论题。（字数不限，手写作答。以逻辑清晰，语言表达清楚，作答书面使用手段等为主要评分标准。）

考察重点：知识的深度和数学家思维。

人类想要完全了解质数，至少还需要100万年。   

—20世纪的欧拉，匈牙利数学家保罗·埃尔德什

---

第三题：平面几何

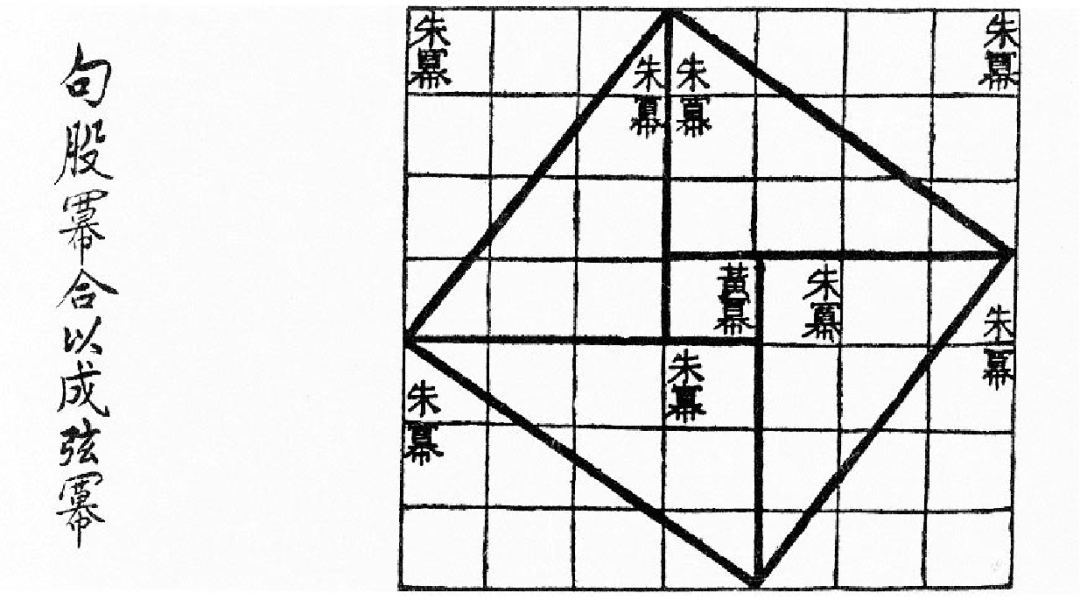
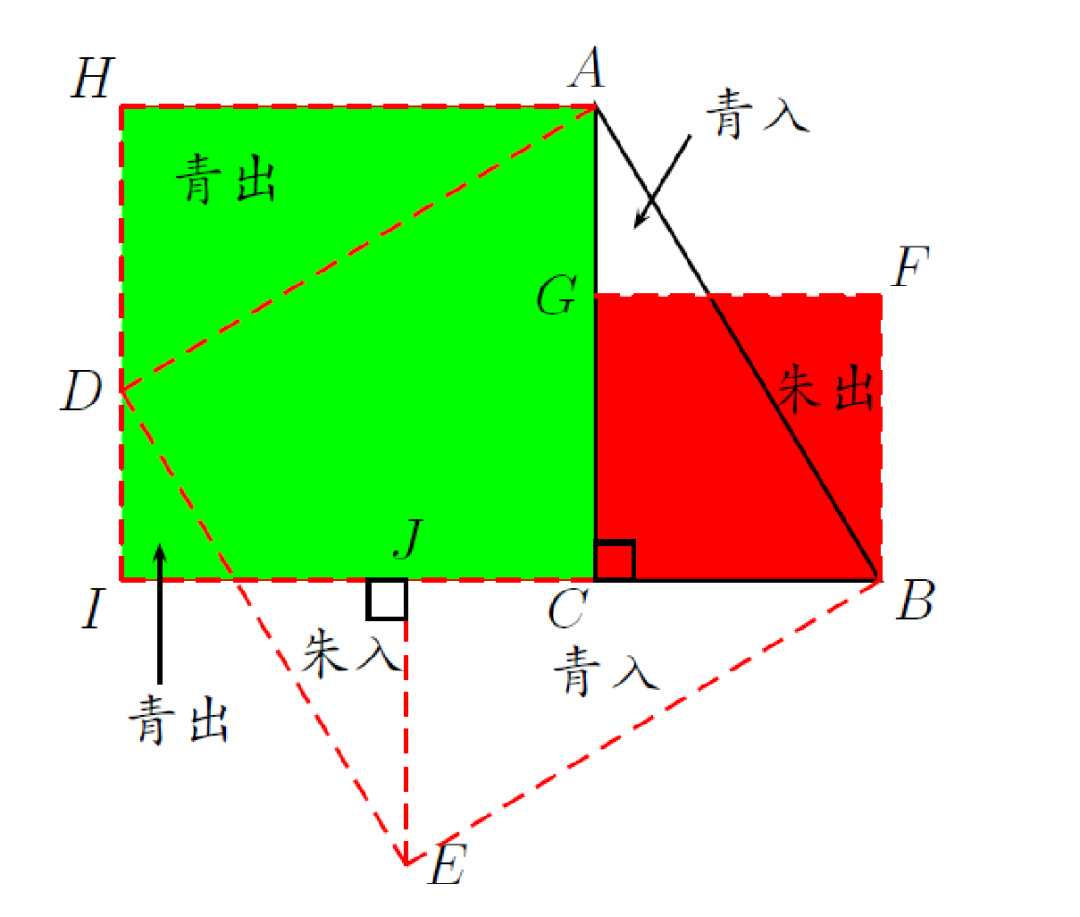
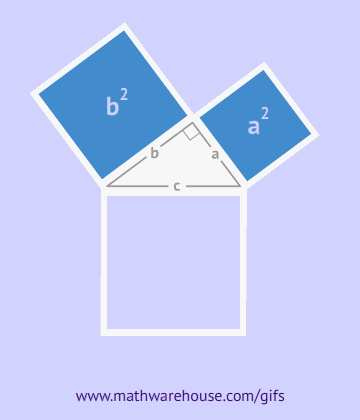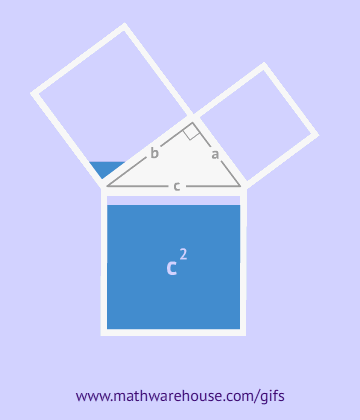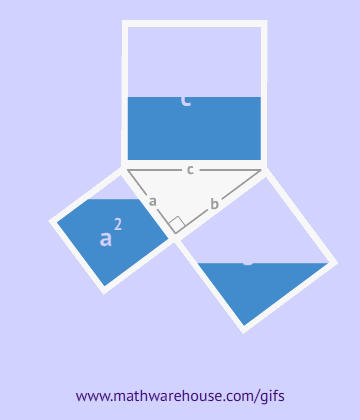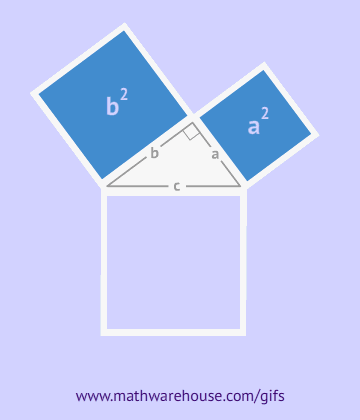
请花一定的时间阅读《几何原本》第一卷内容，用先“理由”再“结论”的格式写出命题47的完整证明过程。（依然使用欧几里得的证明方法，只是格式不同，其中“理由”部分直接写出内容，而不是用“公设n”或者“命题m”替代）

考察重点：证明的逻辑和创新艺术。

数学证明Proof是指人们为获得使人信服的数学结论所采用的手段。在现实生活中，我们经常使用“实践证明”、“历史证明”、“实验证明”、“举例证明”等多种形式来说服他人．而在数学中，对数学结论的正确性进行证明，更为严谨，更为严格，被证明过的数学公理被人们视为法律的基础，无容置疑。 

数学证明Proof就是利用已知条件、定义、公设（基本事实）、公理、定理进行推理的过程，在证明过程中每一步推理都必须有上述依据，不能想当然。

学习证明就是培养严谨、理性的思考方式。

有些数学证明如此美妙，只能是上帝的创造，数学家不过是幸运地发现了他们而已。

—20世纪的欧拉，匈牙利数学家保罗·埃尔德什

第四题：统计与概率

在丘成桐先生自传《我的几何人生》中有三篇序，正文十二章，附录文章五篇，后记一篇，请你估算“我”字出现在本书中的总次数。（写出自己的估算方法，字数不限，手写作答。以逻辑清晰，语言表达清楚，作答书面使用手段等为主要评分标准。）

考察重点：统计学应用，词频统计学

红楼梦词频统计：横坐标是章回编号，纵坐标是“笑道”的词频

第五题：文献检索

未来之路，需要学习很多东西，而且很多东西需要我们自己去寻找，所以我们要学会文献检索，请你想办法在“百度”、“知网”等网站查阅并整理下面关键词的内容：“小升初”，“小学数学和初中数学的差别”，“中考数学”，“初中数学和高中数学的差别”，“高考数学”，“数学竞赛”，“中学数学和大学数学的差别”等内容，自行选择一条脉络，下载相关文献（10篇左右），按自己的逻辑顺序整理，并写一点心得。（字数不限，手写作答。以逻辑清晰，语言表达清楚，作答书面使用手段等为主要评分标准。）

考察重点：研究技能+数学思想

小学：算术思维+几何

初中：代数思维+部分函数+代数与几何笛卡尔坐标系下的跨界打通

高中：函数语言+微积分

---

第六题：意志与品德

子曰：“譬如为山，未成一篑，止，吾止也；譬如平地，虽覆一篑，进，吾往也。”

考察重点：热爱与坚持

数学无它，须建立系统知识框架体系，追求卓越与完美，只需坚持即可。