浅析丘成桐少年班几何题一例（增补）
-
-
上海小升初 这家伙很懒，还没有设置简介
0 人点赞了该文章 · 119 浏览
构造等角证明此题
这个证明主要思路是把目标想证明的角尽可能集中起来。
观察图形可以发现，需要证明相等的两个角中，角AFB可以通过圆周角的性质和平行四边心ABCD的一些角关联起来，而角DFE暂无法与这些角关联。
不过，很明显角DFA倒是可以直接与这些角关联起来，都对着同一个劣弧AD的角DFA = 角ABD。于是，简单粗暴，我们直接在角ABD处“无中生有”构造出一个角出来，比如角MBN = 角EFC，这样一来，问题就转化为求证角NBC = 角DCA。
这么看就舒服多了，因为，我们一眼看见(B,N,E,F)四点共圆，这样一来，有很多等角和结论等着我们。
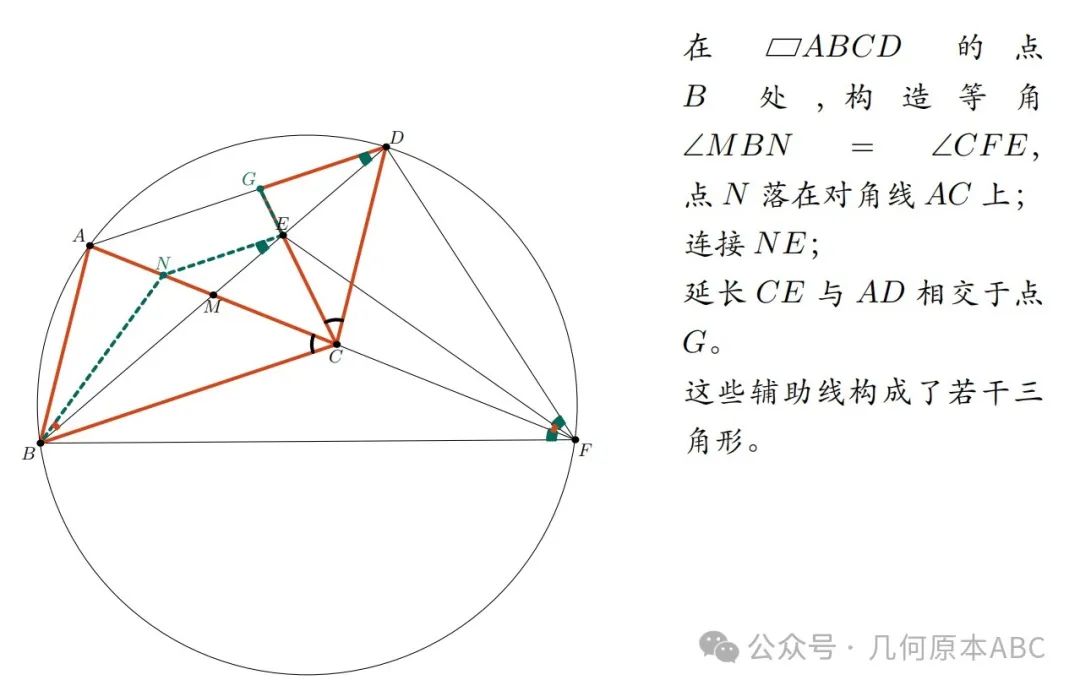
简证如下：
全部 0条评论