陪位中线

定义：三角形的陪位中线（Symmedian）指的是三角形一条中线对于其对应的顶点的等角线。也就是说，由三角形的一个顶点向对边所引的中线，并且，中线与邻边所构成角与陪位中线与另一个邻边所构成角是相等的，这条等角线被称为陪位中线。

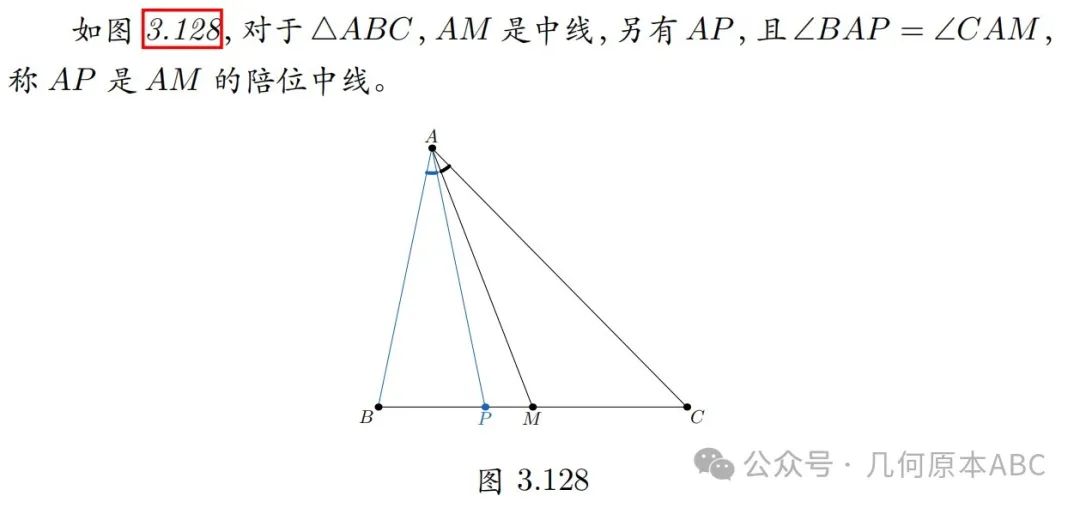
    陪位中线有一些有趣的性质，中学数学竞赛中常见的性质包括：

性质1:

性质2:

AP延长线与经过B,C两点的三角形ABC的外接圆的切线交点D三点共线。

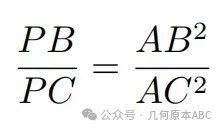
    其中，性质1是陪位中线在证明中常用的结论，性质2是陪位中线的作图法。

    我们先用性质2作图得到陪位中线，并证明，在这种作图下，角CAM = 角BAF。然后，我们再证明性质1。

    利用性质2的作图如图3.129：

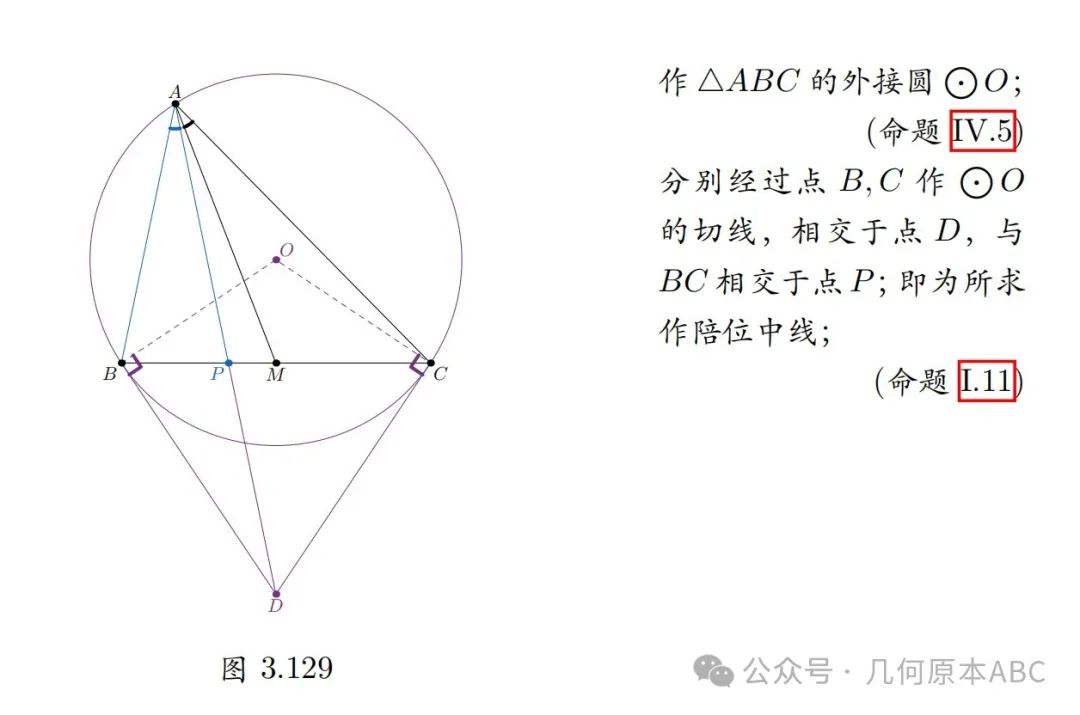
    对作图的证明如下：

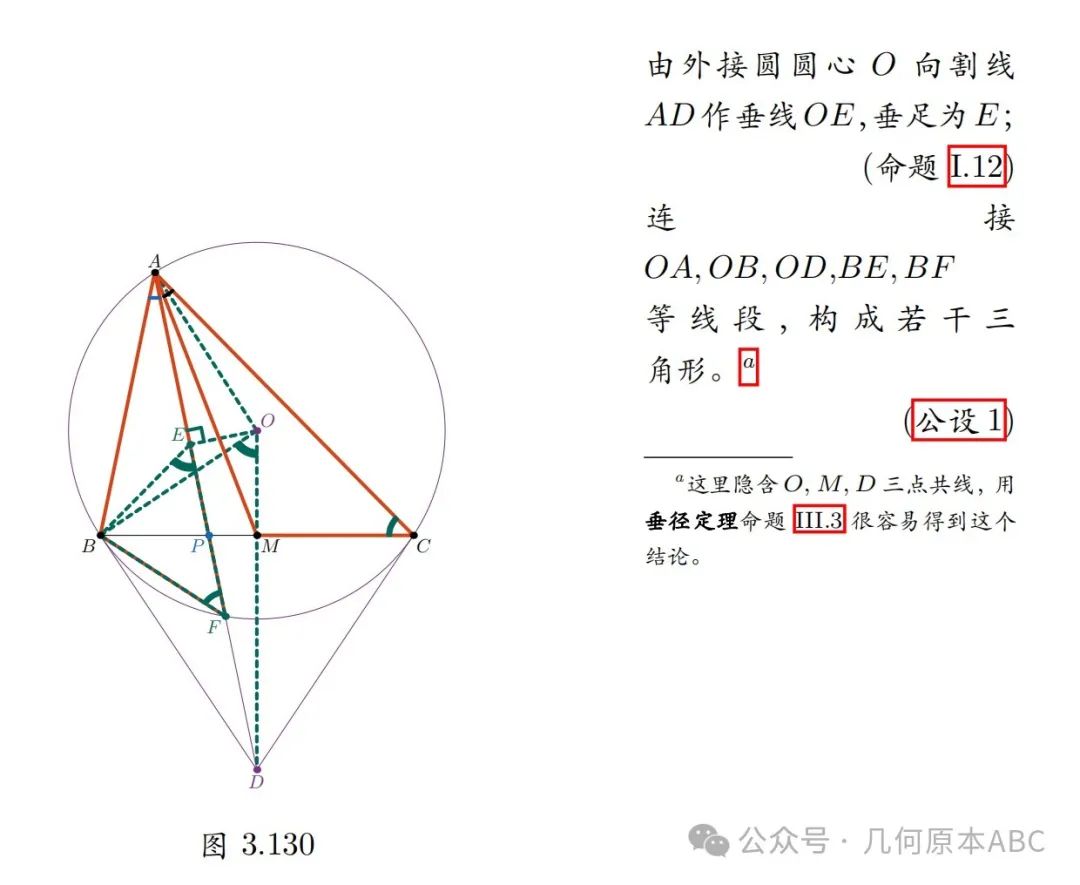
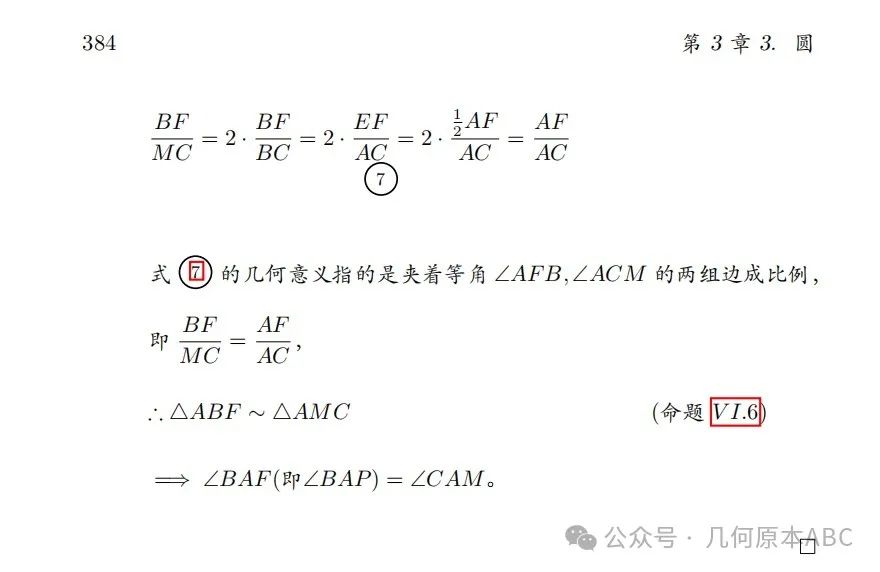
    这个作图法的证明启发了我们，还有一种作图法同样可以得到陪位中线，如下图3.131：

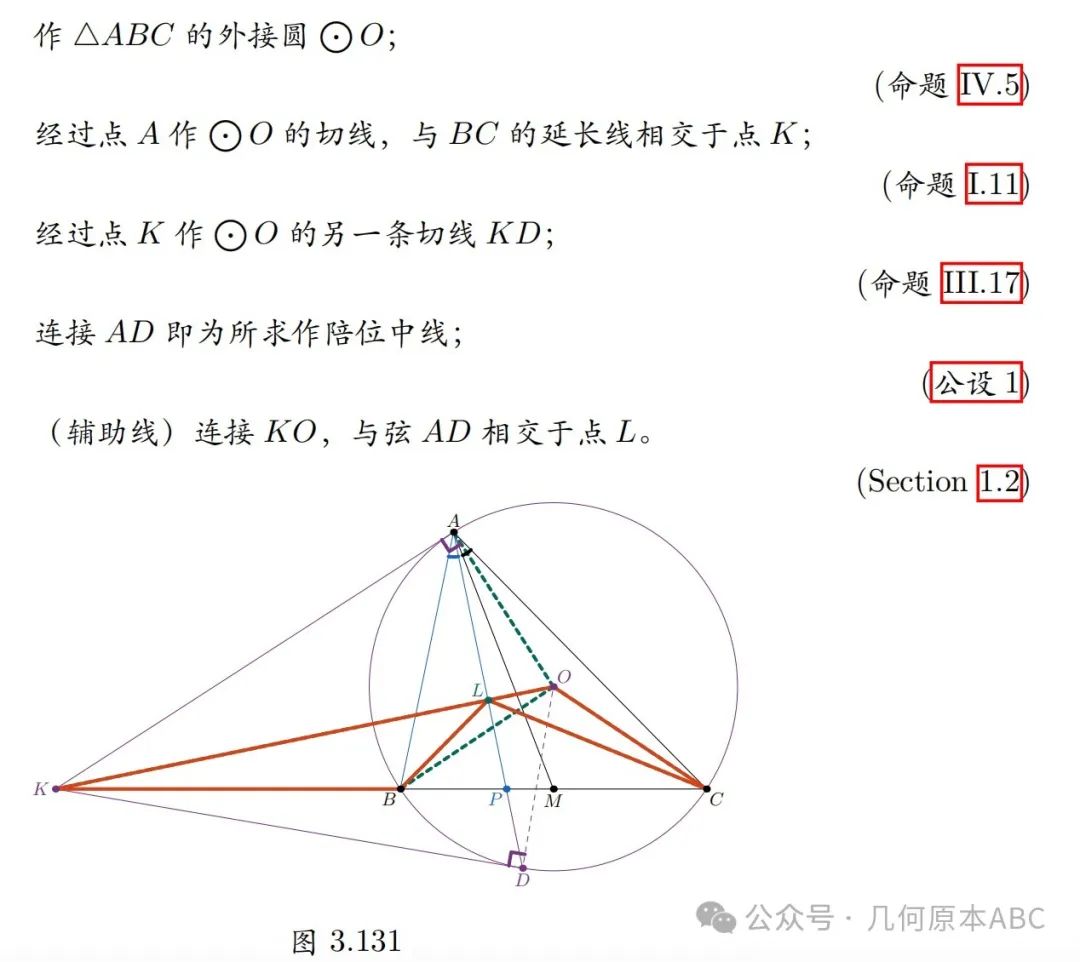
    这个作图法下的证明如下：

    接下来，我们证明陪位中线的性质1，证明辅助线如图3.132：

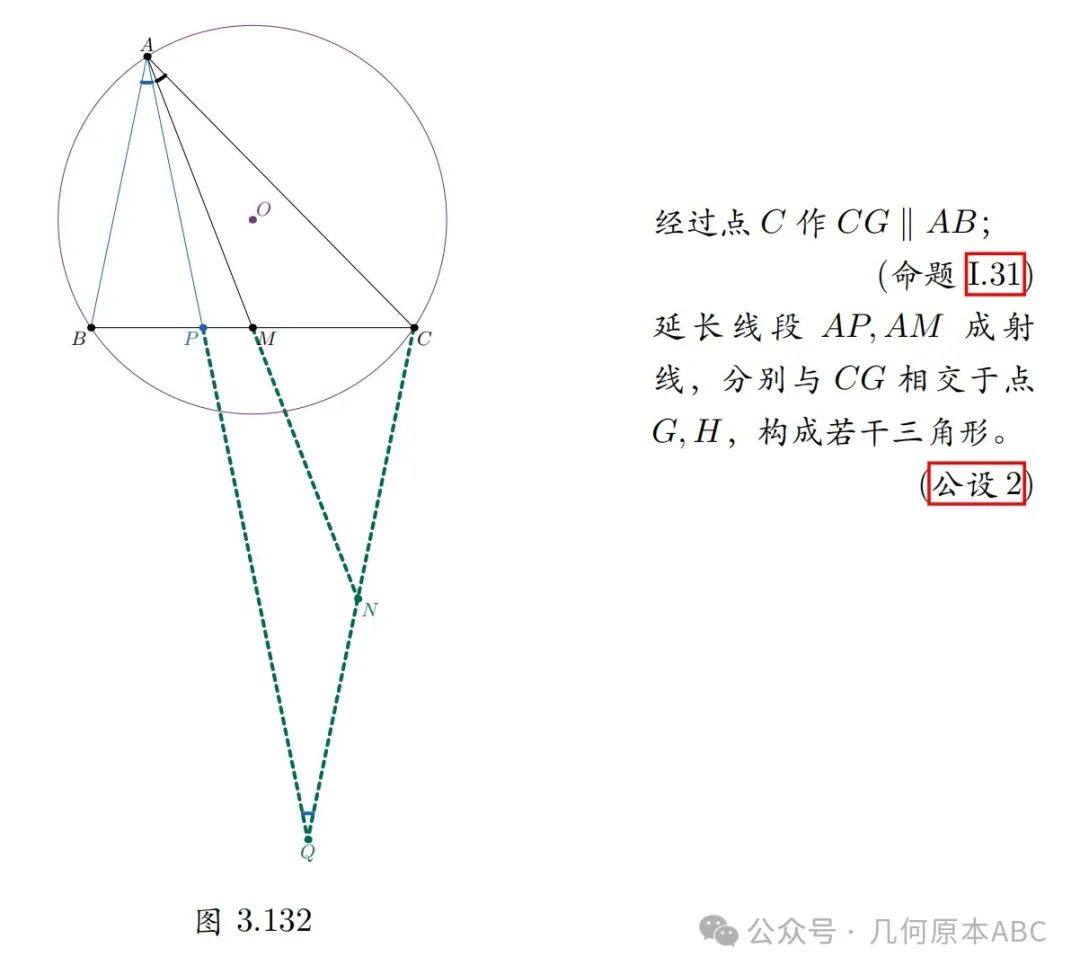
    证明如下：

利用陪位中线的性质证明此题

    好了，我们已经了解并掌握了陪位中线，翻过头来再看此题，应该有洞若观火的感觉了。

    很显然这道题的图形构造了两组陪位中线。我们设平行四边形ABCD的对角线交点是M，第一组陪位中线是三角形BCD顶点C处的CM,CE，第二组是三角形BFD顶点F处的FM,FE。

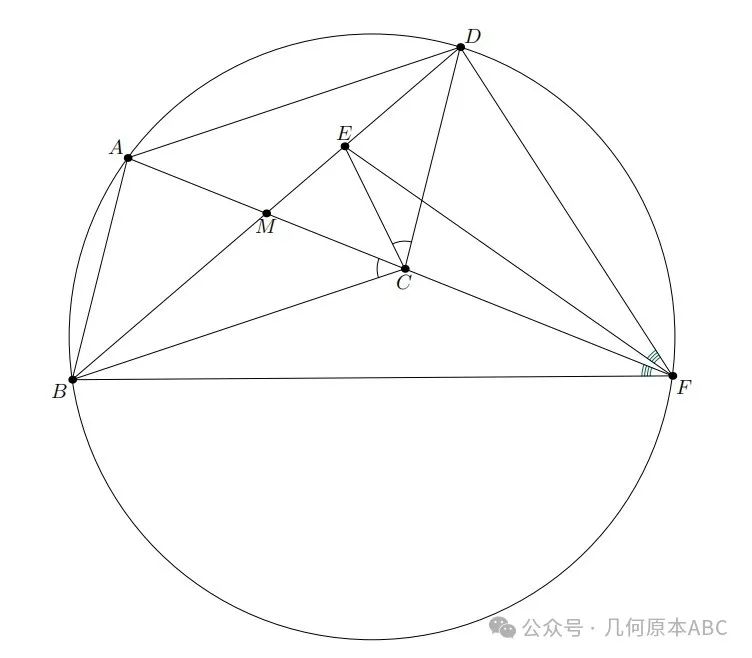
    对三角形BCD用陪位中线的性质，得到：

    那么，问题由证明角DFE = 角AFB转化为证明：

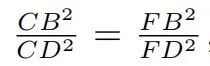
    进一步利用平行四边形对边相等的性质，需要证明：

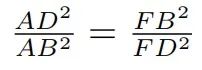
    即，

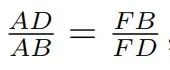
    将这个比例式换成等积式可能更清楚些，即求证：

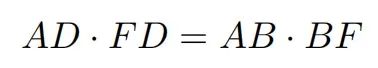
    简证如下：

总结    

    至此，这道题的来龙去脉得到了比较详尽的解释。陪位中线的相关性质很有趣。并且，相比于性质，其证明思路也是很巧妙的，我很喜欢证明中图3.130，从三角形BEF相似于三角形ABC，通过边的性质过渡到三角形AMC相似于三角形ABF的证明过程，用到了《几何原本》第六卷“相似形”第6命题。让我对这个命题的真实意思有了深入的理解。

    最后，小结一下证明中主要用到的《几何原本》中的命题：

• 圆幂四定理之：托勒密定理。

• 相似三角形判定：【命题VI.2】、【命题VI.4】、【命题VI.6】、射影定理【命题VI.8】

• 圆的相关结论：垂径定理【命题III.3】、【命题III.20】、四点共圆判定【命题III.22】、切割线定理【命题III.36】

• 三角形性质：陪位中线【定理II.2】（《几何原本ABC》）