看懂，北京2023年中考数学，意味就有2024考向。

1.试卷源于网络，文末下载近十年北京中考数学真题2.文中会阐述每道题的前世今生，看完需要点耐心

2023年北京中考数学考点详情

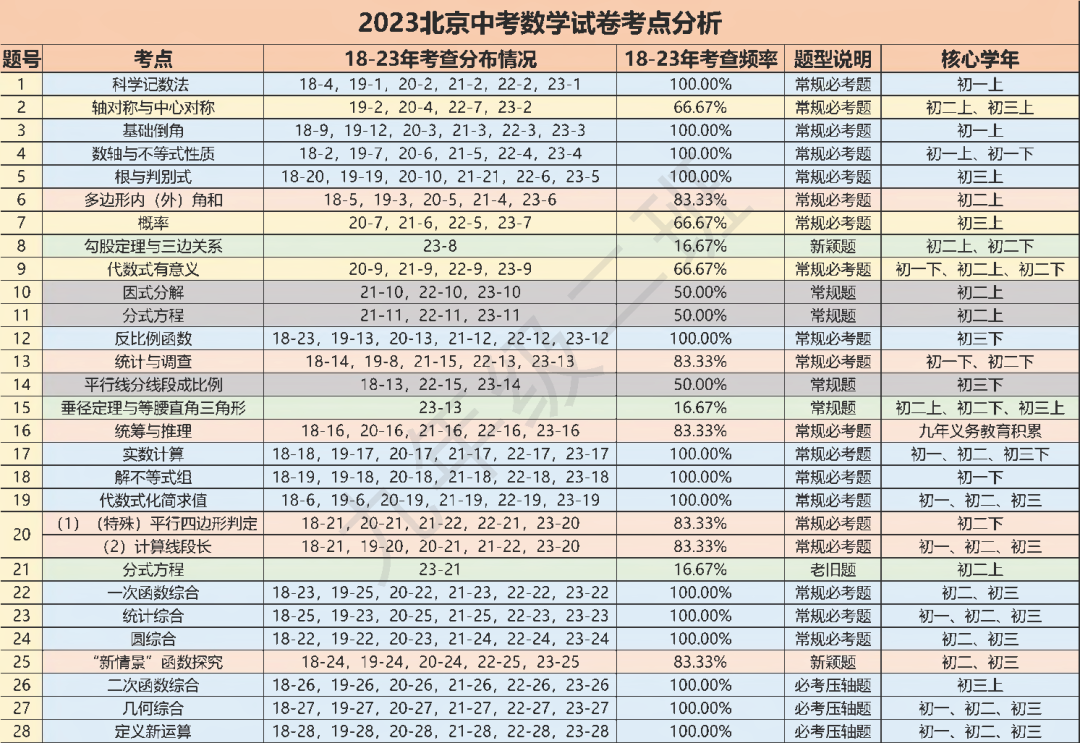
第1-7题，对基本知识的考查，整体上比较常规，题目顺序的设置较稳定，只需要认真审题，细心计算即可。

第8题，今年的新颖题。考前我课上跟小朋友们预测今年大概率还会和22年中考保持一致，主要是基于前些年的考法实在是没啥新花样了，23年一模除了通州区，其他城区延续了22年中考的形式，考查函数的定义或性质，没想到中考完全的大变样。虽然这道题难度并不是很大，但是突然的风格切换，反而成了孩子们心理素质的考察，这就要求孩子们平常心，处变不惊。

第9-15题，对基本知识的考查，比较常规，平常只要刷了中考真题，一模二模试卷，基本上都是轻车熟路。不过我在这里事后诸葛亮一下，这几道题还是要有速度才可以，磨蹭不得。

第16题，从20年开始考查到现在，没啥具体的知识点，方法是也比较发散，就是考查小朋友们的逻辑推理能力，更多是生活常识、思考经验等的积累。往往都是设置两个空，第一空较为简单，第二空综合较强，可以战略性思考。

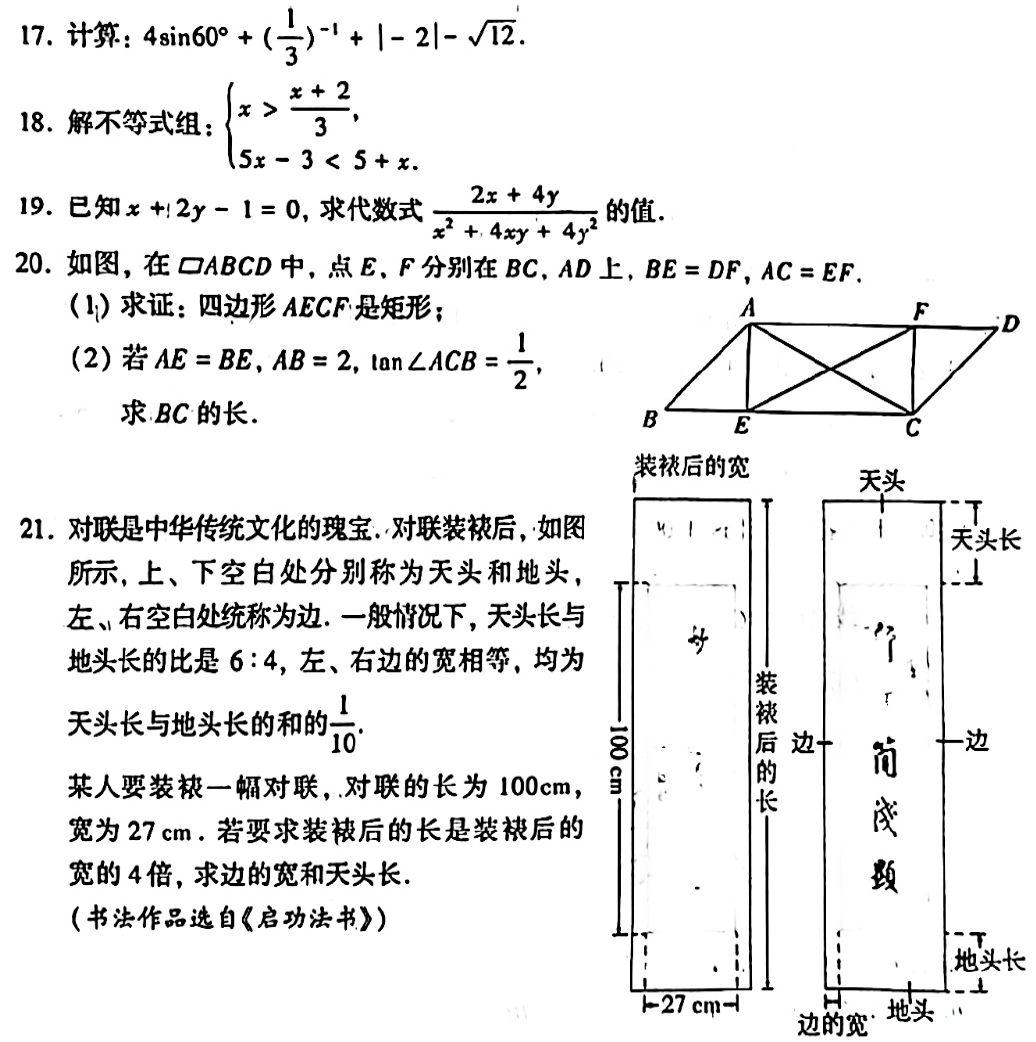
第17-20题，常规必考题，同样平常只要刷了中考真题，一模二模试卷，基本上都是轻车熟路，所以，该刷还得刷。

第21题，题目给的背景很有创意，不得不说真的接地气。但是对小朋友们的审题要求挺高的，看懂这个背景和示意图，明确所求问题，合理设置未知数，环环相扣，一点都马虎不得。不过题目本身的考查点属于老旧题了，毕竟是15年中考的形式，是不是也在暗示我们，中考过上个三五八年的，也要适当的往回看看呢？

第22题，一次函数综合，常规必考题，基本功扎实就很轻松，一次函数这几年本来也越来越轻松了。

第23题，第三问的条件非常有创意，我想说这样的描述基本上解题方法一定不是硬算，必定是靠审题和理解，这里就是高手过招，妙趣横生了。

第24题，圆综合。这题真的是考小朋友们心理素质的，简单也是，难更是。如果能轻松拿下，似乎预示着后面可以一马平川，要是感觉费劲，似乎后面有点挑战。毕竟，圆综合往这里一放，就意味着接下来要爬坡了。平常很多小朋友都不能一口气拿下来，形成了战略上解题。但是，说实话，圆综合是有套路的，至少我是给小朋友们反复强调过的，真没那么恐怖。总之，如果说前面说的常规必考题刷题能解决，那么，圆仅仅是刷题还不够的，一定要总结，找到定式思维。

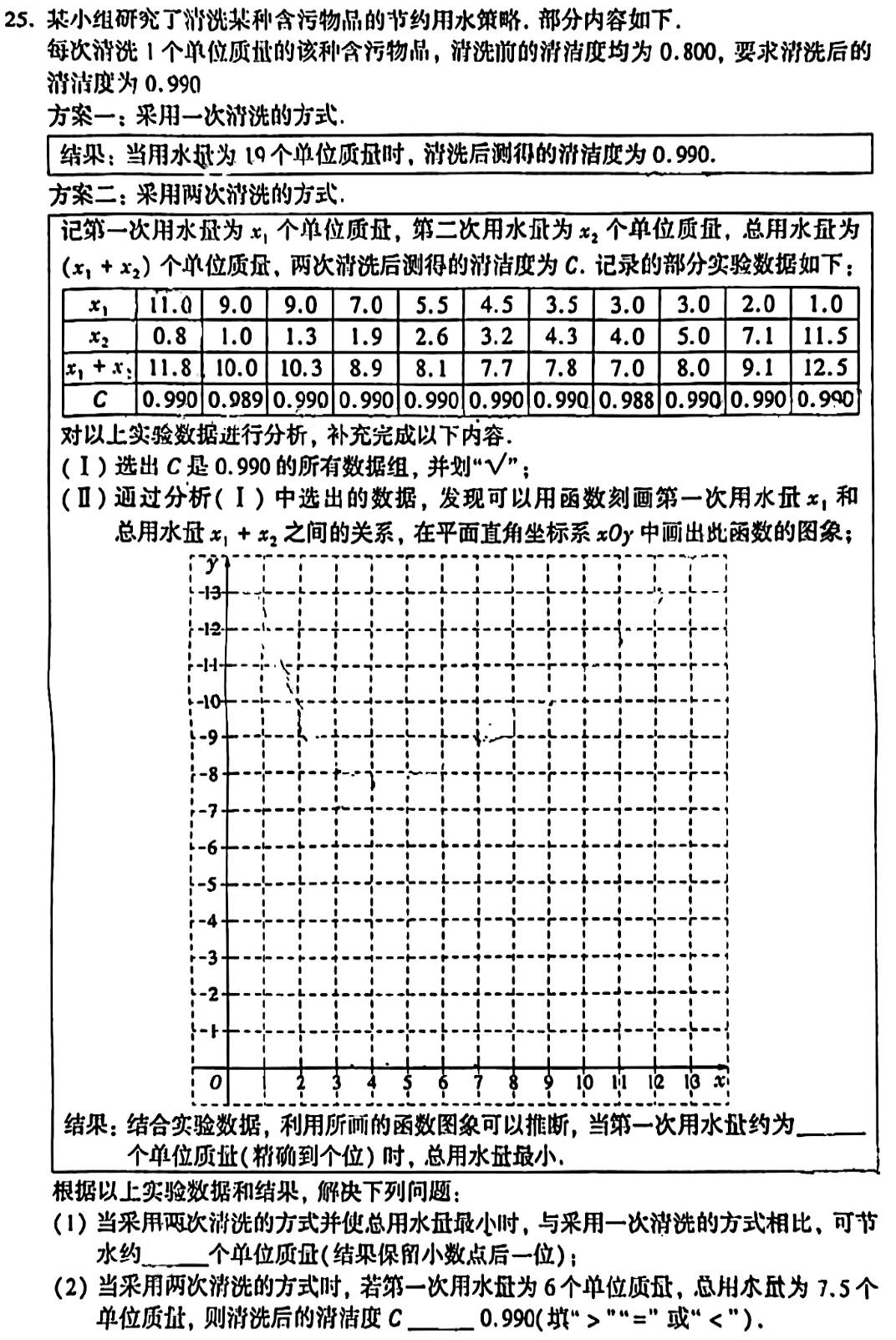
第25题，这题我都没想好该怎么称呼它。从迭代思维来看，早在14年中考的第8题出现函数与图象考查（跟23年部分城区的一模第8题类似）后，15年中考的第26题，16年中考的第26题为函数探究的第1.0版本，它们注重的是函数本身图象与性质的考查；接着以17，18，19年的中考为代表的函数探究的第2.0版本出现了，它们注重的是函数的探究，发散性、综合性都更高，随之而来的争议性也更大了。所以，在20年的中考中又回到了基于1.0版本的1.5版本，探究函数本身的性质，同时要运用性质去解决问题。21年，有点意思，直接取消不考了。22年改头换面，王者归来，以二次函数为载体的函数探究与应用，形式变了，运用多了，显然这是3.0版本。到了今年，可谓再上一层楼，姑且叫它4.0版本，阅读量明显增加，情景格外新颖，信息理解力要求明显变高，运用与分析能力也有了一定的要求，可以说，它融合了1.5版本的描点作图，2.0版本的性质分析，3.0版本的理解运用。但是，但是，但是，却基本不用计算。也就是说，小朋友们，语文的阅读理解+数学的逻辑推理，是多么的无敌。

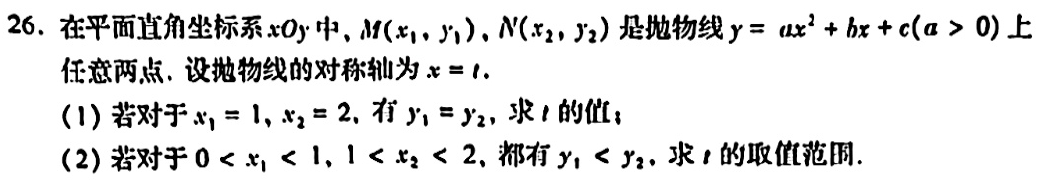
第26题，二次函数综合。从15年的常规交点问题，到19年的双动问题，再到20年及以后的增减性与对称性问题，也是经历了好几拨迭代的。不过，小朋友们看到这题后，比起上面25题的变化，这道题应该是找到了熟悉的感觉，算是稳定军心了。这类题方法得当基本就是秒，方法不当，无论怎么画图，要从不确定中找确定性，还是很糟心，所以，在我看来，这道题从来都不是考学生，是考老师的水平。

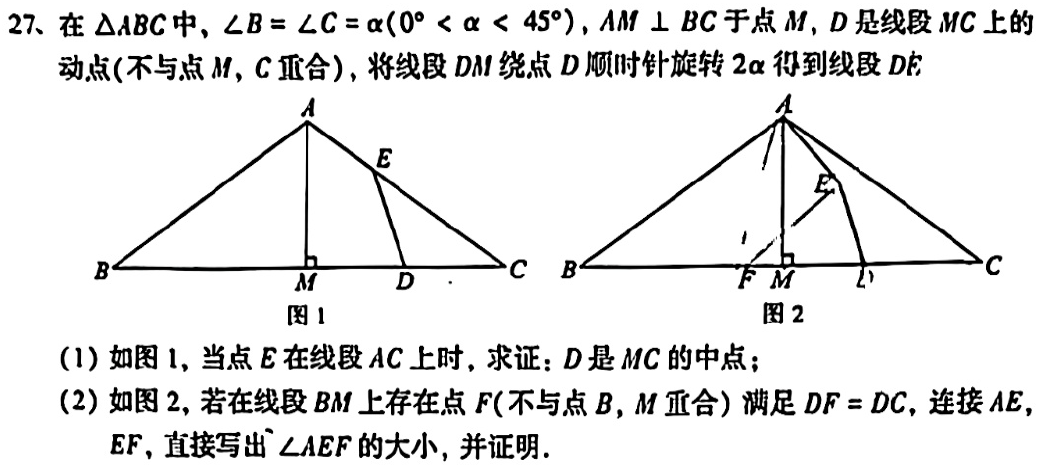
第27题，几何综合。考场上再次见到中点，肯定是既熟悉又陌生，毕竟连续四年都是这个。第一问是真的“送”，第二问也是真的“送”，只是谁送谁的区别。中点常考的就是倍长中线，三线合一，中位线，斜边中线，平行线分线段成比例（本质是中位线），勤思多练，多总结方为上策。几何综合模型还是很重要，虽然越来越灵活，但是模型就是启发点和确认点，会与不会，区分还是很明显的。

第28题，新定义。每一道新定义都很有意思，但是要想每道新定义都能搞定，还是需要一点上帝视角的，这里我就不多说了。

根据近几年北京中考数学试卷，题型分值如下:选择题8道各2分共16分，填空题8道各2分共16分，解答题12道共68分(前9道各5分，后3道7+8+8分)，合计总分100分，时长120分钟。

从历年中考数学评卷情况来看，考生出现失分情况，有以下特点：如审题不仔细、基础知识掌握不牢固、运用知识能力关、答题不规范等等。结合题型及失分原因分析如下：选择题失分原因主要有以下两方面：

（1）基本知识不牢固，

（2）推理能力差

填空题涉及的知识面较广，除注重对学生基础知识与基本技能的考查外，还关注学生问题解决能力的考查，学生错误主要集中在压轴题，需要分类讨论，容易产生漏解，如果平时缺乏类似的训练，学生较易出现错误。

解答题主要考查学生的基本运算能力，数学语言的表达能力，获取并整合信息的能力、解决实际问题的能力等等。在阅卷过程中解答题失分原因主要分为以下几点：

（1）缺乏良好的书写习惯 如证明全等时对应字母位置写错，造成失分；

（2）解题不够细心认真；

（3）书写不规范，卷面书写混乱造成失分；

（4）缺乏应用意识及对现实问题的认识；

（5）缺乏解决综合性问题的能力和信心。

数与代数式常考考点：1.选择题第1题基本上考查实数的相关概念，多为相反数、绝对值或有理数的大小比较的考查；对科学记数法的考查近几年每年必考一次；对统计数据的分析或统计量的判断在每年的选择题中都会考查；填空题第1题多为实数的运算对概率的考查每年都在填空的12题或13题中考查，一般为简单概率或放回与不放回模型概率计算；对不等式组的考查与一次函数图像与不等式结合的考查在近三年中选择题也比较常见；对函数的考查中必有一个为二次函数的考查，填空题中为反比例函数与几何或二次函数与几何的综合类型

几何部分部分常考知识点：对视图的考查一般多在选择题中每年出现一道试题；每年必会进行平行线或作图相关的角度计算问题考查；对圆部分一般考查在选择题与填空中各考查一道，选择题中考查对切线、垂径定理与圆周角定理的运用、填空题中考查弧长或圆锥展开图及扇形面积相关的计算；对阴影面积的计算 是每年填空题必考内容；填空题的压轴题多以几何图形的折叠或旋转相关，涉及多种数学思想方法的运用。