2021-2022学年北京朝阳高三上学期期末数学试卷解析几何解答题解析
-
-
梁老师 北京小升初老师～
0 人点赞了该文章 · 99 浏览
[题目](2022，北京朝阳高三期末，19)已知曲线W：
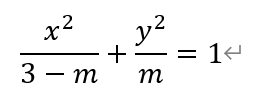
(m∈R，m≠0，且m≠3)。
（1）若曲线W是焦点在x轴上的椭圆，求m的取值范围；
（2）当m=1时，过点E(1,0)作斜率为k(k≠0)的直线l交曲线W于点A,B(A,B异于顶点)，交直线x=2于P。过点P作y轴的垂线,垂足为Q，直线AQ交x轴于C，直线BQ交x轴于D，求线段CD中点M的坐标。
[解析]1）由于椭圆W的焦点在x轴上，所以有
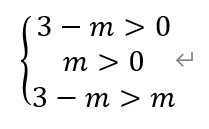
解得
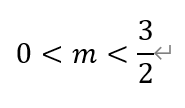
因此，m的取值范围为(0,3/2)。
2）当m=1时，椭圆的方程为，
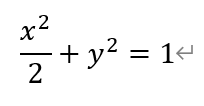
由于k≠0，所以设直线l的方程为：x=ty+1。
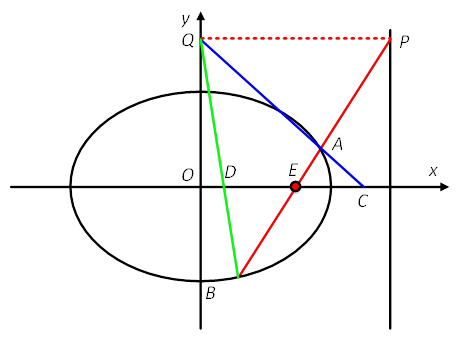
与椭圆W的方程联立得，
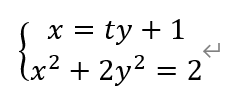
消去x，得到一个关于y的一元二次方程，
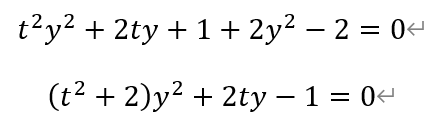
其中，
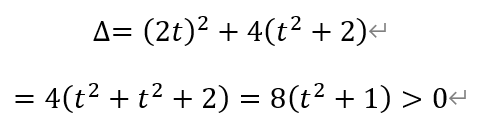
设A(x1,y1)，B(x2,y2)。利用根与系数的关系，得
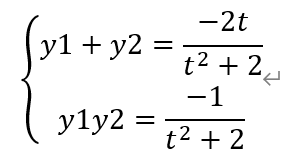
注意到
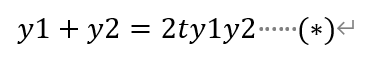
对于直线l，令x=2，有
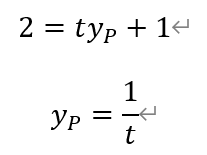
即有
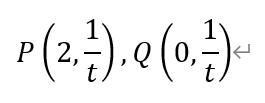
直线AQ的斜率和方程为，
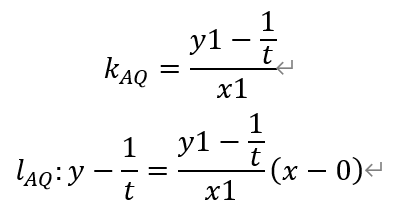
令y=0，解得，
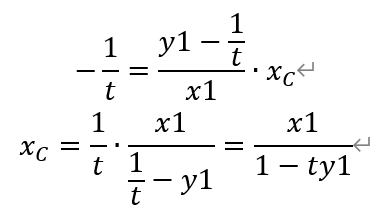
即有
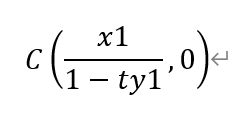
同理，有
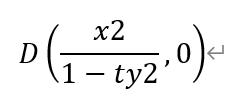
于是，点C和点D的中点M的横坐标为，
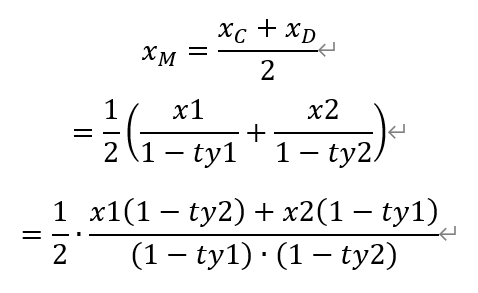
其中
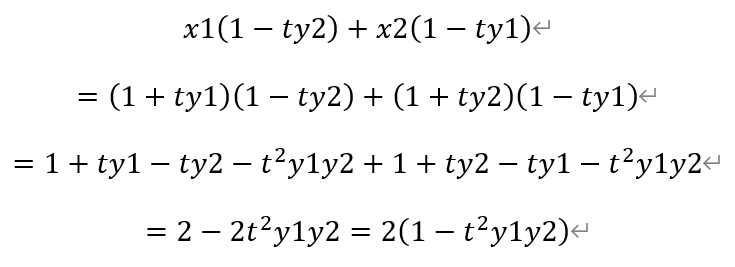
以及，
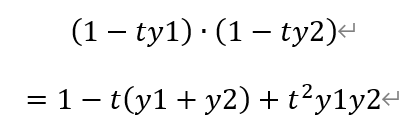
将(*)代入，得
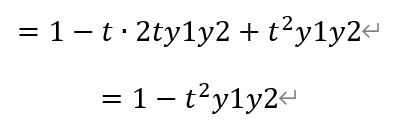
从而有，
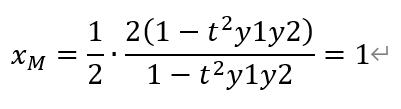
即线段CD的中点M的坐标为(1,0)。
全部 0条评论