[题目](2022，北京海淀高三期末，19)已知点A(0,-1)在椭圆C：

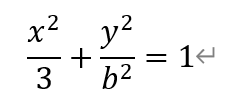
（Ⅰ）求椭圆C的方程和离心率；

（Ⅱ）设直线l：y=k(x-1)(其中k≠1)与椭圆C交于不同两点E,F，直线AE,AF分别交直线x=3于点M,N。当△AMN的面积为3√3时，求k的值。

 

[解析]1）由于椭圆C过点A(0,-1)，所以b=1。于是椭圆C的方程为，

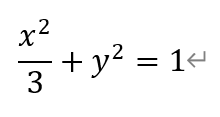
根据椭圆的性质有，a=√3，c²=a²-b²=3-1=2，c=√2。于是，离心率e为，

 

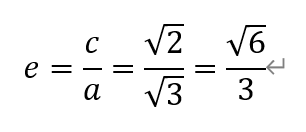
2）由于直线l过定点(1,0)，所以考虑将直线方程换为横截式。

首先考虑k=0的情况：当k=0时，直线l的方程为y=0。则点E(-√3,0)，点F(√3,0)。直线AE的斜率和方程为，

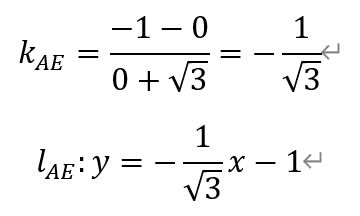
当x=3时，解得

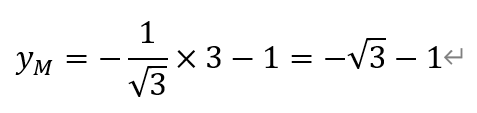
因此，点M的坐标为，

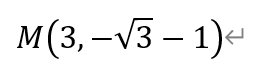
同理，可得点N的坐标为，

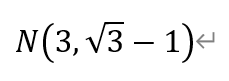
于是，△AMN的面积为，

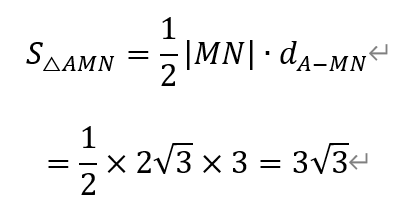
从而，k=0是其中一个解。

 

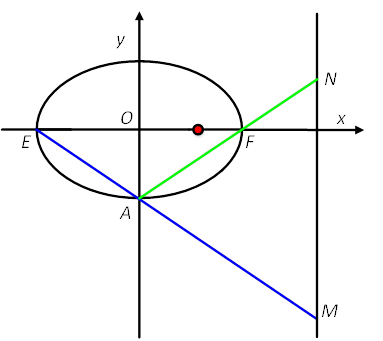
然后考虑k≠0的情况：当k≠0，设直线l的方程为：x=ty+1。与椭圆C的方程联立得，

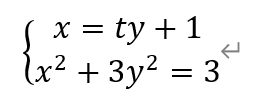
消去x，得到一个关于y的一元二次方程，

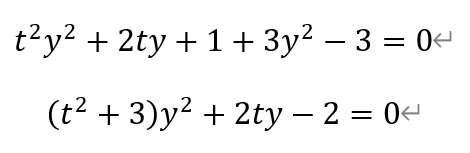
设E(x1,y1)，F(x2,y2)。其中，

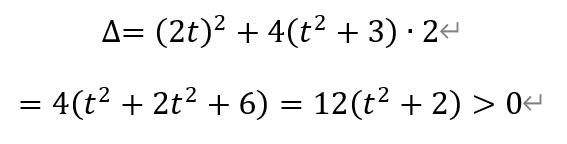
利用根与系数的关系，得

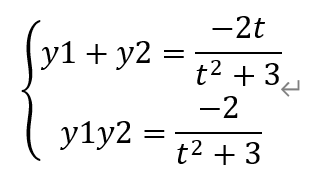
由于A(0,-1)，所以直线AE的斜率和方程为，

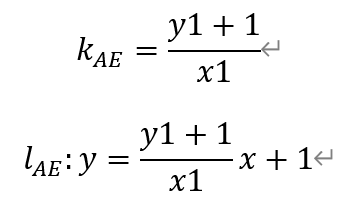
令x=3，解得，

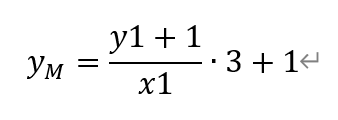
即有

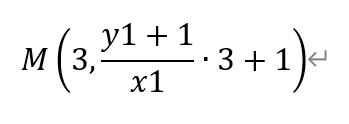
同理，可得点N的坐标为，

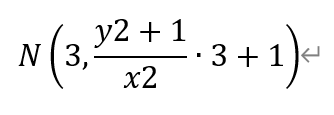
点M和点N之间的距离为，

其中，

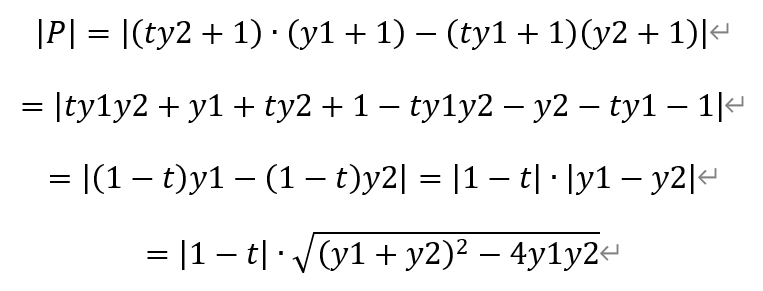
将前述y1+y2和y1y2代入，有

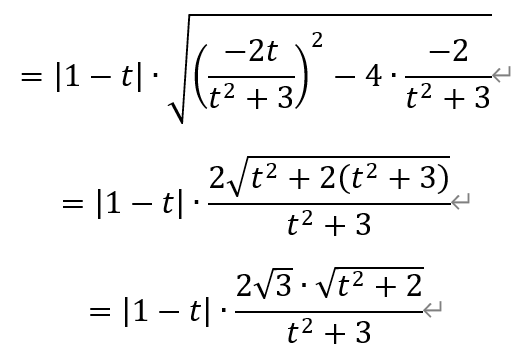
以及

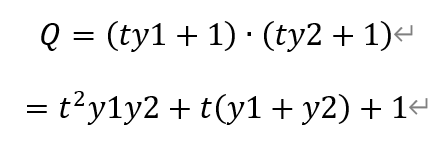
将前述y1+y2和y1y2代入，有

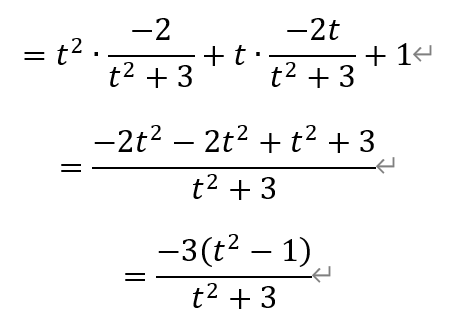
代回|MN|的表达式，有

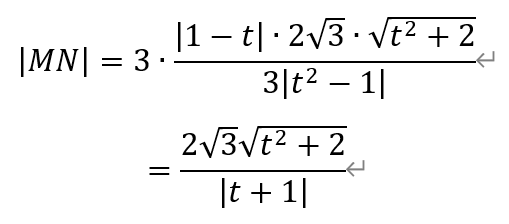
于是，△AMN的面积为，

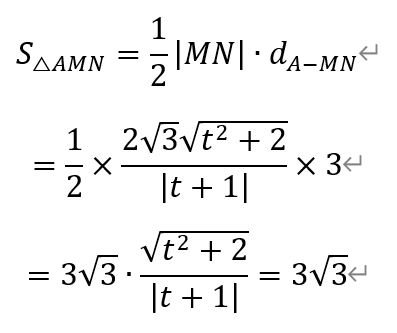
解得，

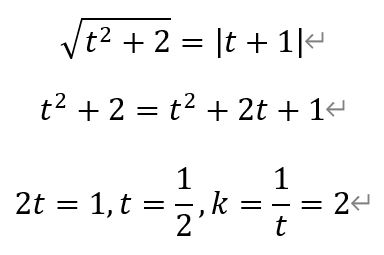
即k=2。

 

综上，k的取值为0或2。