CSP-S模拟试题及参考答案
-
-
梁老师 北京小升初老师～
0 人点赞了该文章 · 85 浏览
1.以下关于CSP-J/S的描述错误的是() 分值2分
A.任何人都可以自愿报名参加CSP-J/S
B.CSP-J/S是CCF独立主办的认证，和任何其他机构主办的等级考试无关
C.CSP-J/S和NOIP有密切关系
D.CSP-J/S认证成绩优异者，可参加NOI省级选拔，省级选拔成绩优异者可参加NOIC
2.-128的补码表示为()分值2分
A.00000000
B.00000001
C.10000000
D.11111111
3.以下不属于TCP拥塞控制算法的是() 分值2分
A.慢启动
B.拥塞避免
C.快启动
D.快速重传
4.以下不是基于UDP协议的是() 分值2分
A.DNS
B.RIP
C.TELNET
D.TFTP
5.定义如下函数add_edge和全局变量：
int to[MAX],nxt[MAX],h[MAX],top;
void add_edge(int u,int v){
to[++top]=v,nxt[top]=h[u],h[u]=top;
}
如下图节点编号从1开始，按边的编号顺序，以前向星的方式存储，请问nxt[h[3]]的值为()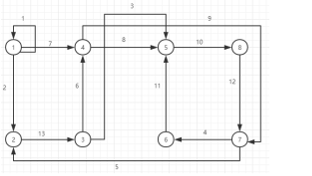
分值2分
A.6
B.3
C.8
D.7
6.如下图所示，从节点1走6步走到节点5的方案数有多少种()
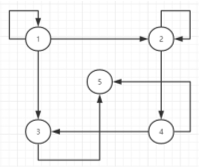
A.5
B.8
C.7
D.6
7.同时查找 2n 个数中的最大值和最小值，最少比较次数为( )。 分值2分
A.3(n-2)/2
B.3n-2
C.4n-2
D.2n-2
8.设 A 和 B 是两个长为 n 的有序数组，现在需要将 A 和 B 合并成一个排好序的 数组，请问任何以元素比较作为基本运算的归并算法最坏情况下至少要做 ( )次比较。 分值2分
A.n2
B.nlog2n
C.2n
D.2n-1
9.G 是一个非连通简单无向图，共有 36 条边，则该图至少有( )个顶点 分值2分
A.10
B.9
C.8
D.7
10.由四个不同的点构成的简单无向连通图的个数是( ) 分值2分
A.32
B.35
C.38
D.31
11.前缀表达式- + * 4 + 2 3 1 5的值为() 分值2分
A.16
B.17
C.19
D.15
12.2+3*(4-(5+6))/7的逆波兰表达式为() 分值2分
A.2 3 4 5 6 - + * 7 / +
B.2 3 4 5 6 - + * / 7 +
C.2 3 4 5 6 + - * 7 / +
D.2 3 4 5 6 + + * / 7 -
13.若某算法的计算时间表示为递推关系：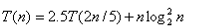
则该算法的复杂度为() 分值2分
A.O(n)
B.O(nlog2n)
C.O(nlog22n)
D.O(nlong23n)
14.若某算法的计算时间表示为递推关系：T(n)=3T(n/4)+nlong2n则该算法的复杂度为() 分值2分
A.O(n)
B.O(nlog2n)
C.O(nlog22n)
D.O(nlong23n)
15. 现有变量a,b,c,d，取值范围均为[0,15]，假设每个值出现的概率相同，则表达式的值能被3整除的概率( )(为计算机中的异或运算符，结果用分数形式表达) 分值2分
A．3/8
B.1/2
C.1/4
D.1/8
二、阅读程序写结果(共4题，每题10分，共计40分)
1.#include
using namespace std;
int a,b,c;
int* cal(int *p,int &q,int r) {
q+=r;
*p+=q;
return p;
}
int main() {
cin>>a>>b>>c;
c=*cal(&a,b,c);
cout<<a<<" span=""></a<<">
}
1.1 cal函数中参数p使用指针传递，q和r则是值传递 分值2.5分
对
错
1.2 cal函数返回一个指向int类型存储空间的地址 分值2.5分
对
错
1.3 当输入1 2 3时，程序输出结果为() 分值2.5分
A.6 2 3
B.6 5 3
C.6 5 6
D.1 2 6
1.4 当输入23 45 11时，程序的输出结果为() 分值2.5分
A.79 56 11
B.79 56 79
C.44 56 79
D.79 56 44
2.#include
#include
#define MAX 1000
#define p sqrt(3)
using namespace std;
int n,dp[1000][3];
int h0=1,h1=3;
double ans1=(2+p)/(2*p),ans2=(-2+p)/(2*p);
int main() {
cin>>n;
dp[1][0]=dp[1][1]=dp[1][2]=1;
for(int i=2,tmp; i<=n; i++) {
dp[i][0]=dp[i-1][1]+dp[i-1][2];
dp[i][1]=dp[i-1][0]+dp[i-1][1]+dp[i-1][2];
dp[i][2]=dp[i-1][0]+dp[i-1][1]+dp[i-1][2];
tmp=h1;
h1=2*(h1+h0);
h0=tmp;
}
for(int i=1; i<=n; i++) {
ans1=ans1*(1+p);
ans2=ans2*(1-p);
}
cout<<h1<<endl;< span=""></h1<<endl;<>
cout<<dp[n][0]+dp[n][1]+dp[n][2]<<endl;< span=""></dp[n][0]+dp[n][1]+dp[n][2]<<endl;<>
cout<<ans1+ans2<<endl;< span=""></ans1+ans2<<endl;<>
}
2.1 上述程序的输出中h1和dp[n][0]+dp[n][1]+dp[n][2]的值相等 分值2.5分
对
错
2.2 上述程序的输出中dp[n][0]+dp[n][1]+dp[n][2]和ans1+ans2的值相等 分值2.5分
对
错
2.3 当n等于5时，第一行输出(即h1)结果为( ) 分值2.5分
A.164
B.60
C.448
D.128
当n等于10时，第三行输出(即ans1+ans2)结果为() 分值2.5分
A.9136
B.68192
C.24960
D.3344
3.#include
#include
#define LL long long
using namespace std;
LL l,r;
LL f[12][10][10][2][2][2],a[20];
LL Dfs(LL now,LL p,LL pp,LL _4,LL _8,LL top,LL hw) {
if(_4&&_8) return 0;
if(!now) return hw;
if(!top && f[now][p][pp][_4][_8][hw]!=-1) return f[now][p][pp][_4][_8][hw];
LL Up=top?a[now]:9;
LL ret(0);
for(LL i=0; i<=Up; ++i)
ret+=Dfs(now-1,i,p, _4|(i==4),_8|(i==8), top&&(i==Up) ,hw|(i==pp&&i==p));
if(!top) f[now][p][pp][_4][_8][hw]=ret;
return ret;
}
inline LL Solve(LL x) {
LL tot(0);
while(x) {
a[++tot]=x;
x/=10;
}
if(tot!=11) return 0;
LL ret(0);
for(LL i=1; i<=a[tot]; ++i)
ret+=Dfs(tot-1,i,0,(i==4),(i==8),i==a[tot],0);
return ret;
}
int main() {
cin>>l>>r;
memset(f,-1,sizeof(f));
cout<<solve(r)-solve(l-1);< span=""></solve(r)-solve(l-1);<>
return 0;
}
3.1 同时包含4和8的数字都不会被统计 分值2.5分
对
错
3.2 相邻数位中，超过3个数位相同的数字都不会被统计 分值2.5分
对
错
3.3 下列哪个是合法(会被统计)的数字() 分值2.5分
A.2323234823
B.1015400080
C.23333333333
D.10010012022
3.4当输入12121284000 12121285550时，程序输出结果为() 分值2.5分
A.5
B.457
C.455
D.6
4.
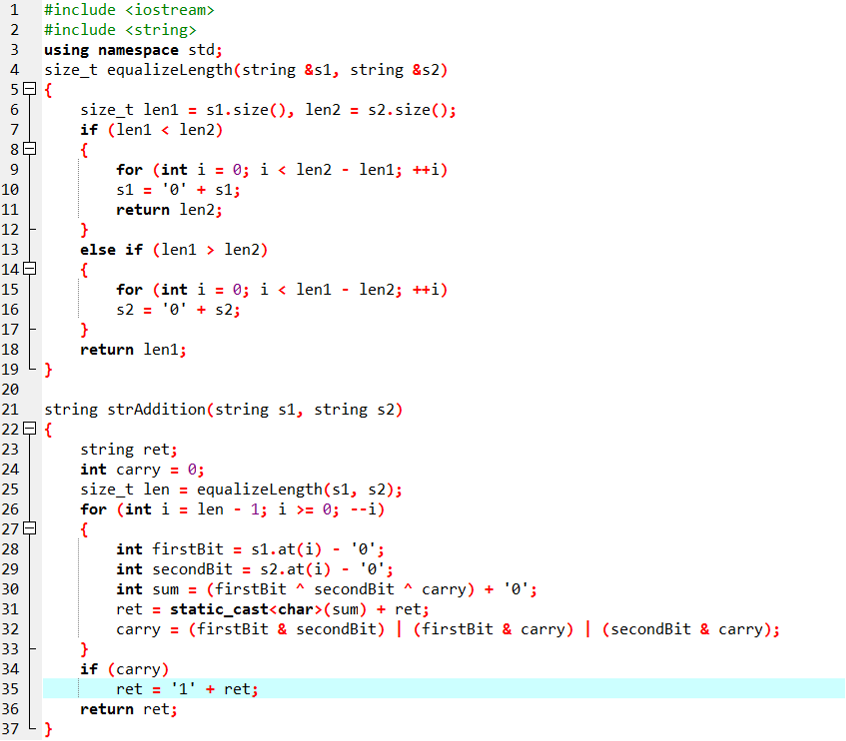
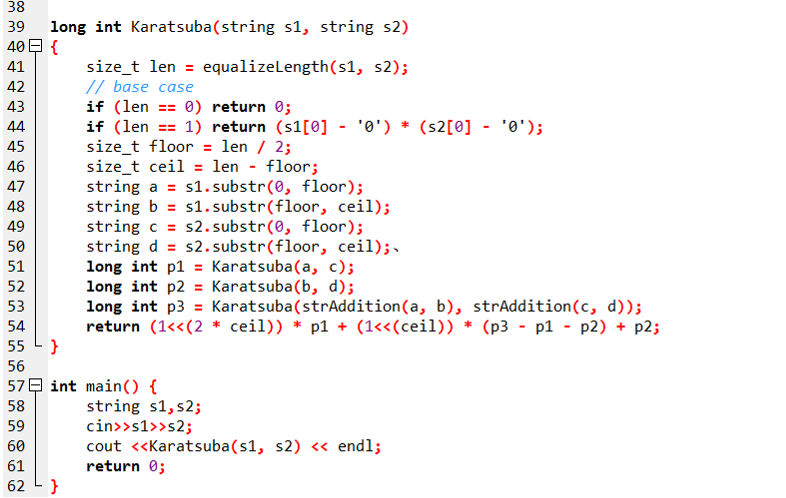
4.1 上述程序实现大整数加法 分值2.5分
对
错
4.2 上述程序的算法复杂度大于（其中n为max(s1.length(),s2.length())） 分值2.5分
对
错
4.3 当输入111 011时程序输出为() 分值2.5分
A.10
B.4
C.21
D.2
4.4 当输入10101 101010时程序输出为() 分值2.5分
A.441
B.882
C.1764
D.220
五、完善程序(每题15分，共计30分)
1.（链表反转）单向链表反转是一道经典算法问题，比如有一个链表是这样的，1->2->3->4->5，反转后成为 5->4->3->2->1。现给定如下链表节点的定义：
struct LinkNode{
int value;
LinkNode* next;};
非递归实现：
LinkNode* Reverse(LinkNode* header) {
if (header == NULL || header->next == NULL) {
return header;
}
LinkNode* pre = header, *cur = header->next;
pre->next = NULL;
while(cur != NULL) {
LinkNode* next = ____1____;
___2____ = pre;
pre = cur;
cur = next;
}
return pre;
}
递归实现：
LinkNode * Reverse(LinkNode * head) {
if (head == NULL || head->next == NULL) {
return head;
}
LinkNode * newhead = ___3____;
___4_____ = head;
head->next = ___5____;
return newhead;
}
1.1上述程序___1___中应该填写()
分值3分
A.pre-> next
B.cur-> next
C.header-> next
D.NULL
1.2上述程序___2___中应该填写() 分值3分
A.pre-> next
B.cur-> next
C.header-> next
D.NULL
1.3上述程序___3___中应该填写() 分值3分
A.ReverseList(head)
B.ReverseList(pre)
C.ReverseList(cur)
D.ReverseList(head->next)
1.4上述程序___4___中应该填写() 分值3分
A.pre-> next->next
B.cur-> next->next
C.header-> next->next
D.NULL
1.5上述程序___5___中应该填写() 分值3分
A.pre-> next
B.cur-> next
C.header-> next
D.NULL
2) (最小环问题)给定一张无向图，求图中一个至少包含 3 个点的环，环上的节点不重复，并且环上的边的长度之和最小。该问题称为无向图的最小环问题。在本题中，你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。若无解，输出 No。
1.1上述程序___1___中应该填写（） 分值3分
A.j
B.pos[i][j]
C.i
D.pos[j][i]
1.2上述程序___2___中应该填写() 分值3分
A.j
B.pos[i][j]
C.i
D.pos[j][i]
1.3上述程序___3___中应该填写() 分值3分
A.D[i][j]+G[k][j]+G[i][k]
B.D[i][j]+G[j][k]+G[k][i]
C.D[i][k]+G[k][j]+G[i][j]
D.D[i][j]+G[j][i]+G[i][k]
1.4上述程序___4___中应该填写() 分值3分
A.D[k][j]>D[i][k]+D[k][j]
B.D[i][j]>D[i][k]+D[k][j]
C.D[i][j]<d[i][k]+d[k][j]< span=""></d[i][k]+d[k][j]<>
D.D[i][k]>D[i][k]+D[k][j]
1.5上述程序___5___中应该填写() 分值3分
A.pos[i][i]
B.stk[i]
C.pos[1][i]
D.pos[i][1]
参考答案
1C 2C 3C 4C 5B 6B 7B 8D 9A 10C
11A 12C 13D 14B 15A
阅读1错对CB
2 对对AC
3对错CA
4错错CB
完善程序
1B 2B 3D 4C 5D
1B2A3B4B5B
全部 0条评论