一、选择题（本大题共10小题，每小题5分，共50分。在每小题列出的四个选项中，选出符合题目要求的一项）

1.点(1,1)到直线x-y+1=0的距离是（  ）。

A)1/2    B)√2/2   C)1    D)√2

 

[答案]B

 

[解析]利用点到直线的距离公式，有

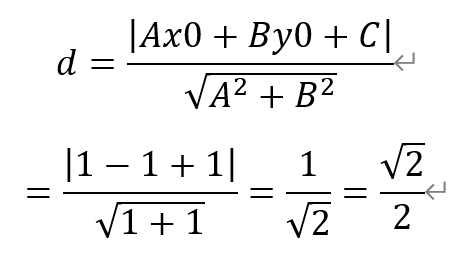
即值为√2/2。故选B。

 

2.-2与-8的等差中项是（  ）。

A)-5    B)-4   C)4    D)5

 

[答案]A

 

[解析]根据等差中项的性质，有

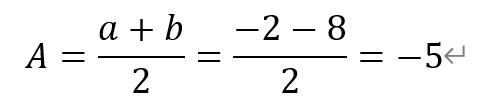
即值为-5。故选A。

 

3.已知直线l过点(0,1)，且与直线x-2y+2=0垂直，则直线l的方程是（  ）。

A)x+2y+1=0    B)2x+y+1=0

C)x+2y-1=0    D)2x+y-1=0

 

[答案]D

 

[解析]根据两条直线平行的性质，设直线l的方程为：2x+y+c=0。将点(0,1)代入，得

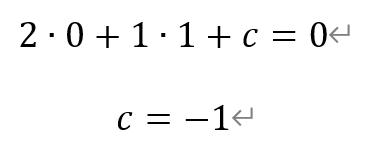
即直线l的方程为2x+y-1=0。故选D。

 

4.已知函数f(x)=lnx/x，则f′(x)=（ ）。

A)(1-lnx)/x²    B)(1+lnx)/x²    C)(lnx+1)/x    D)(lnx-1)/x

 

[答案]A

 

[解析]函数f(x)的定义域为x＞0。

对函数f(x)求导，得

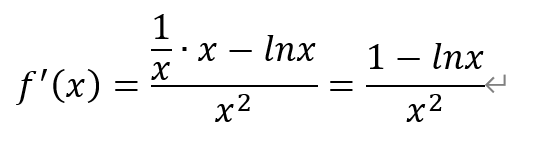
即导函数为(1-lnx)/x²。故选A。

 

5.已知圆x²+y²=1与圆(x-3)²+(y-4)²=r²(r＞0)外切，则r=（  ）。

A)1    B)2   C)3    D)4

 

[答案]D

 

[解析]单位圆O1的圆心为(0,0)，半径为1。圆O2的圆心为(3,4)，半径为r。两圆的圆心距|O1O2|=5，因此r=5-1=4。故选D。

 

6.曲线f(x)=x²e^x在点(1,f(1))处的切线方程为（  ）。

A)ex-y=0    B)2ex-y-e=0

C)3ex-y-2e=0    D)4ex-y-3e=0

 

[答案]C

 

[解析]函数f(x)的定义域为R。

对函数f(x)求导，得

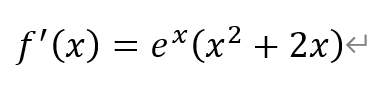
于是，有

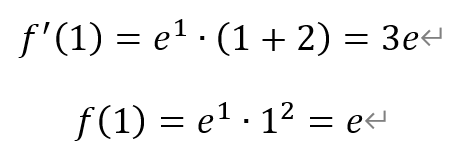
因此函数f(x)在点(1,f(1))处的切线方程为，

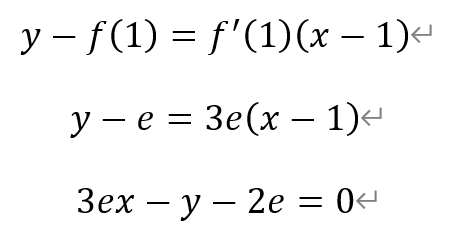
即方程为3ex-y-2e=0。故选C。

 

7.已知等比数列{an}的公比为q，a1＜0，则“q＞1”是“{an}为递减数列”的（  ）。

A)充分不必要条件    B)必要不充分条件

C)充分必要条件    D)既不充分也不必要条件

 

[答案]C

 

[解析]根据等比数列的通项公式，

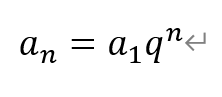
当a1＜0时，若q＞1，则an单调递减。因此，“q＞1”是“{an}为递减数列”的充要条件。

 

[注释]本题完整的知识点为：若a1＞0，q＞1，an单调递增；0＜q＜1，an单调递减。若a1＜0，q＞1，an单调递减；0＜q＜1，an单调递增。若q＜0，数列{an}为摆动数列，an不具有单调性；若q=1，数列{an}为常数列。

 

8.点M是正方体ABCD-A1B1C1D1的底面ABCD内（包括边界）的动点．给出下列三个结论：

① 满足D1M∥BC1的点M有且只有1个；

② 满足D1M⊥B1C的点M有且只有1个；

③ 满足D1M∥平面A1B1C1的点M的轨迹是线段．

则上述结论正确的个数是（  ）。

A)0    B)1    C)2   D)3

 

[答案]C

 

[解析]连接A1BC1和ACD1，如图所示。

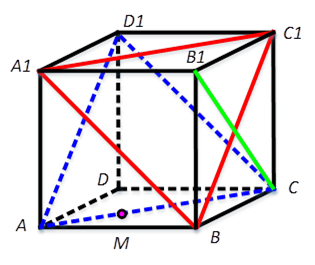
显然面A1BC1∥面ACD1，所以选项①和③正确。在底面ABCD上不存在点M，使得D1M⊥B1C，因此选项②错误。故正确的结论个数为2个，选C。

 

9.已知A,B是圆C：x²+y²=1上的两点，P是直线x-y+m=0上一点，若存在点A,B,P，使得PA⊥PB，则实数m的取值范围是（ ）。

A)[-1,1]    B)[-2,2]   C)[-√2,√2]   D)[-2√2,2√2]

 

[答案]B

 

[解析]如图所示。点A(1,0)，点B(0,-1)分别为单位圆上的点。

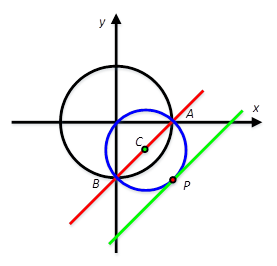
以直线AB为直径作圆，与直线y=x+m交于点P，则PA⊥PB。点C(1/2,-1/2)到该直线的距离等于半径√2/2，即

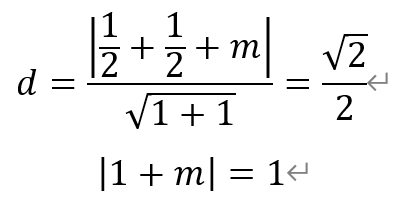
解得，m=0(舍)或者-2。同理，可求得m的最大值为2。因此m的取值范围为[-2,2]。故选B。

 

10.北京大兴国际机场的显著特点之一是各种弯曲空间的运用，在数学上用曲率刻画空间弯曲性．规定：多面体的顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角，角度用弧度制)，多面体面上非顶点的曲率均为零，多面体的总曲率等于该多面体各顶点的曲率之和．例如：正四面体在每个顶点有3个面角，每个面角是π/3，所以正四面体在每个顶点的曲率为2π-3×π/3=π，故其总曲率为4π．给出下列三个结论：

① 正方体在每个顶点的曲率均为π/2；

② 任意四棱锥的总曲率均为4π；

③ 若某类多面体的顶点数V，棱数E，面数F满足V-E+F=2，则该类多面体的总曲率是常数．

其中，所有正确结论的序号是（ ）。

A)①②    B)①③    C)②③    D)①②③

 

[答案]D

 

[解析]根据题意，正方体在每个顶点连接三个面，每个面角都是π/2。因此，每个顶点的曲率为2π-3×π/2=π/2。因此，选项①正确。

 

关于选项②和③的讨论，具体参见2021年1月的八省联考第20题。

 

二、填空题（本大题共6小题，每小题5分，共30分）

11.设函数f(x)=sinx，则f′(-π/4)=        ．

 

[答案]√2/2

 

[解析]函数f(x)的导函数为f′(x)=cosx。于是有，

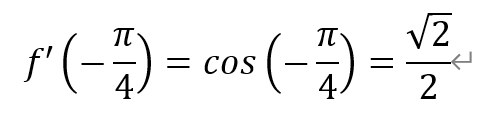
即值为√2/2。故填入√2/2。

 

12.已知抛物线的焦点到准线的距离为1，则抛物线的标准方程为        ．（写出一个即可）

 

[答案]y²=2x。（答案不唯一）

 

[解析]根据抛物线标准方程中p的几何意义，为焦点到准线的距离，即p=1。具体可以写出四种形式的方程，下略。

 

13.日常生活中的饮用水通常是经过净化的．随着水的纯净度的提高，所需净化费用不断増加．己知将1吨水净化到纯净度为x%时所需费用（单位：元）为

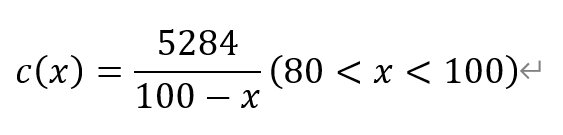
则净化到纯净度为99%时所需费用的瞬时变化率是净化到纯净度为95%时所需费用的瞬时变化率的        倍，这说明，水的纯净度越高，净化费用增加的速度越        (填“快”或“慢”)．

 

[答案]25；快。

 

[解析]对函数c(x)求导，得

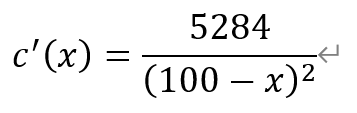
于是，

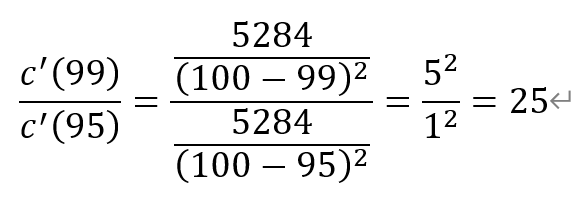
即净化到纯净度为99%时所需费用的瞬时变化率是净化到纯净度为95%时所需费用的瞬时变化率的25倍。

函数c(x)的导函数c′(x)单调递增，因此水的纯净度越高，净化费用增加的速度越快。

综上，填入25和“快”。

 

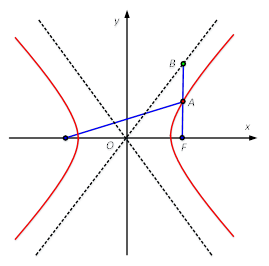
14.已知双曲线

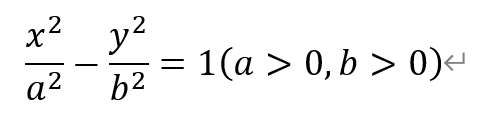
的右焦点为F，过点F作x轴的垂线l，l在第一象限与双曲线及其渐近线分别交于A,B两点．若FA=AB，则双曲线的离心率为        ．

 

[答案]2√3/3

 

[解析]如图所示。右焦点的坐标F(c,0)。渐近线的方程y=b/ax，将x=c代入，得

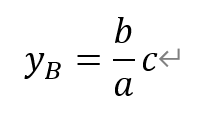
即点B(c,bc/a)。

将x=c代入双曲线的方程，有

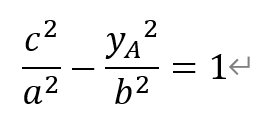
解得

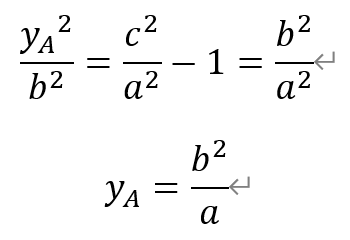
即点A(c,b²/a)。

由于FA=AB，所以

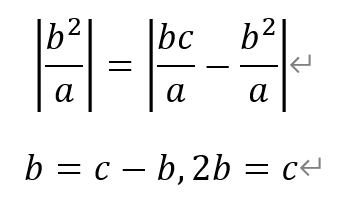
从而有，

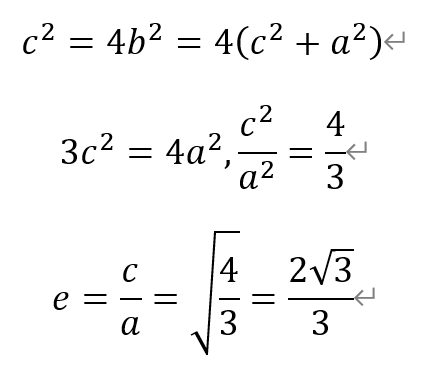
即值为2√3/3。故填入2√3/3。

 

15.已知数列{an}的前n项和为Sn，Sn=2an+n(n∈N^*)，则a1=        ，an=        ．

 

[答案]-1；1-2ⁿ,n∈N^*。

 

[解析]当n=1时，有

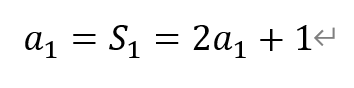
解得，a1=-1。

当n≥2时，有

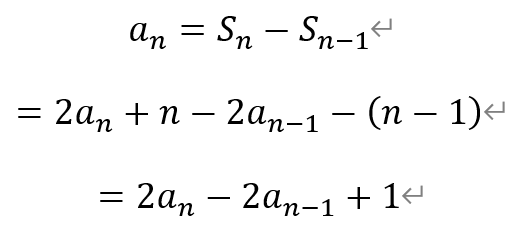
整理得，

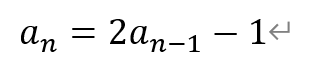
利用待定系数法，设存在实数m，使得下式成立

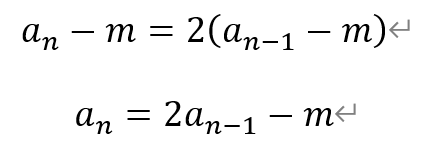
比较系数，得m=1。于是有，

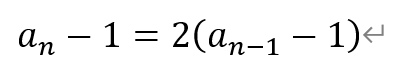
从而，数列{an-1}为公比为2的等比数列，首项为a1-1=-2。即

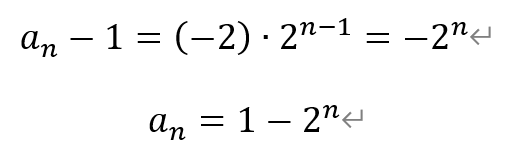
其中，n∈N^*。

综上，填入-1和1-2ⁿ。

 

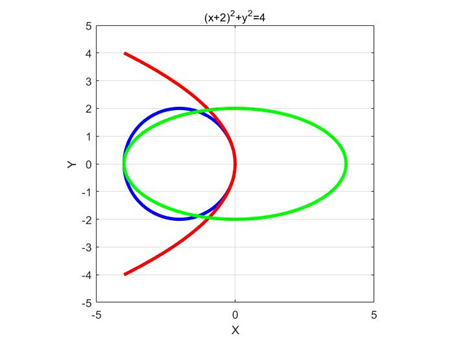
16.古希腊数学家阿波罗尼斯发现：平面内到两个定点A,B的距离之比为定值λ(λ≠1)的点的轨迹是圆．人们将这个圆称为阿波罗尼斯圆，简称阿氏圆．已知点A(-1,0)，B(2,0)，动点M满足|MA|/|MB|=1/2，记动点M的轨迹为曲线W，给出下列四个结论：

① 曲线W的方程为(x+2)²+y²=4；

②曲线W上存在点D，使得D到点(1,1)的距离为6；

③曲线W上存在点E，使得E到点A的距离大于到直线x=1的距离；

④ 曲线W上存在点F，使得F到点B与点(-2,0)的距离之和为8．

其中所有正确结论的序号是        ．

 

[答案]①④

 

[解析]关于选项①：设点M(x,y)。根据阿氏圆的定义，有

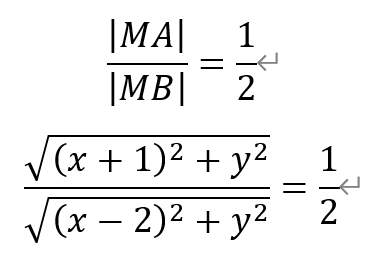
整理并化简得，

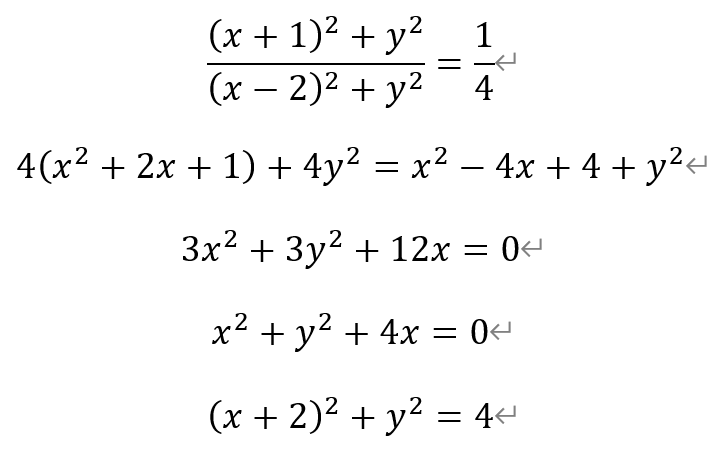
因此，选项①正确。

 

关于选项②：由①可得，该阿氏圆W的圆心为M(-2,0)，半径为2。

则M到N(1,1)的距离为，

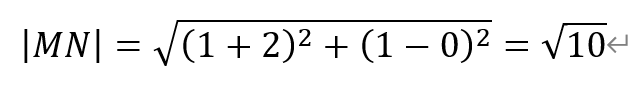
于是，W上的点到点N距离的最大值为，

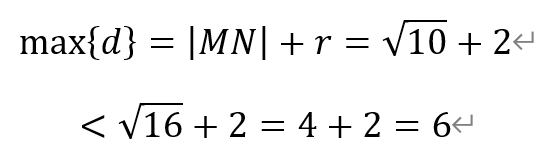
即圆W上到点N(1,1)的距离为6的点不存在。因此，选项②错误。

 

关于选项③：由于点A(-1,0)，根据抛物线的性质，到点A的距离等于到定直线x=1的距离相等的点的轨迹为抛物线，其方程为，

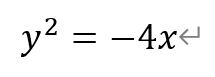
它与圆W的交点为坐标原点。即在W上不存在到定点A的距离大于到定直线x=1的点。因此，选项③错误。

 

关于选项④：设点P(-2,0)。根据椭圆的定义，到点B(2,0)与到点P的距离之和为8的点的轨迹为椭圆，且2a=8，2c=4。即a=4，c=2。由于a＞c，所以该椭圆存在。因此，选项④正确。

综上，选项①④正确，选项②③错误。故填入①④。