概念介绍

非：not  ¬   与：and ∧    或：or  ∨     异或：xor ⊕

运算级比较

括号  >  非  >  与  >  或、异或 (or和xor是同级的)

如果加入加减乘除，就是以下这样：

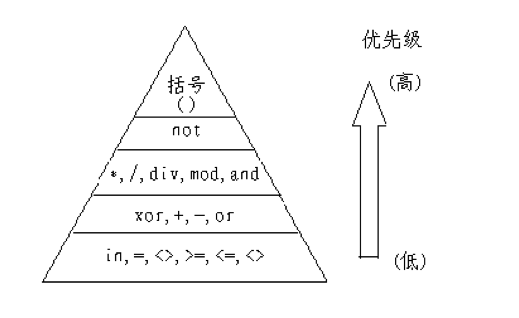
注意：同级的运算符不分高低，计算时按照从左到右运算。

例题1．若A=True，B=False，C=True，D=False，以下逻辑运算表达式真的有( )。

A．(A∧B)∨(C∧D∨¬A） B．((¬A∧B)∨C)∧¬B

C．(B∨C∨D)∨D∧A       D．A∧(D∨¬C)∧B

题解：一个个算结果，比如A选项(A∧B)∨(C∧D∨¬A) ，根据运算级的比较，我们可以定下运算的顺序，然后按运算顺序计算结果。注意，这类题是有个小技巧的。比如A选项可以先看中间的∨，为什么呢？因为∨的左右有一边是真就行，可以不去看另外一边。

A选项的结果是：(A∧B)∨(C∧D∨¬A)，(A∧B)=假，(C∧D∨¬A)中C∧D =假，¬A=假，所以(C∧D ∨¬A)=假。于是A选项可以简写为：假∨（假 ∨假）= 假。

B选项的结果是：((¬A∧B)∨C)∧¬B，如果¬B是假那么就可以不去看前面的((¬A∧B)∨C)，可惜的是¬B是真，那么就要看((¬A∧B)∨C)，发现C是真，所以不看(¬A∧B)，于是B选项可以简写为：(？∨真)∧真=真。

C选项的结果是：（B∨C∨D）∨D∧A ，D∧A=假，所以不得不看前面部分（B∨C∨D），只要BCD有一个是真，那么（B∨C∨D）=真，而容易发现C=true。所以C选项可以简写为：真∨ 假 = 真。

D选项的结果是：A∧(D∨¬C)∧B，我们很容易发现D选项的特殊结构为 ？∧？∧？，三个？有一个是假，那么D为假，A和B不用计算便可看出，所以先发现B=假，所以D=假。

例题2．计算23 +2 or 2 and 5 * 3 - 6 xor 5=(  )。

题解：数字也有逻辑运算，当然也可以混合加减乘除。

这里举例说明运算的操作：

---

往年真题

1. 以下逻辑表达式的值恒为真的是( )

  A．P∨(¬P∧Q)∨(¬P∧¬Q)

  B．Q∨(¬P∧Q)∨(P∧¬Q)

  C．P∨Q∨(P∧¬Q)∨(¬P∧Q)

  D．P∨¬Q∨(P∧¬Q)∨(¬P∧¬Q)

2. 若A=True，B=False，C=True，D=False，以下逻辑运算表达式真的有(  )

   A．(A∧B)∨(C∧D∨¬A)    B．((¬A∧B)∨C)∧¬B

   C．(B∨C∨D)∨D∧A         D．A∧(D∨¬C)∧B

3. 设A=true，B=false，C=true，D=false，以下逻辑运算表达式值为真的是(  )

 A. (A∧B)∨(C∧D∨A)           B. ((A∧B)∨C)∧D

 C. (B∨C∨D)∧D∧A               D. A∧(D∨C)∧B

4. 当(A>=B) and (B>=C)的取值为true时，那么表达式(A>C) or (B=C)的取值为(  )

   A． True     B． False     C． 无法判断  

   D． 只有当ABC三个数都为正数时才为true 

   E． 只有当ABC三个数都为正数时才为false 

5. 设A=B=true，C=D=false，以下逻辑运算表达式为真的有(  )

    A.  (A∧B)∨(C∧D∨A)           B. ((A∧B)∨C)∧D

C.  A∧(B∨C∨D)∨D             D.  A∧(D∨C)∧B

6. 命题“P→Q”可读做P蕴涵Q，其中P、Q是两个独立的命题。只有当命题P成立而命题Q不成立时，命题“P→Q”的值为false，其他情况均为true。与命题“P→Q”等价的逻辑关系式是(  )

    A. P∨Q        B.  P∧Q         C. (P∨Q)       D.  (Q∧P)  

7. 设A=B=True，C=D=False，一下逻辑运算表达式值为假的有(  )

   A．(¬A∧B)∨(C∧D∨A)  B．¬(((A∧B)∨C)∧D)  

   C．A∧(B∨C∨D)∨D       D．(A∧(D∨C))∧B

8. 设A=B=D=true，C=E=false，以下逻辑运算表达式值为真的有(  )

   A. (A∧B)∨(C∧D)∨E        B. (((A∧B)∨C)∧D∧E)

   C. A∧(B∨C∨D∨E)          D. (A∧(B∨C)) ∧D∧E

9. 设全集I = {a, b, c, d, e, f, g, h}，集合  BA = {a, b, c,d, e, f}，AC  = {c, d, e}，BA= {a, d}，那么集合  CBA为(  )

   A.{c, e}      B. {d, e}      C. {e}      D. {c, d, e}    E. {d, f}

10. 设全集I = {a, b, c, d, e, f, g}，集合A = {a, b, c}，B = {b, d, e}，C = {e, f, g}，那么集合为( )

   A. {a, b, c, d}    B. {a, b, d, e}   C. {b, d, e}     D. {b, c, d, e}    E. {d, f, g}

1A 2BC 3B 4A 5AC 6AD 7D 8AC 9A 10A