
一.填空题Ⅰ(每小题8分,共32分)
1. 算式 (2021+20-21)÷20×21的计算结果是_________.
〖答案〗2121
〖考点〗四则运算
2. 小明、小华和小亮各有一些零用钱.小明与小华的零用钱共有20元,小华和小亮的零用钱共有25元,且小亮的零用钱是小明的2倍.那么小华的零用钱有_________元.
〖答案〗15
〖考点〗等量代换
小明+小华=20
小亮是2个小明
所以小华+2个小明=25
两者对比,差了一个小明即5块
所以小华:20-5=15
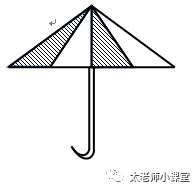
3. 下图是一个漂亮的中国传统油纸伞图案,在这个图案中,包含阴影的三角形共有_________个.
4.一个边长为整数的正方形,它的周长与面积的数值之和为2021,那么这个正方形的边长是_________.那么只有43*47尾数符合三七二十一,验证一下即可
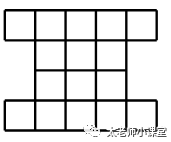
5. 下图为一个地区的军事布局图,现在要在格子中布置一些大炮,要求每个格子中最多布置一门大炮,任意两个布置大炮的格子不能有边相邻,那么最多可以布置_________门大炮.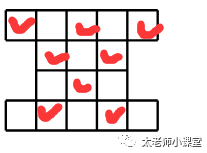
6. 熊大和熊二为了阻止光头强偷摘香蕉,至少会有一个在森林里巡逻.如果熊大单独巡逻,光头强1分钟能摘8个香蕉;如果熊二单独巡逻,光头强1分钟能摘10个香蕉;如果熊大和熊二一起巡逻,光头强1分钟只能摘4个香蕉.现在光头强在12分钟内共摘了88个香蕉.已知在光头强偷摘香蕉期间,熊大巡逻的时间是熊二巡逻时间的2倍,那么熊大共巡逻了_________分钟.如果共同巡逻3分钟,则熊大单独巡逻7分钟,熊二单独巡逻2分钟7. 如图,10个完全相同的正五边形边与边拼接在一起,可以在中间围出一个正十边形.3个完全相同的正n边形边与边拼接在一起,可以在中间围出一个正三角形,那么n的值是_________.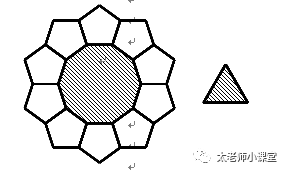
如果想要拼接上,能够围上,那么两个图形就要凑够360°-60°=300°
8. 对69896这个五位数进行若干次操作,每次操作可将相邻的两位数旋转180度(如98进行一次操作后变为86, 96进行一次操作后还是96).那么经过有限次操作后可得到的最大的五位数是_________.可以尝试,会发现6总在①③⑤这三个位置,9总会在②④这两个位置9. 石老师将写有1、2、3、4的卡片各一张,分别发给甲、乙、丙、丁.然后发生了如下对话:
甲对乙说:你卡片上的数是4; 丁对甲说:你卡片上的数是1.
石老师发现:持有卡片数字奇偶性相同的人之间说的都是正确的,持有卡片数字奇偶性不同的人之间说的都是错误的,并且甲、丁卡片上的数字之和小于乙、丙卡片上的数字之和.
那么甲、乙、丙、丁卡片上数字依次连接组成的四位数是_________.1+2+3+4=10,乙和丙大于5,可以是2+4或者3+4
分类讨论如果他俩是2和4那么他俩之间的对话应该是正确的乙对丙说:你卡片上的数是3是错误的,所以丙是4乙是310. 如图,ABCD是一张正方形纸片,将纸片沿着CE对折,点D被折到点G的位置,再沿着CF对折纸片,将点B折到点G的位置.如果DE=18,BF=6,那么△AEF的面积是_________.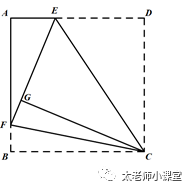
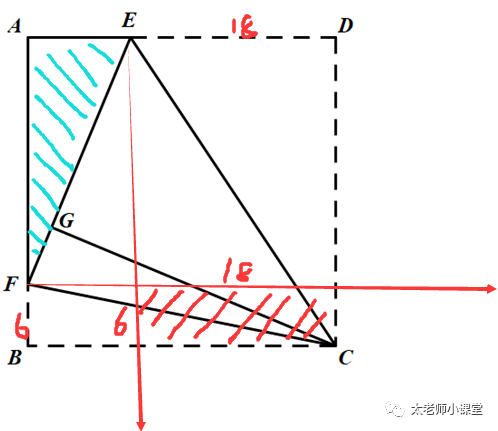
三角形CFE是正方形去掉红色之后的一半(等具体讲到一半模型这讲的时候我们再细说)考试技巧:这看到6和18,找到对应的面积(红色),和所求(蓝色)一对比,看着差不多,直接答108就完事儿了,考试时间有限,猜的艺术可能帮助你在策略上领先一点
11.小聪玩一个三国集卡游戏,有曹操,刘备,孙权三种武将卡,每种武将卡都有一星、二星、三星这三个星级,三张同名称的低星级卡片可以合成一张同名称的高一星级卡片,一张高星级卡片可以分解成另两种低一星级的卡片各一张(比如:三个一星曹操可以合成一个二星曹操,一个三星曹操可以分解为一个二星孙权和一个二星刘备).已知小聪可以购买的卡片只有一星卡片,武将随机.那么小聪至少一次性购买_________张卡片,才能保证自己可以通过合成或者分解获得互不相同的三张三星卡片.考虑最倒霉的情况,小聪买的卡片全是曹操,那么,合成三星曹操需要3×3=9张卡,此时另外两个武将需要将二星曹操分解成为一星孙权和一星刘备,最终3张一星曹操变一张一星孙权和一张一星刘备,一共需要9张孙权和9张刘备,那么至少需要9×3=27张曹操但容易忽略一个问题就是36张曹操那么最终所有的卡都是正好的,没有浪费,所以这其实并不是最倒霉的最倒霉的情况是35张曹操的时候就差一点就能合成完毕,此时没有曹操了,有2张曹操被浪费了那么35张曹操对应应该能合成出一个3星曹操,8张1星刘备和8张1星孙权此时不给曹操卡了,给1张刘备(36),那么刘备就齐活了,然后第37张还拿刘备,刘备多1,曹操多2这里又有一个容易想错的地方,第38张考虑最倒霉的情况再拿一张刘备,等第39张的时候才能凑齐最后一张孙权然而实际上如果多两张刘备同时多两张曹操的时候,差的一张孙权就已经有了~~~~~有点像空瓶换酒,从原本准备好合成三星刘备的9张一星刘备中借一个出来,配上多备的两张刘备,升级二星再分解,得到1星曹操和1星孙权(孙权有了),再用多备的两张曹操加上刚得到的曹操,升级二星再分解,得到1星刘备(还回去)和1星孙权所以第38张不论拿刘备还是孙权都已经可以保证凑齐了










全部 0条评论