ymo广告

1、 如果

那么 x=（  ）。

「答案解析」

裂项求和。

由于：

所以，x=18。

2、三位数，其中，这样的数有（  ）个。

❞

「答案解析」

可以分类枚举。

1）最小数字为0的时候，只有9+9+0一种组合，共2种排列。

2）最小数字为1的时候，有1+8+9一种组合，共6种排列。

3）最小数字为2的时候，有2+7+9和2+8+8两种组合，共6+3=9种排列。

4）最小数字为3的时候，有3+6+9、3+7+8两种组合，共6x2=12种排列。

5）最小数字为4的时候，有4+5+9、4+6+8、4+7+7三种组合，共6x2+3=15种排列。

6）最小数字为5的时候，有5+5+8、5+6+7两种组合，共3+6=9种排列。

7）最小数字为6的时候，有6+6+6一种组合，共1种排列。

综上所述，一共有2+6+9+12+15+9+1=54个。

此类分类方法稍微麻烦了些，不过便于理解。

3、连续掷一枚骰子 3 次，三次点数之和为 13 的不同抛掷结果有（   ）种。

「答案解析」

方法同上，分类枚举。

1）最小点数为1时，有1+6+6一种组合，共3种排列结果。

2）最小点数为2时，有2+5+6一种组合，共6种排列结果。

3）最小点数为3时，有3+4+6和3+5+5两种组合，共6+3=9种排列结果。

4）最小点数为4时，有4+4+5一种组合，共3种排列结果。

综上所述，一共有3+6+9+3=21种结果。

4、一个四位数，每一位数字都是奇数，各个数位上的数字和为 16，这样的四位数一共有（           ）个。

「答案解析」

方法同上，分类枚举。

1）1+1+5+9，共种。

2）1+1+7+7，共种。

3）1+3+3+9，共种。

4）1+3+5+7，共种。

5）1+5+5+5，共种。

6）3+3+3+7，共种。

7）3+3+5+5，共6种

综上所述，一共种。

5、乘积：1022×1023×1024×1025×1026×……×2020×2021×2022 是一个多位数，这个多位数的尾部有（  ）个连续的零。

「答案解析」

本题就是求该多位数中含有多少个2x5，由于2的数量远远超过5，也就是求包含多少个5。

2022!中5的因素个数是：

1021!中5的因素个数是：

因此，乘积中的多位数尾部连续个0的个数就是：

末尾一共有250个连续的零。

或者这样想。

我们依次去除5，能整除的留下商，不能整除的丢弃。

第一轮就是5x205,5x206,...,5x404，共404-204=200个5。

第二轮就是5x41,5x42,...,5x80，共80-40=40个5。

第三轮就是5x9,5x10,...,5x16，共16-8=8个5。

第四轮就是5x2,5x3，共2个5。

累加起来也就是有250个。

可以参考：[数学]第30届YMO交流活动6年级初赛试题 第五题。

6、如图，四边形 ABCD 与四边形 ACEF 都是平行四边形，三角形 ABC 的面积是 23 平方厘米， 三角形 AFD 的面积是 12 平方厘米，那么三角形 CDE 的面积是（    ）平方厘米。

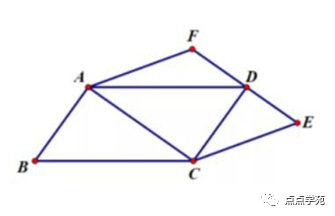
「答案解析」

这里用一半模型。

可以知道三角形CDE的面积加上AFD的面积就是23平方厘米。

三角形CDE的面积就是23-12=11平方厘米。

7、能被8整除，但不能被12整除的三位数共有(   )个。

「答案解析」

8和12的最小公倍数是24。

从1~999，8的倍数有[999/8]=124个，24的倍数有[1000/24]=41个。

从1~100，8的倍数有[100/8]=12个，24的倍数有[100/24]=4个。

因此，满足题意的三位数共有：

个。

8、把 2022 表示为若干个连续自然数的和，有（  ）种不同的表示方法。（注意：以 6＝1+2+3＝2+1+3 为例，这算是一种表示方法，它们只是加数的次序不同）

「答案解析」

先将2022分解，有：

我们依次拿18以内的质数去除，可以判断出337是质数。

考虑下连续自然数和的特性，只有如下几种：

504,505,506,507，

673,674,675，

163,164,..,168,169,...,173,174。

共三组。

9、计算：（   ）.

「答案解析」

这可以首尾用立方和公式，不过计算量比较大，也可以用连续的立方和公式。

也就是：

所以：

。

10、已知 a、b、c 都是质数,且 b-a=c-b=34，则 a+b+c=（   ）。

「答案解析」

质数一般都会牵涉到2，可惜这道不是。

从条件来看，只能知道a+c=2b和a

这个不好算，我们一般都背过100以内的质数表吧。

我们就拿最小的3去尝试，可以发现：

3,37,71是一组解。

对于大于3的质数，我们可以写成6x+1或6x-1的形式。

令a=6x-1,b=6y-1,c=6z-1，

1）对于6x-1

由于：

很明显，6x+33是3的倍数，6y-1不是3的倍数，无解。

2）对于6x+1

由于：

同理，无解。

因此，3,37,71是唯一解。

所以，所求结果是。