13. 某班共有30名学生去看电影，他们的学号依次为1,2,……,30；他们手中的电影票恰好为某排的1号，2号，……，30号．现在按如下要求将电影票发给这些同学：对于任意两人甲、乙，若甲的学号能被乙的学号整除，则甲的电影票号码也能被乙的电影票号码整除．那么电影票共有________种不同的发放方式．

〖答案〗48

2016年小高组决赛A卷

14. 将一个固定好的正方形分割成3个等腰三角形，有如图的4种不同方式；如果将一个固定好的正方形分割成4个等腰三角形，那么共有          种不同方式．

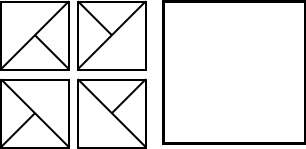
〖答案〗21

2017年小高组决赛A卷

12. 如图，有一个固定好的正方体框架，A、B两点各有一只电子跳蚤同时开始跳动．已知电子跳蚤速度相同，且每歩只能沿棱跳到相邻的顶点，两只电子跳蚤各跳了3歩，途中从未相遇的跳法共有________种．

〖答案〗343  

2018年小高组决赛A卷

10. 将右图中的8个小圆点涂成红色或黄色，要求每个点都至少与一个红点相邻（有线段或弧线直接相连的两个点称为相邻）．不同的涂法共有________种．

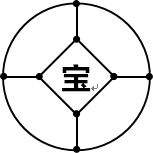
〖答案〗121

2019年小高组决赛A卷

8. 如果一个不小于10的自然数A的各位数字互不相同，且任意去掉A的一个数字后得到的数都是A的约数，则称A是“黄梅数”．例如：因为24、20、40都是240的约数，所以240是“黄梅数”．那么“黄梅数”一共有_______个．

〖答案〗10

点评：数学花园探秘小高组的计数问题属于难度大的考点之一。这类问题往往和数论等问题相结合，对于同学们的综合能力要求较高。

通过近五年的题目，我们可以总结出计数问题的两个最基本原理就是加法原理和乘法原理，一个最基本方法就是枚举法。即使很复杂的计数问题也可以用这两个基本原理和一个基本方法解决。学有余力的同学还可以通过排列组合来使部分问题简单化。

一般计数问题的解题方法是

第一步：先找到至少一种符合题意的方法或种类，然后对找到的方法或种类的性质进行研究，思考两个问题：1、为什么这种情况满足题意？2、还有什么其他情况也可以满足题意？

第二步：对题目中所要求的情况进行分类，分类的原则是尽量每一类中不要有重复的部分，或者重复的部分可以应用简单的容斥原理进行排除。

第三步：对每一类中的情况进行枚举或者通过乘法原理分步进行计算，在枚举的时候，一定要按照某种固定的顺序进行枚举，比如从小到大，从低位到高位，从简单到复杂，这样可以做到不重不漏。