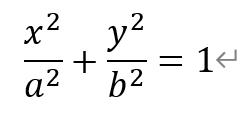文章 2022春节东西海三区学区看房指南

、本科率高于海淀、小升初拼zb的不少         东城特点：上限不高但下限不低、鸡娃氛围不太浓、大人孩子压力小、普高率和本科率不低、小升初相对来说 “公平”程度最高         三区多校划片执行差异：           & nbsp;     东城：2021多校划片随机性大，规律性弱，小学学位富裕情况下也可能调剂1911后生源        西城：2021多校划...

赞同0  93浏览  0评论 梁老师 2024-03-10 20:37

文章 提醒丨回户籍或房产小升初？涉及东西海朝四区申请流程和要求一览

京城四大区跨区升入初中校的相关细则。东城区 跨区入学一、申请办理方式及要求办理方式：登录“东城区义教入学服务系统”，上传相关证明、证件材料。上传材料要求：真实有效的材料原件照片或原件电子版。审核结果回 馈：家长在规定时间内提交相关材料，2-3个工作日内通过该系统反馈审核结果。二、相关材料及要求　(一)在本市外区就读的小学毕业生回东城区进行初中入学本市外区小学毕业生需由现就读小学在北京市初中入学服务平 台（https://hdqryjrx.bjedu.cn/）进行申请“回户口或家庭实际居住地所在区入学”操作后，方可进行申请回东城区升初中资格审核。1.小学毕业生户口和实际居住地在东城区需上传：(1)小...

赞同0  99浏览  0评论 梁老师 2024-03-10 20:43

文章 人大附早培、八少八素、小升初如何应对

，非京租房不占用房东指标，但是，一般房东可不这么想，不怕一万就怕万一。朝阳、东城说过630政策，海淀说过1911政策，政策之后的房子都属于多校，也就是买了有可能，但不是100%一定能去，但是如果不买就 一点希望都没有，对不对。入学顺位的说法，只针对于顶级学校比较明显，比如，我租房想去人大附小，这基本是没有可能的；但是我租房想去二外附小，这是没有问题的。顶级小学入学方式太多，房子只是其中一部分，这里就 不详细说了。东西朝海择校方向区别：海淀直升校太少，家长择校基本奔着顶级小学走，如人大附小、北大附小、中关村一二三、翠微、五一、七一、上地实验等，也有育英（万寿路校区）、理工附小这些。东城从2017年开...

北京小学

赞同0  197浏览  0评论 大语文教育 2024-03-10 20:48

文章 必看丨2021年北京这20所学校招收科技特长生！

等奖或东城区科技节比赛中荣获一等奖以上的应届毕业生。北京一六六中在2018年9月至2021年3月市科技节比赛中荣获市级一、二等奖或东城区科技节比赛中荣获一等奖以上的应届毕业生。北京二中基本要求：荣获3 9届、40届北京科技创新大赛三等奖及以上或北京市教育行政部门组织的科技比赛（以证书印鉴为准）二等奖及以上的学生。北京十五中电子技术、单片机、机器人要求市级比赛一等奖及以上，科技创新大赛、金鹏科技论坛要 求 市级一等奖以上；创客及人工智能类项目 要求市级比赛一等奖及以上；北京十八中其中一项要求科技特长生应具有较好的计算机基础知识，接受过机器人或航空模型相关知识的系统学习和训练，并在相关比赛中...

赞同0  131浏览  0评论 梁老师 2024-03-10 20:51

文章 你家的房子能用来上学吗？北京买房租房家庭都得看！

2022年幼升小的家长们注意啦！自己家旁边有心仪的小学，但您注意过您家的房产是否符合入学的要求吗？哪些房产是不能作为入学的房产呢？今天就为大家带来了北京各区的入学房产要求！心急的家长们赶快看过来吧~东 城区西城区海淀区朝阳区通州区丰台区石景山区昌平区...

赞同0  100浏览  0评论 梁老师 2024-03-10 20:55

文章 参考丨哪些高中招收艺术特长生？有什么特殊要求？

奖获得者。（3）东城区第21、22、23届学生艺术节集体项目展演中，一、二等奖获得者。（4）东城区第21、22、23届学生艺术节个人项目展演中，一、二等奖获得者。（5）东城区2018、2019、202 0年阳光少年艺术节展演中，一、二等奖获得者。（6）北京市2018、2019、2020年阳光少年艺术节展演中，一、二等奖获得者。（7）第十五届中国国际合唱节比赛评测A级合唱团的参演团员。（8）校外艺术单 位（少年宫）声乐、合唱优秀学员，学习满两年以上。（9）北京市知名青少年优秀合唱团体在团学生。（10）北京市金帆艺术团和市级艺术教育特色校的合唱团员。【说明】参加市级、区级艺术节的获奖证书仅限合唱集体项...

赞同0  115浏览  0评论 梁老师 2024-03-10 21:29

文章 年底请知晓！小学划片系统查询即将开启，居住地对应哪所小学一查便知！

2022年入学儿童或无法查询划片结果，建议大家可集中关注，往年入学查询系统一般在入学当年三月开放。各位家长注意，除通州区、丰台区有划片查询系统外，朝阳区、东城区同样有划片查询系统！看到这里肯定有不少家 长问，没有划片查询系统的城区该怎么看孩子的划片小学，京京也马上为您解答！通过小学招生简章查询方式其他城区目前暂未开放统一小学划片查询系统，满足单校划片入学的家长们可以通过居住地附近小学招生简章，查看自 家是否在学校招生范围内，提前对照整理小学招生相关材料。提醒：如您实际居住地点无划片学校，则需提前了解往年入学方式，将可能按照填报志愿或电脑派位进行登记报名（实际请以入学当年为准）。...

赞同0  125浏览  0评论 梁老师 2024-03-10 21:33

文章 二环内！东城最好的安定门交道口学区！永康胡同18号院如何？能否上方家胡同小学？

永康胡同18号院：东城安定门二手房，80年代的老小区，楼龄久，老旧小区改造后环境稍有改观，起码干净，还算整洁。社区不大，有3栋板楼，1号楼和2号楼南北朝向，3号楼东西朝向，1号楼是红砖楼，2号楼外墙粉 刷颜值好，3号楼青灰色。三栋楼中间有片空地，内有几棵树，还停了不少车（人车不分流），没有什么活动空间。社区无门禁，随便出入，管理不严格，绿化少，内部环境有待改善。三栋楼都是板楼，无电梯：1号楼，4个单 元，高6层，每单元每层2-3户。2号楼，3个单元，高6层，每单元每层2-3户。3号楼，6个单元，高6层，每单元每层2-3户。户型朝向面积：刚需的户型，改善的总价。64平南北两居，70平南北两居等等。优...

赞同0  130浏览  0评论 梁老师 2024-03-10 21:53

文章 北京各区学区制不断发展，100\%就近入学≠全民大派位

在北京小升初升学过程中，孩子们入学受学区划分影响较大，尤其西城、东城等区。那究竟学区制对小升初有哪些影响呢？今天，小编给大家来详细解惑一下。01学区划片分为划分首先，家长们需要知晓，学区在划分范围时一 般按照就近入学原则。就近入学的“就近”指的是相对就近，不是指绝对地理位置的远近，不是指某个学生的家庭住址距离某一所中学最近就能“就近入学”，也不是指某一所小学距离某一所中学近就是“就近入学”。教育部门 是根据适龄学生人数、学校分布、所在社区、学校规模、交通状况等因素，按照确保公平和就近入学原则依街道、路段、门牌号、村组等确定的划片范围，只能确定相对科学的划片规则，确保适龄儿童、少年整体相对就近入学。...

赞同0  78浏览  0评论 梁老师 2024-03-10 21:55

文章 年前得知道！2022年幼升小这些材料当下着急核对！每一项都不能拉下！

为准。持工作居住证需注意——据家长分享，海淀区持工作居住证租房幼升小需缴纳半年至一年的完税证明（不是所有城区都要求）；非京籍家长需注意——从2021年非京籍租房完税证明办理表可以看出，东城、西城、海淀 等入学要求租房至少一年以上，如果非京籍租房家长确定好入学城区的话，现在就可以开始准备了。04非京籍需房东协助材料非京籍需要房东协助的材料主要有：房东身份证、房产证、房东知情同意书（部分城区）从2021 年入学要求来看，租房提供的证件材料中有的需要房东协助，如果在开具完税发票时会要求房东身份证、房产证等，另外实行六年一学位的城区要求提供房东知情同意书，如果房东不同意租户使用该房产幼升小，租房非京籍将影...

赞同0  193浏览  0评论 梁老师 2024-03-10 22:13

文章 【须知】2022年非京籍入学家长社保是如何要求的？一方还是双方？

北京各区社保要求小编根据2021年相关要求整理了以下非京籍社保要求，赶紧一起来看看：提醒：从上图中可以看出大部分城区要求半年以上社保，并且至少一方在本区缴纳，东城区要求社保满一年，经济技术开发区和大兴 部分街道办，要求三年社保，因此对于2022及之后入学的家长，现在就要做好社保的核查工作啦！另外，2022年幼升小家长需要注意的是，石景山2021年政策中要求从2022年，双方需一年以上在京缴纳社保，租 房的需的话需在石景山区缴纳社保。...

赞同0  101浏览  0评论 梁老师 2024-03-10 22:17

文章 【速看】2022年幼升小各区线上审核部门是哪些？提前了解掌握！

整理，具体请以入学当年实际要求为准。东城区西城区海淀区朝阳区京京提醒：以上内容是京京根据2021年幼升小相关整理，2022年幼升小家长仅供各位家长参考，关于具体审核时间节点和材料要求，需等2022年政 策公布。...

赞同0  116浏览  0评论 梁老师 2024-03-10 22:21

文章 【趁早】2022年幼升小非京籍入学方式是怎样的？各区有所不同！

说明：目前2022年幼升小政策暂未出台，以下内容来源于各区2021年入学要求，大家可以参考准备，最终请以入学当年实际要求为准。东城区非本市户籍适龄儿童少年通过联审后，东城区教委将通过电脑派位的方式在东 城区内多校划片安排入学。西城区符合西城区入学条件的集体户籍、按本市户籍对待、非本市户籍等其他适龄儿童，在全区范围内按计划派位入学。派位结果在招生学校公示。海淀区非京籍及按海淀区户籍对待的适龄儿童，须在 规定时间内，持相关材料经居住地所在街道办事处或镇人民政府和相关部门联合审核通过后，按要求取得《学龄人口信息采集表》，随法定监护人到居住地所在学校登记，在区内协调解决。朝阳区申请在朝阳区登记入学的非本市...

赞同0  101浏览  0评论 梁老师 2024-03-10 22:23

文章 2021-2022学年北京东城高三上学期期末数学试卷解析几何解答题解析

[题目](2022，北京东城高三期末，19)已知椭圆C：过点A(-√3,0)，其右焦点为F(1,0)。（Ⅰ）求椭圆C的方程；（Ⅱ）设P为椭圆C上一动点(不在x轴上)，M为AP中点，过原点O作AP的平行 线，与直线x=3交于点Q。问：直线OM与FQ斜率的乘积是否为定值？若为定值，求出该值；若不为定值，请说明理由。 [解析]1）根据已知可得，a=√3，c=1。所以b2=a2-c2=3-1=2。 因此，椭圆C的方程为， 2）方法一：设线法。由于点P不在x轴上，所以直线AP的斜率k≠0，所以设直线AP的方程为：x=ty+√3。与椭圆C的方程联立得，消去x，得到一个关于y的一元二次方程，...

赞同0  142浏览  0评论 梁老师 2024-03-10 22:37

文章 北京各区入学条件不同，一定要分清这些要求，了解清楚，建议收藏

子女、国家或北京市博士后管理部门认定的在京在站博士后研究人员子女、符合随军进京落户条件正在办理随军手续的现役军人子女、父母一方有本市常住户籍或持有《北京市工作居住证》的适龄儿童少年。东城初中入学条件一 、想要在东城区升入初中，需满足下列条件之一：➤本市户籍小学毕业生入学。通过一般初中（优先发展初中）登记入学、全区派位和学区服务片派位安排入学。学生通过北京市初中入学服务系统统一网上填报志愿。对报名人数 少于招生人数的初中，直接入学；对报名人数超过招生人数的初中，随机派位入学，保证每位小学毕业生免试就近升入初中。继续做好九年一贯制直升工作，巩固改革成果，落实定向名额派位入学工作。➤学籍与户口、家庭实际...

赞同0  99浏览  0评论 梁老师 2024-03-10 22:41