AMC10作为美国藤校录取参考竞赛中重要组成部分，AMC10能够拿到竞赛奖项对于申请大学非常有优势。那么在备战AMC10竞赛时，我们需要掌握哪些知识点呢？本文将从几何、代数、概率与统计等方面进行解析

01

AMC10重点知识点梳理

在备战AMC10考试时，我们需要重点掌握以下几个方面的知识：

1. 几何：

包括平面几何和立体几何，其中平面几何占比较大，需要掌握相似三角形、三角形内的点线关系等。

2. 代数：

包括基础代数、函数和三角函数等内容，同余、整除、不定方程，常见函数及其图像 、 高斯函数及其图像、天花板函数及其图像。

3. 概率与统计：

主要涉及概率和统计两个方面的内容，需要掌握古典概率 、几何概型、马尔科夫链、递推。

4. 数论：

虽然数量不多，但是难度较大，也需要多加关注，需要掌握质数、 质因数分解 、因子个数定理、最大公约数、最小公倍数、欧几里得算法。

5. 其他：

如三角形相似、圆锥曲线、排列、组合和分组、 范德蒙恒等式、 容斥原理等内容也需要掌握。

02

必备公式汇总

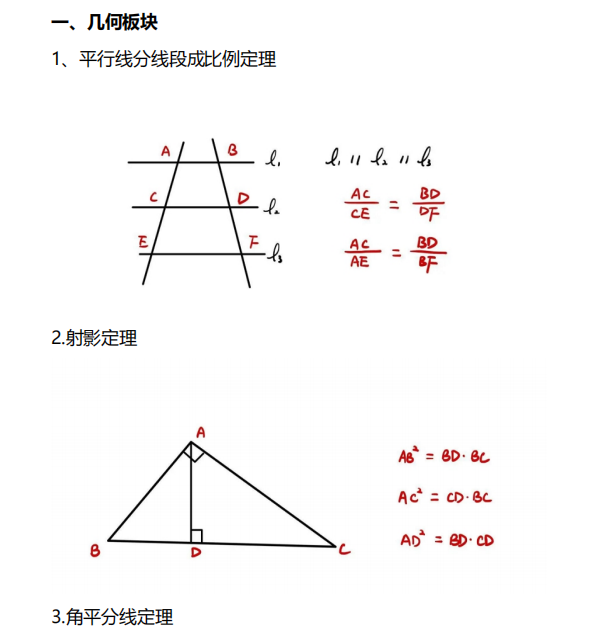
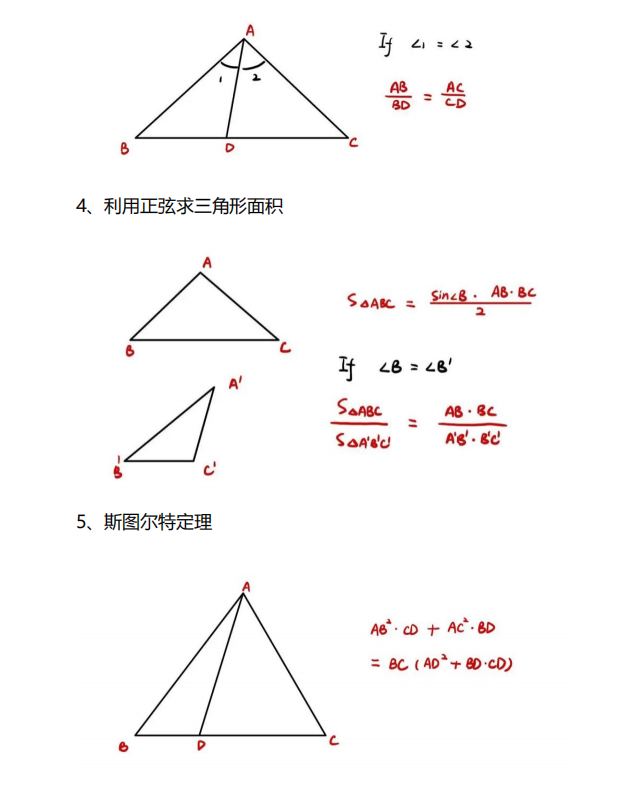
在AMC10考试过程中时间比较紧张，如果学生没有记住常考的公式定理会大大影响答题速度，我们根据历年AMC10考题整理出来AMC10需要掌握的必备公式定理：

以上是一部分AMC10常考知识点汇总

PART 01

几何题型解析

在AMC10考试中，几何题型占比较大。以下是常见的几何题型：

1. 平面几何：

（1）相似三角形；

（2）勾股定理；

（3）正多边形；

（4）圆和圆内接四边形；

（5）直角三角形中高线和中线的性质等。

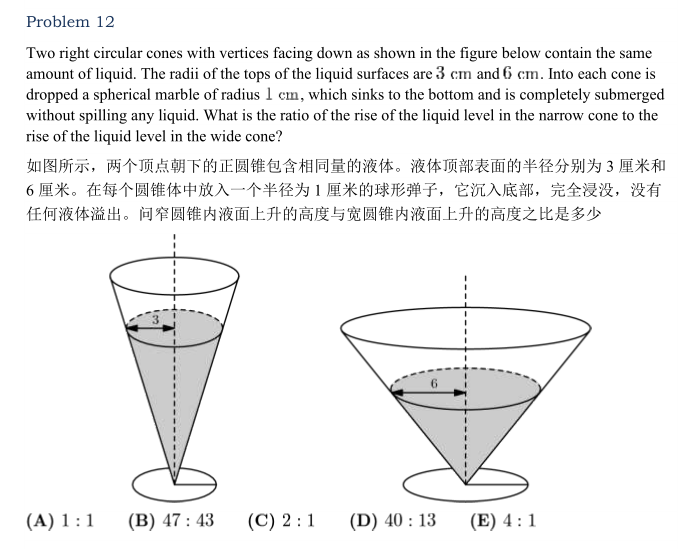
2. 立体几何：

（1）正方体、长方体等基本立体图形；

（2）球和球内接四面体；

（3）棱锥、棱台等复杂立体图形。

PART 02

代数题型解析

除了几何外，代数也是AMC10考试中常见的题型之一。以下是常见的代数题型：

1. 基础代数：

（1）整式加法与乘法；

（2）因式分解；

（3）分式运算；

（4）绝对值与不等式等。

2. 函数：

（1）函数定义域与值域；

（2）函数奇偶性与单调性；

（3）反函数及其性质等。

3. 三角函数：

涉及到正弦、余弦、正切等基本三角函数及其应用。

PART 03

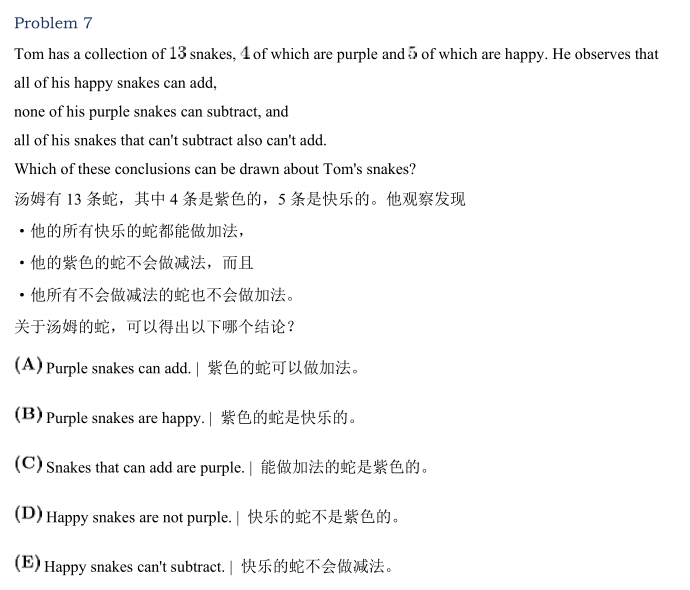
概率与统计题型解析

概率与统计也是AMC10考试中常见的题型之一。

以下是常见的概率与统计题型：

1. 概率问题：主要涉及到事件发生概率、条件概率以及期望值等内容。

2. 统计问题：主要涉及到数据分布特征以及样本均值标准差等内容。