2015年小高组决赛A卷

9. 如果一个自然数的各位数字能够分成两组，使得每组中的数字之和相等，则称这个数为“均衡数”．例如25254是“均衡数”，因为5+2+2=4+5．如果相邻的两个自然数都是“均衡数”，则称这对“均衡数”为“孪生均衡数”．那么最小的一对“孪生均衡数”的和是          ．

〖答案〗1099

11. 三位数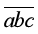除以它的各位数字和的余数是1，三位数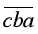除以它的各位数字和的余数也是1．如果不同的字母代表不同的数字，且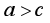，那么＝          ．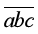

〖答案〗452

2016年小高组决赛A卷

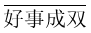9. 四位数除以两位数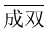的余数恰好为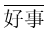；如果不同的汉字表示不同的数字且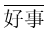和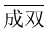不互质，那么四位数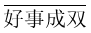最大是__________．

〖答案〗7281

11. 已知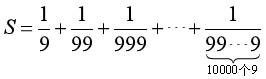，那么S的小数点后第2016位是          ．

〖答案〗6

2017年小高组决赛A卷

7. 有一个四位数，它和6的积是一个完全立方数，它和6的商是一个完全平方数；那么这个四位数是________．

〖答案〗7776

11 .有一列正整数，其中第1个数是1，第2个数是1、2的最小公倍数，第3个数是1、2、3的最小公倍数，……，第n个数是1、2、……、n的最小公倍数．那么这列数的前100个数中共有________个不同的值．

〖答案〗36

2018年小高组决赛A卷

6. 一个五位数由五个互不相同的非零数字组成，、、、依次是6、7、8、9的倍数，且能被6、7、8、9中的两个整除，那么的值是________．

〖答案〗96327

9. 算式的计算结果中有________个奇数数字．

〖答案〗72

2019年小高组决赛A卷

9. 算式中，字母A~I分别表示9个互不相同的非零数字，已知字母C、D、E代表的数字成等比数列，而字母G、H、I代表的数字成等差数列，那么表示的两位数是_________．

〖答案〗25

11. 除以4、9、25的余数之和为17的所有三位数之和除以900的余数是________．
〖答案〗414

点评：数论是国内小学数学竞赛考察的一个重点内容，每年出现在数学花园探秘小高组决赛的数论题一般是两道，主要考察的内容包括整除特征，因数个数，位值原理，完全平方数以及余数问题。

对于常见数的整除特征这里不再赘述，但是同学们一定要牢记；

因数个数的求法是先分解质因数，再把每个质因数的指数（个数）加1再相乘，这里要理解这个方法的原理—其本质是不同质因数的搭配问题，可以用乘法原理解决；

位值原理是解决很多数论问题的利器，我们需要把题目中叙述的具有某些特殊性质的数先用字母表示出来，然后用位值原理进行展开，再去研究这些字母之间的关系；

完全平方数会考察其余数的特征和因数个数的特征；

余数问题主要是求被除数的问题，一般情况我们可以利用转化成和同，差同，余同及逐步满足的方法来解决。

杯赛中的数论问题一般是难度较高的，还可能和计数与数字谜相结合。我们必须要多练习、多思考才能灵活的运用所学知识解决此类问题。